DSP Builder for Intel® FPGAs (Advanced Blockset): Handbook

Download PDF
ID 683337
Date 3/23/2022
Public

A newer version of this document is available. Customers should click here to go to the newest version.

Document Table of Contents
Document Table of Contents x
1. About DSP Builder for Intel® FPGAs 2. DSP Builder for Intel FPGAs Advanced Blockset Getting Started 3. DSP Builder Design Flow 4. Primitive Library Blocks Tutorial 5. IP Tutorial 6. DSP Builder for Intel FPGAs (Advanced Blockset) Design Examples and Reference Designs 7. DSP Builder Design Rules, Design Recommendations, and Troubleshooting 8. About DSP Builder for Intel FPGAs Optimization 9. About Folding 10. Floating-Point Data Types 11. Design Configuration Library 12. IP Library 13. Interfaces Library 14. Primitives Library 15. Utilities Library 16. Simulink Supported Blocks 17. Document Revision History for DSP Builder for Intel FPGAs (Advanced Blockset) Handbook
1. About DSP Builder for Intel® FPGAs x
1.1. DSP Builder for Intel® FPGAs Features 1.2. DSP Builder for Intel® FPGAs Design Structure 1.3. DSP Builder for Intel® FPGAs Libraries 1.4. DSP Builder for Intel® FPGAs Device Support
2. DSP Builder for Intel FPGAs Advanced Blockset Getting Started x
2.1. Starting DSP Builder in MATLAB* 2.2. Browsing DSP Builder Libraries and Adding Blocks to a New Model 2.3. Browsing and Opening DSP Builder Design Examples 2.4. Creating a New DSP Builder Design with the DSP Builder New Model Wizard 2.5. Simulating, Verifying, Generating, and Compiling Your DSP Builder Design
2.4. Creating a New DSP Builder Design with the DSP Builder New Model Wizard x
2.4.1. DSP Builder Menu Options 2.4.2. DSP Builder New Model Wizard Setup Script Parameters
3. DSP Builder Design Flow x
3.1. Implementing your Design in DSP Builder Advanced Blockset 3.2. Verifying your DSP Builder Advanced Blockset Design in Simulink and MATLAB 3.3. Exploring DSP Builder Advanced Blockset Design Tradeoffs 3.4. Verifying your DSP Builder Design with C++ Software Models 3.5. Verifying your DSP Builder Advanced Blockset Design in the ModelSim Simulator 3.6. Verifying Your DSP Builder Design in Hardware 3.7. Integrating Your DSP Builder Advanced Blockset Design into Hardware
3.1. Implementing your Design in DSP Builder Advanced Blockset x
3.1.1. Dividing your DSP Builder Design into Subsystems 3.1.2. Connecting DSP Builder Subsystems 3.1.3. Creating a New Design by Copying a DSP Builder Design Example 3.1.4. Vectorized Inputs
3.1.2. Connecting DSP Builder Subsystems x
3.1.2.1. DSP Builder Block Interface Signals 3.1.2.2. Periods 3.1.2.3. Sample Rate 3.1.2.4. Building Multichannel Systems 3.1.2.5. Channelization for Two Channels with a Folding Factor of 3 3.1.2.6. Channelization for Four Channels with a Folding Factor of 3 3.1.2.7. Synchronization and Scheduling of Data with the Channel Signal 3.1.2.8. Simulink vs Hardware Design Representations
3.1.2.1. DSP Builder Block Interface Signals x
3.1.2.1.1. Multichannel Systems with IP Library Blocks 3.1.2.1.2. Valid, Channel, and Data Examples
3.1.2.4. Building Multichannel Systems x
3.1.2.4.1. Multichannel Systems with IP Library Blocks
3.1.3. Creating a New Design by Copying a DSP Builder Design Example x
3.1.3.1. Creating a New Design From the DSP Builder FIR Design Example and Changing the Namespaces
3.2. Verifying your DSP Builder Advanced Blockset Design in Simulink and MATLAB x
3.2.1. Verifying your DSP Builder Advanced Blockset Design with a Testbench 3.2.2. Running DSP Builder Advanced Blockset Automatic Testbenches 3.2.3. Using DSP Builder Advanced Blockset References 3.2.4. Setting Up Stimulus in DSP Builder Advanced Blockset 3.2.5. Analyzing your DSP Builder Advanced Blockset Design
3.2.1. Verifying your DSP Builder Advanced Blockset Design with a Testbench x
3.2.1.1. Visualization Features
3.2.2. Running DSP Builder Advanced Blockset Automatic Testbenches x
3.2.2.1. The dspba.runModelsimATB Command Syntax 3.2.2.2. Running All Automatic Testbenches 3.2.2.3. The command run_all_atbs Command Syntax 3.2.2.4. Testbench Error Messages
3.3. Exploring DSP Builder Advanced Blockset Design Tradeoffs x
3.3.1. Bit Growth 3.3.2. Managing Bit Growth in DSP Builder Advanced Blockset Designs 3.3.3. Using Rounding and Saturation in DSP Builder Advanced Blockset Designs 3.3.4. Scaling with Primitive Blocks 3.3.5. Changing Data Type with Convert Blocks and Specifying Output Types
3.3.5. Changing Data Type with Convert Blocks and Specifying Output Types x
3.3.5.1. The Convert Block and Real-world Values 3.3.5.2. Output Data Types on Primitive Blocks
3.4. Verifying your DSP Builder Design with C++ Software Models x
3.4.1. Example CMakelist File
3.5. Verifying your DSP Builder Advanced Blockset Design in the ModelSim Simulator x
3.5.1. Automatic Testbench 3.5.2. DSP Builder Advanced Blockset ModelSim Simulations
3.5.1. Automatic Testbench x
3.5.1.1. DSP Builder Advanced Blockset Automatic Testbench Files
3.6. Verifying Your DSP Builder Design in Hardware x
3.6.1. Hardware Verification 3.6.2. Hardware Verification with System-in-the-Loop
3.6.1. Hardware Verification x
3.6.1.1. Hardware Verification Design Example
3.6.2. Hardware Verification with System-in-the-Loop x
3.6.2.1. Preparing for DSP Builder System-In-The-Loop 3.6.2.2. System-In-The-Loop Supported Blocks 3.6.2.3. Building Custom JTAG-Based Board Support Packages 3.6.2.4. Running System-In-the-Loop 3.6.2.5. System-In-The-Loop Parameters
3.6.2.3. Building Custom JTAG-Based Board Support Packages x
3.6.2.3.1. Setting up Board Support Package for 28 nm Device Families 3.6.2.3.2. Setting up Board Support Packages for Other Device Families 3.6.2.3.3. Publishing the Package in the System-In-The-Loop Wizard 3.6.2.3.4. System-in-the-Loop Third-Party Board Support Packages 3.6.2.3.5. Template Values in the System-in-the-Loop boardinfos.xml File
3.7. Integrating Your DSP Builder Advanced Blockset Design into Hardware x
3.7.1. DSP Builder Generated Files 3.7.2. DSP Builder Designs and the Quartus Prime Project 3.7.3. Interfaces with a Processor Bus
3.7.2. DSP Builder Designs and the Quartus Prime Project x
3.7.2.1. Adding a DSP Builder Advanced Blockset Design to an Existing Quartus Prime Project
3.7.3. Interfaces with a Processor Bus x
3.7.3.1. Assigning Base Addresses in DSP Builder Designs 3.7.3.2. Adding a DSP Builder Design to a Platform Designer System 3.7.3.3. Updating Registers with the Nios II Processor
3.7.3.2. Adding a DSP Builder Design to a Platform Designer System x
3.7.3.2.1. Modifying Avalon-ST Blocks 3.7.3.2.2. Restrictions for DSP Builder Designs with Avalon Streaming Interface Blocks
4. Primitive Library Blocks Tutorial x
4.1. Creating a Fibonacci Design from the DSP Builder Primitive Library 4.2. Setting the Parameters on the Testbench Source Blocks 4.3. Simulating the Fibonacci Design in Simulink 4.4. Modifying the DSP Builder Fibonacci Design to Generate Vector Signals 4.5. Simulating the RTL of the Fibonacci Design
5. IP Tutorial x
5.1. Creating an IP Design 5.2. Simulating the IP Design in Simulink 5.3. Viewing Timing Closure and Viewing Resource Utilization for the DSP Builder IP Design 5.4. Reparameterizing the DSP Builder FIR Filter to Double the Number of Channels 5.5. Doubling the Target Clock Rate for a DSP Builder IP Design
6. DSP Builder for Intel FPGAs (Advanced Blockset) Design Examples and Reference Designs x
6.1. DSP Builder Design Configuration Block Design Examples 6.2. DSP Builder FFT Design Examples 6.3. DSP Builder DDC Design Example 6.4. DSP Builder Filter Design Examples 6.5. DSP Builder Finite State Machine Design Example 6.6. DSP Builder Folding Design Examples 6.7. DSP Builder Floating Point Design Examples 6.8. DSP Builder Flow Control Design Examples 6.9. DSP Builder HDL Import Design Example 6.10. DSP Builder Host Interface Design Examples 6.11. DSP Builder Platform Design Examples 6.12. DSP Builder Primitive Block Design Examples 6.13. DSP Builder Reference Designs 6.14. DSP Builder Waveform Synthesis Design Examples
6.1. DSP Builder Design Configuration Block Design Examples x
6.1.1. Scale 6.1.2. Local Threshold
6.2. DSP Builder FFT Design Examples x
6.2.1. FFT 6.2.2. FFT without BitReverseCoreC Block 6.2.3. IFFT 6.2.4. IFFT without BitReverseCoreC Block 6.2.5. Floating-Point FFT 6.2.6. Floating-Point FFT without BitReverseCoreC Block 6.2.7. Floating-Point iFFT 6.2.8. Floating-Point iFFT without BitReverseCoreC Block 6.2.9. Multichannel FFT 6.2.10. Multiwire Transpose 6.2.11. Parallel FFT 6.2.12. Parallel Floating-Point FFT 6.2.13. Single-Wire Transpose 6.2.14. Switchable FFT/iFFT 6.2.15. Variable-Size Fixed-Point FFT 6.2.16. Variable-Size Fixed-Point FFT without BitReverseCoreC Block 6.2.17. Variable-Size Fixed-Point iFFT 6.2.18. Variable-Size Fixed-Point iFFT without BitReverseCoreC Block 6.2.19. Variable-Size Floating-Point FFT 6.2.20. Variable-Size Floating-Point FFT without BitReverseCoreC Block 6.2.21. Variable-Size Floating-Point iFFT 6.2.22. Variable-Size Floating-Point iFFT without BitReverseCoreC Block 6.2.23. Variable-Size Low-Resource FFT 6.2.24. Variable-Size Low-Resource Real-Time FFT 6.2.25. Variable-Size Supersampled FFT
6.3. DSP Builder DDC Design Example x
6.3.1. DDC Design Example Subsystem 6.3.2. Building the DDC Design Example
6.3.2. Building the DDC Design Example x
6.3.2.1. DDC Design Example Generated Files
6.4. DSP Builder Filter Design Examples x
6.4.1. Complex FIR Filter 6.4.2. Decimating CIC Filter 6.4.3. Decimating FIR Filter 6.4.4. Filter Chain with Forward Flow Control 6.4.5. FIR Filter with Exposed Bus 6.4.6. Fractional FIR Filter Chain 6.4.7. Fractional-Rate FIR Filter 6.4.8. Half-Band FIR Filter 6.4.9. IIR: Full-rate Fixed-point 6.4.10. IIR: Full-rate Floating-point 6.4.11. Interpolating CIC Filter 6.4.12. Interpolating FIR Filter 6.4.13. Interpolating FIR Filter with Multiple Coefficient Banks 6.4.14. Interpolating FIR Filter with Updating Coefficient Banks 6.4.15. Root-Raised Cosine FIR Filter 6.4.16. Single-Rate FIR Filter 6.4.17. Super-Sample Decimating FIR Filter 6.4.18. Super-Sample Fractional FIR Filter 6.4.19. Super-Sample Interpolating FIR Filter 6.4.20. Variable-Rate CIC Filter
6.6. DSP Builder Folding Design Examples x
6.6.1. Position, Speed, and Current Control for AC Motors 6.6.2. Position, Speed, and Current Control for AC Motors (with ALU Folding) 6.6.3. About FOC 6.6.4. Folded FIR Filter
6.7. DSP Builder Floating Point Design Examples x
6.7.1. Black-Scholes Floating Point 6.7.2. Double-Precision Real Floating-Point Matrix Multiply 6.7.3. Fine Doppler Estimator 6.7.4. Floating-Point Mandlebrot Set 6.7.5. General Real Matrix Multiply One Cycle Per Output 6.7.6. Newton Root Finding Tutorial Step 1—Iteration 6.7.7. Newton Root Finding Tutorial Step 2—Convergence 6.7.8. Newton Root Finding Tutorial Step 3—Valid 6.7.9. Newton Root Finding Tutorial Step 4—Control 6.7.10. Newton Root Finding Tutorial Step 5—Final 6.7.11. Normalizer 6.7.12. Single-Precision Complex Floating-Point Matrix Multiply 6.7.13. Single-Precision Real Floating-Point Matrix Multiply 6.7.14. Simple Nonadaptive 2D Beamformer
6.8. DSP Builder Flow Control Design Examples x
6.8.1. Avalon-ST Interface (Input and Output FIFO Buffer) with Backpressure 6.8.2. Avalon-ST Interface (Output FIFO Buffer) with Backpressure 6.8.3. Kronecker Tensor Product 6.8.4. Parallel Loops 6.8.5. Primitive FIR with Back Pressure 6.8.6. Primitive FIR with Forward Pressure 6.8.7. Primitive Systolic FIR with Forward Flow Control 6.8.8. Rectangular Nested Loop 6.8.9. Sequential Loops 6.8.10. Triangular Nested Loop
6.9. DSP Builder HDL Import Design Example x
VHDL Components Top-Level Design Digital Up Converter Buffer and Upsample Mixer Scale FIR Coefficients DPD Simulink Simulations Results 6.9.1. Performing a Cosimulation
6.10. DSP Builder Host Interface Design Examples x
6.10.1. Memory-Mapped Registers
6.11. DSP Builder Platform Design Examples x
6.11.1. 16-Channel DDC 6.11.2. 16-Channel DUC 6.11.3. 2-Antenna DUC for WiMAX 6.11.4. 2-Channel DUC 6.11.5. Super-Sample Rate Digital Upconverter
6.12. DSP Builder Primitive Block Design Examples x
6.12.1. 8×8 Inverse Discrete Cosine Transform 6.12.2. Automatic Gain Control 6.12.3. Bit Combine for Boolean Vectors 6.12.4. Bit Extract for Boolean Vectors 6.12.5. Color Space Converter 6.12.6. CORDIC from Primitive Blocks 6.12.7. Digital Predistortion Forward Path 6.12.8. Fibonacci Series 6.12.9. Folded Vector Sort 6.12.10. Fractional Square Root Using CORDIC 6.12.11. Fixed-point Maths Functions 6.12.12. Gaussian Random Number Generator 6.12.13. Hello World 6.12.14. Hybrid Direct Form and Transpose Form FIR Filter 6.12.15. Loadable Counter 6.12.16. Matrix Initialization of LUT 6.12.17. Matrix Initialization of Vector Memories 6.12.18. Multichannel IIR Filter 6.12.19. Quadrature Amplitude Modulation 6.12.20. Reinterpret Cast for Bit Packing and Unpacking 6.12.21. Run-time Configurable Decimating and Interpolating Half-Rate FIR Filter 6.12.22. Square Root Using CORDIC 6.12.23. Test CORDIC Functions with the CORDIC Block 6.12.24. Uniform Random Number Generator 6.12.25. Vector Sort—Sequential 6.12.26. Vector Sort—Iterative 6.12.27. Vector Initialization of Sample Delay 6.12.28. Wide Single-Channel Accumulators
6.13. DSP Builder Reference Designs x
6.13.1. 1-Antenna WiMAX DDC 6.13.2. 2-Antenna WiMAX DDC 6.13.3. 1-Antenna WiMAX DUC 6.13.4. 2-Antenna WiMAX DUC 6.13.5. 4-Carrier, 2-Antenna W-CDMA DDC 6.13.6. 1-Carrier, 2-Antenna W-CDMA DDC 6.13.7. 4-Carrier, 2-Antenna W-CDMA DUC 6.13.8. 4-Carrier, 4-Antenna DUC and DDC for LTE 6.13.9. 1-Carrier, 2-Antenna W-CDMA DDC 6.13.10. 4-Carrier, 2-Antenna High-Speed W-CDMA DUC at 368.64 MHz with Total Rate Change 32 6.13.11. 4-Carrier, 2-Antenna High-Speed W-CDMA DUC at 368.64 MHz with Total Rate Change 48 6.13.12. 4-Carrier, 2-Antenna High-Speed W-CDMA DUC at 307.2 MHz with Total Rate Change 40 6.13.13. Cholesky-based Matrix Inversion 6.13.14. Cholesky Solver Multiple Channels 6.13.15. Crest Factor Reduction 6.13.16. Direct RF with Synthesizable Testbench 6.13.17. Dynamic Decimating FIR Filter 6.13.18. Multichannel QR Decompostion 6.13.19. QR Decompostion 6.13.20. QRD Solver 6.13.21. Reconfigurable Decimation Filter 6.13.22. Single-Channel 10-MHz LTE Transmitter 6.13.23. STAP Radar Forward and Backward Substitution 6.13.24. STAP Radar Steering Generation 6.13.25. STAP Radar QR Decomposition 192x204 6.13.26. Time Delay Beamformer 6.13.27. Transmit and Receive Modem 6.13.28. Variable Integer Rate Decimation Filter
6.14. DSP Builder Waveform Synthesis Design Examples x
6.14.1. Complex Mixer 6.14.2. Four Channel, Two Banks NCO 6.14.3. Four Channel, Four Banks NCO 6.14.4. Four Channel, Eight Banks, Two Wires NCO 6.14.5. Four Channel, 16 Banks NCO 6.14.6. IP 6.14.7. NCO 6.14.8. NCO with Exposed Bus 6.14.9. Real Mixer 6.14.10. Super-sample NCO
7. DSP Builder Design Rules, Design Recommendations, and Troubleshooting x
7.1. DSP Builder Design Rules and Recommendations 7.2. Troubleshooting DSP Builder Designs
7.2. Troubleshooting DSP Builder Designs x
7.2.1. About Loops 7.2.2. DSP Builder Timed Feedback Loops 7.2.3. DSP Builder Loops, Clock Cycles, and Data Cycles
8. About DSP Builder for Intel FPGAs Optimization x
8.1. Associating DSP Builder with MATLAB 8.2. Setting Up Simulink for DSP Builder Designs 8.3. The DSP Builder Windows Shortcut 8.4. Setting DSP Builder Design Parameters with MATLAB Scripts 8.5. Managing your Designs 8.6. How to Manage Latency 8.7. Flow Control in DSP Builder Designs 8.8. Reset Minimization 8.9. About Importing HDL
8.2. Setting Up Simulink for DSP Builder Designs x
8.2.1. Setting Up Simulink Solver 8.2.2. Setting Up Simulink Signal Display Option
8.4. Setting DSP Builder Design Parameters with MATLAB Scripts x
8.4.1. Running Setup Scripts Automatically 8.4.2. Defining Unique DSP Builder Design Parameters 8.4.3. Example DSP Builder Custom Scripts
8.5. Managing your Designs x
8.5.1. Managing Basic Parameters 8.5.2. Creating User Libraries and Converting a Primitive Subsystem into a Custom Block 8.5.3. Revision Control
8.6. How to Manage Latency x
8.6.1. Reading the Added Latency Value for an IP Block 8.6.2. Zero Latency Example 8.6.3. Implicit Delays in DSP Builder Designs 8.6.4. Distributed Delays in DSP Builder Designs 8.6.5. Latency and fMAX Constraint Conflicts in DSP Builder Designs 8.6.6. Control Units Delays
9. About Folding x
9.1. ALU Folding 9.2. Removing Resource Sharing Folding
9.1. ALU Folding x
9.1.1. ALU Folding Limitations 9.1.2. ALU Folding Parameters 9.1.3. ALU Folding Simulation Rate 9.1.4. Using ALU Folding 9.1.5. Using Automated Verification 9.1.6. Ready Signal 9.1.7. Connecting the ALU Folding Ready Signal 9.1.8. About the ALU Folding Start of Packet Signal
10. Floating-Point Data Types x
10.1. DSP Builder Floating-Point Data Type Features 10.2. DSP Builder Supported Floating-Point Data Types 10.3. DSP Builder Round-Off Errors 10.4. Trading Off Logic Utilization and Accuracy in DSP Builder Designs 10.5. Upgrading Pre v14.0 Designs 10.6. Floating-Point Sine Wave Generator Tutorial 10.7. Newton-Raphson Root Finding Tutorial 10.8. Forcing Soft Floating-point Data Types with the Advanced Options
10.6. Floating-Point Sine Wave Generator Tutorial x
10.6.1. Creating a Sine Wave Generator in DSP Builder 10.6.2. Using Data Type Variables to Parameterize Designs 10.6.3. Using Data-Type Propagation in DSP Builder Designs 10.6.4. DSP Builder Testbench Verification
10.6.4. DSP Builder Testbench Verification x
10.6.4.1. Tuning ATB Thresholds 10.6.4.2. Writing Application Specific Verification 10.6.4.3. Performing Bit-Accurate Simulation 10.6.4.4. Adder Trees and Scalar Products 10.6.4.5. Creating Floating-Point Accumulators for Designs that Use Iteration
10.7. Newton-Raphson Root Finding Tutorial x
10.7.1. Implementing the Newton Design 10.7.2. Improving DSP Builder Floating-Point Designs
11. Design Configuration Library x
11.1. Avalon Memory-Mapped Agent Settings (AvalonMemoryMappedAgentSettings) 11.2. Control 11.3. Device 11.4. Edit Params 11.5. LocalThreshold
11.2. Control x
11.2.1. DSP Builder Memory and Multiplier Trade-Off Options
12. IP Library x
12.1. Channel Filter and Waveform Library 12.2. Dependent Delay Library 12.3. FFT IP Library
12.1. Channel Filter and Waveform Library x
12.1.1. DSP Builder FIR and CIC Filters 12.1.2. DSP Builder FIR Filters 12.1.3. Channel Viewer (ChanView) 12.1.4. Complex Mixer (ComplexMixer) 12.1.5. Decimating CIC 12.1.6. Decimating FIR 12.1.7. Fractional Rate FIR 12.1.8. Interpolating CIC 12.1.9. Interpolating FIR 12.1.10. NCO 12.1.11. Real Mixer (Mixer) 12.1.12. Scale 12.1.13. Single-Rate FIR
12.1.1. DSP Builder FIR and CIC Filters x
12.1.1.1. Common CIC and FIR Filter Features 12.1.1.2. Updated Help 12.1.1.3. Half-Band and L-Band Nyquist FIR Filters 12.1.1.4. Parameterization of CIC and FIR Filters 12.1.1.5. Setting and Changing FIR Filter Coefficients at Runtime in DSP Builder
12.1.2. DSP Builder FIR Filters x
12.1.2.1. FIR Filter Avalon-MM Interfaces 12.1.2.2. Reconfigurable FIR Filters
12.1.10. NCO x
12.1.10.1. NCO Block Phase Increment and Inversion 12.1.10.2. NCO Block Phase Increment Memory Registers 12.1.10.3. NCO Block Frequency Hopping
12.3. FFT IP Library x
12.3.1. Bit Reverse Core C (BitReverseCoreC and VariableBitReverse) 12.3.2. FFT (FFT, FFT_Light, VFFT, VFFT_Light)
13. Interfaces Library x
13.1. Memory-Mapped Library 13.2. Streaming Library
13.1. Memory-Mapped Library x
13.1.1. Bus Slave (BusSlave) 13.1.2. Bus Stimulus (BusStimulus) 13.1.3. Bus Stimulus File Reader (Bus StimulusFileReader) 13.1.4. External Memory, Memory Read, Memory Write 13.1.5. Register Bit (RegBit) 13.1.6. Register Field (RegField) 13.1.7. Register Out (RegOut) 13.1.8. Shared Memory (SharedMem)
13.2. Streaming Library x
13.2.1. Avalon-ST Input (AStInput) 13.2.2. Avalon-ST Input FIFO Buffer (AStInputFIFO) 13.2.3. Avalon-ST Output (AStOutput)
14. Primitives Library x
14.1. Vector and Complex Type Support 14.2. DFT Design Elements Library 14.3. FFT Design Elements Library 14.4. Primitive Basic Blocks Library 14.5. Primitive Configuration Library 14.6. Primitive Design Elements Library
14.1. Vector and Complex Type Support x
14.1.1. Vector Type Support 14.1.2. Complex Support
14.1.1. Vector Type Support x
14.1.1.1. Element by Element Mode 14.1.1.2. Mathematical Vector Mode 14.1.1.3. Interactions with Simulink
14.1.2. Complex Support x
14.1.2.1. Interactions with Simulink
14.2. DFT Design Elements Library x
14.2.1. DFT (DFT) 14.2.2. Reorder (ReorderBlock) 14.2.3. Reorder and Rescale (ReorderAndRescale)
14.3. FFT Design Elements Library x
14.3.1. About Pruning and Twiddle for FFT Blocks 14.3.2. Bit Vector Combine (BitVectorCombine) 14.3.3. Butterfly Unit (BFU) 14.3.4. Butterfly I C (BFIC) (Deprecated) 14.3.5. Butterfly II C (BFIIC) (Deprecated) 14.3.6. Choose Bits (ChooseBits) 14.3.7. Crossover Switch (XSwitch) 14.3.8. Dual Twiddle Memory (DualTwiddleMemoryC) 14.3.9. Edge Detect (EdgeDetect) 14.3.10. Floating-Point Twiddle Generator (TwiddleGenF) (Deprecated) 14.3.11. Fully-Parallel FFTs (FFT2P, FFT4P, FFT8P, FFT16P, FFT32P, and FFT64P) 14.3.12. Fully-Parallel FFTs with Flexible Ordering (FFT2X, FFT4X, FFT8X, FFT16X, FFT32X, and FFT64X) 14.3.13. General Multitwiddle and General Twiddle (GeneralMultiTwiddle, GeneralMultVTwiddle, GeneralTwiddle, GeneralVTwiddle) 14.3.14. Hybrid FFT (Hybrid_FFT, HybridVFFT) 14.3.15. Multiwire Transpose (MultiwireTranspose) 14.3.16. Parallel Pipelined FFT (PFFT_Pipe) 14.3.17. Pulse Divider (PulseDivider) 14.3.18. Pulse Multiplier (PulseMultiplier) 14.3.19. Single-Wire Transpose (Transpose) 14.3.20. Split Scalar (SplitScalar) 14.3.21. Streaming FFTs (FFT2, FFT4, VFFT2, and VFFT4) 14.3.22. Stretch Pulse (StretchPulse) 14.3.23. Twiddle Angle (TwiddleAngle) 14.3.24. Twiddle Generator (TwiddleGenC) Deprecated 14.3.25. Twiddle and Variable Twiddle (Twiddle and VTwiddle) 14.3.26. Twiddle ROM (TwiddleRom, TwiddleMultRom and TwiddleRomF (deprecated))
14.4. Primitive Basic Blocks Library x
14.4.1. Absolute Value (Abs) 14.4.2. Accumulator (Acc) 14.4.3. Add 14.4.4. Add SLoad (AddSLoad) 14.4.5. AddSub 14.4.6. AddSubFused 14.4.7. AND Gate (And) 14.4.8. Bit Combine (BitCombine) 14.4.9. Bit Extract (BitExtract) 14.4.10. Bit Reverse (BitReverse) 14.4.11. Compare (CmpCtrl) 14.4.12. Complex Conjugate (ComplexConjugate) 14.4.13. Compare Equality (CmpEQ) 14.4.14. Compare Greater Than (CmpGE) 14.4.15. Compare Less Than (CmpLT) 14.4.16. Compare Not Equal (CmpNE) 14.4.17. Constant (Const) 14.4.18. Constant Multiply (Const Mult) 14.4.19. Convert 14.4.20. CORDIC 14.4.21. Counter 14.4.22. Count Leading Zeros, Ones, or Sign Bits (CLZ) 14.4.23. Dual Memory (DualMem) 14.4.24. Demultiplexer (Demux) 14.4.25. Divide 14.4.26. Fanout 14.4.27. FIFO 14.4.28. Floating-point Classifier (FloatClass) 14.4.29. Floating-point Multiply Accumulate (MultAcc) 14.4.30. ForLoop 14.4.31. Load Exponent (LdExp) 14.4.32. Left Shift (LShift) 14.4.33. Loadable Counter (LoadableCounter) 14.4.34. Look-Up Table (Lut) 14.4.35. Loop 14.4.36. Math 14.4.37. Minimum and Maximum (MinMax) 14.4.38. MinMaxCtrl 14.4.39. Multiply (Mult) 14.4.40. Multiplexer (Mux) 14.4.41. NAND Gate (Nand) 14.4.42. Negate 14.4.43. NOR Gate (Nor) 14.4.44. NOT Gate (Not) 14.4.45. OR Gate (Or) 14.4.46. Polynomial 14.4.47. Ready 14.4.48. Reinterpret Cast (ReinterpretCast) 14.4.49. Round 14.4.50. Sample Delay (SampleDelay) 14.4.51. Scalar Product 14.4.52. Select 14.4.53. Sequence 14.4.54. Shift 14.4.55. Sqrt 14.4.56. Subtract (Sub) 14.4.57. Sum of Elements (SumOfElements) 14.4.58. Trig 14.4.59. XNOR Gate (Xnor) 14.4.60. XOR Gate (Xor)
14.5. Primitive Configuration Library x
14.5.1. Channel In (ChannelIn) 14.5.2. Channel Out (ChannelOut) 14.5.3. General Purpose Input (GPIn) 14.5.4. General Purpose Output (GPOut) 14.5.5. Synthesis Information (SynthesisInfo)
14.5.5. Synthesis Information (SynthesisInfo) x
14.5.5.1. Scheduled Synthesis 14.5.5.2. Updated Help
14.6. Primitive Design Elements Library x
14.6.1. Anchored Delay 14.6.2. Complex to Real-Imag 14.6.3. Enabled Delay Line 14.6.4. Enabled Feedback Delay 14.6.5. Expand Scalar (ExpandScalar) 14.6.6. Finite State Machine 14.6.7. Nested Loops (NestedLoop1, NestedLoop2, NestedLoop3) 14.6.8. Pause 14.6.9. Reset-Priority Latch (SRlatch_PS) 14.6.10. Same Data Type (SameDT) 14.6.11. Set-Priority Latch (SRlatch) 14.6.12. Single-Cycle Latency Latch (latch_1L) 14.6.13. Tapped Line Delay (TappedLineDelay) 14.6.14. Variable Super-Sample Delay (VariableDelay) 14.6.15. Vector Fanout (VectorFanout) 14.6.16. Vector Multiplexer (VectorMux) 14.6.17. Zero-Latency Latch (latch_0L)
15. Utilities Library x
15.1. Analyze and Test Library
15.1. Analyze and Test Library x
15.1.1. Capture Values 15.1.2. HDL Import 15.1.3. HDL Import Config 15.1.4. Pause
1. About DSP Builder for Intel® FPGAs
2. DSP Builder for Intel FPGAs Advanced Blockset Getting Started
3. DSP Builder Design Flow
4. Primitive Library Blocks Tutorial
5. IP Tutorial
6. DSP Builder for Intel FPGAs (Advanced Blockset) Design Examples and Reference Designs
7. DSP Builder Design Rules, Design Recommendations, and Troubleshooting
8. About DSP Builder for Intel FPGAs Optimization
9. About Folding
10. Floating-Point Data Types
11. Design Configuration Library
12. IP Library
13. Interfaces Library
14. Primitives Library
15. Utilities Library
16. Simulink Supported Blocks
17. Document Revision History for DSP Builder for Intel FPGAs (Advanced Blockset) Handbook

6.9. DSP Builder HDL Import Design Example

This digital up-converter resamples 20 MSPS complex base-band data to 80 MHz intermediate frequency, mixes it to center on +25 MHz, and applies some simple digital predistortion (DPD). This design example takes FIR and DPD VHDL components to create a complete up-conversion chain by importing existing IP and adding the up-conversion, mixer and pre-DPD scaling.

The digital upconverter includes: input memory, upconverter, FIR filter, scaler, mixer and digital predistortion (DPD).

Table 18.  Example Design Files
hdl_import_duc.mdl The DSP Builder design.
hdl_import_duc_params.xml The design's parameter file.
hdl_import_calc_fir_coefs.m A script to generate the FIR coefficients using MATLAB's cfirpm function. DSP Builder prints the coefficients to MATLAB's Command Window and you can copy and paste them into coefficients.vhd.
calc_dpd_coefs.m A script to generate the DPD coefficients using a simple polynomial model of a power amplifier. DSP Builder prints the coefficients MATLAB's Command Window and you can copy and paste them into lut_dpd.vhd.
to_import This directory contains 12 VHDL source files.

VHDL Components

The design example includes a complex FIR filter in VHDL optimized for Intel Stratix 10 devices. This FIR filter has one valid data sample every eight clock cycles.

See Designing Filters for High Performance.

The simple LUT-based DPD is initialized with a third-order polynomial.

Top-Level Design

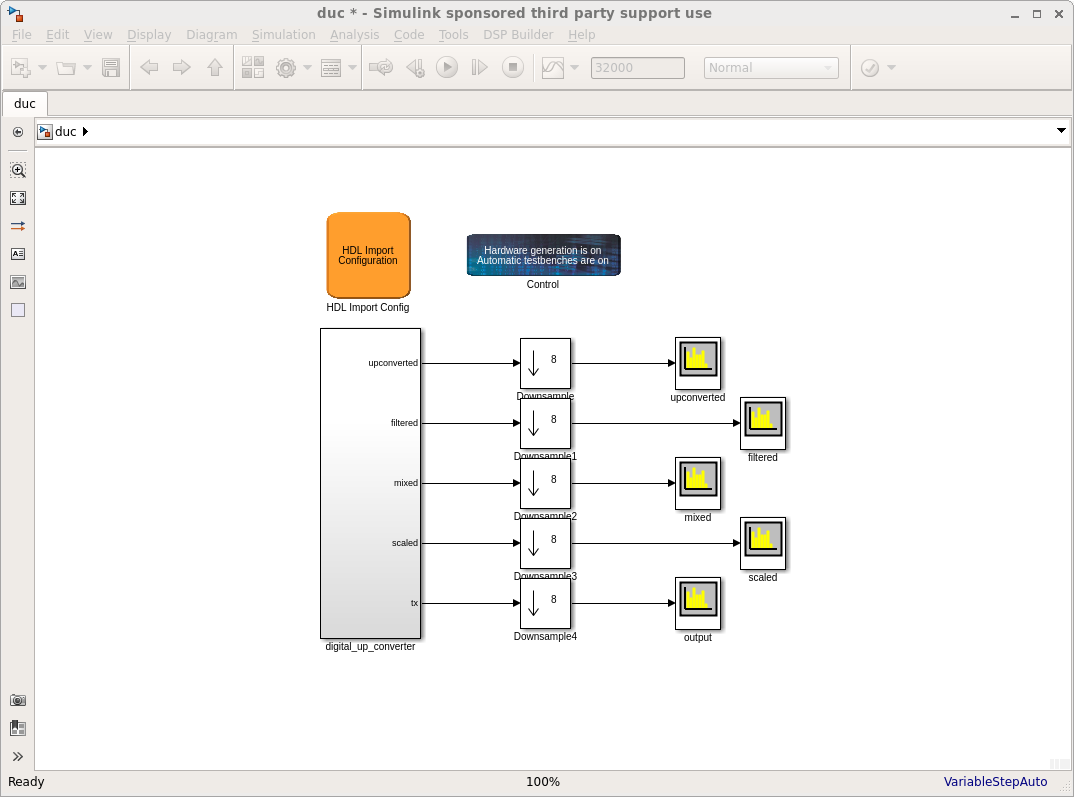
The top-level design contains the device-level subsystem and five downsample and spectrum analyzer blocks from MathWork's DSP System Toolbox. These blocks show the spectral output from the various stages of the up-conversion chain.

Figure 53. Top-Level Design

Digital Up Converter

The digital_up_converter subsystem is the device-level subsystem. It contains all of the design's DSP Builder-based components and two gaps for HDL Import blocks.

Figure 54. Digital Upconverter

Buffer and Upsample

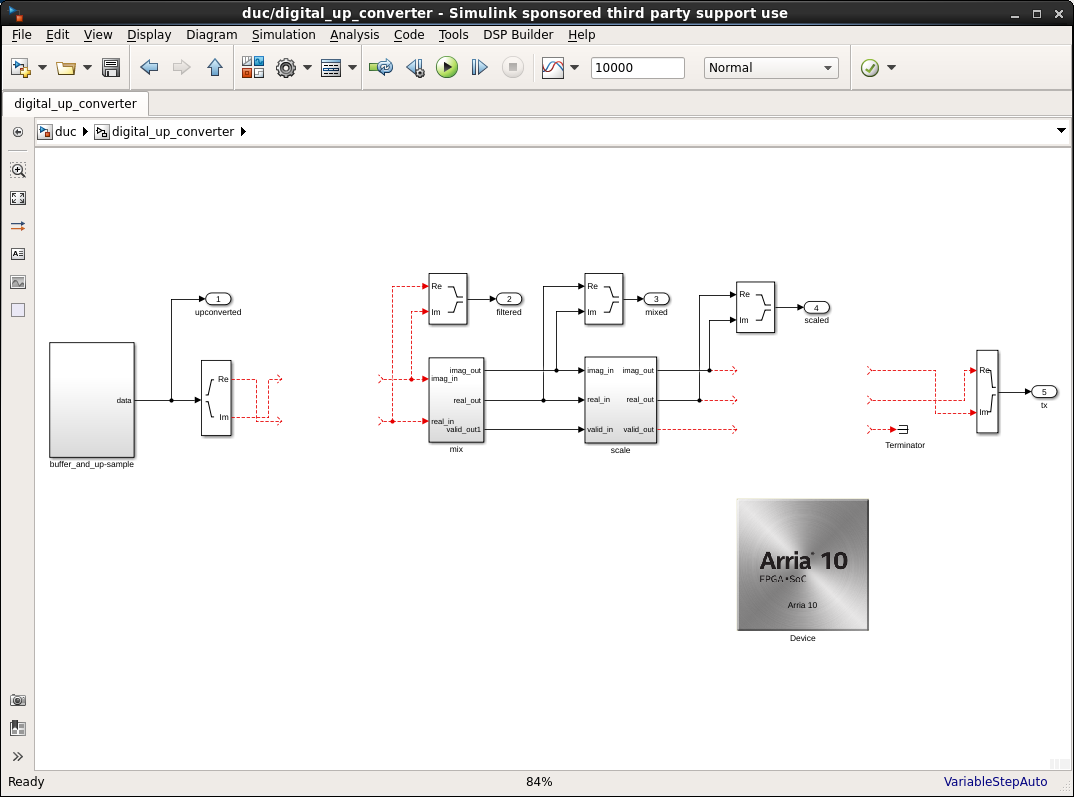
This scheduled subsystem contains two SharedMem blocks, which contain the 20 MSPS baseband source: one for the real part of the signal and one for the imaginary part. You can write to the blocks via the bus or use the preloaded tones.

The read_counter block drives the upconversion. It counts modulo 32 because it upsamples the 20 MSPS baseband by 4 to 80 MSPS and then holds each sample for 8 clock cycles at a clock rate of 640 MHz. The FIR filter accepts one sample every eight cycles. By holding the samples, the FIR does not need synchronization logic.

Figure 55. Buffer and Up-Sample

Mixer

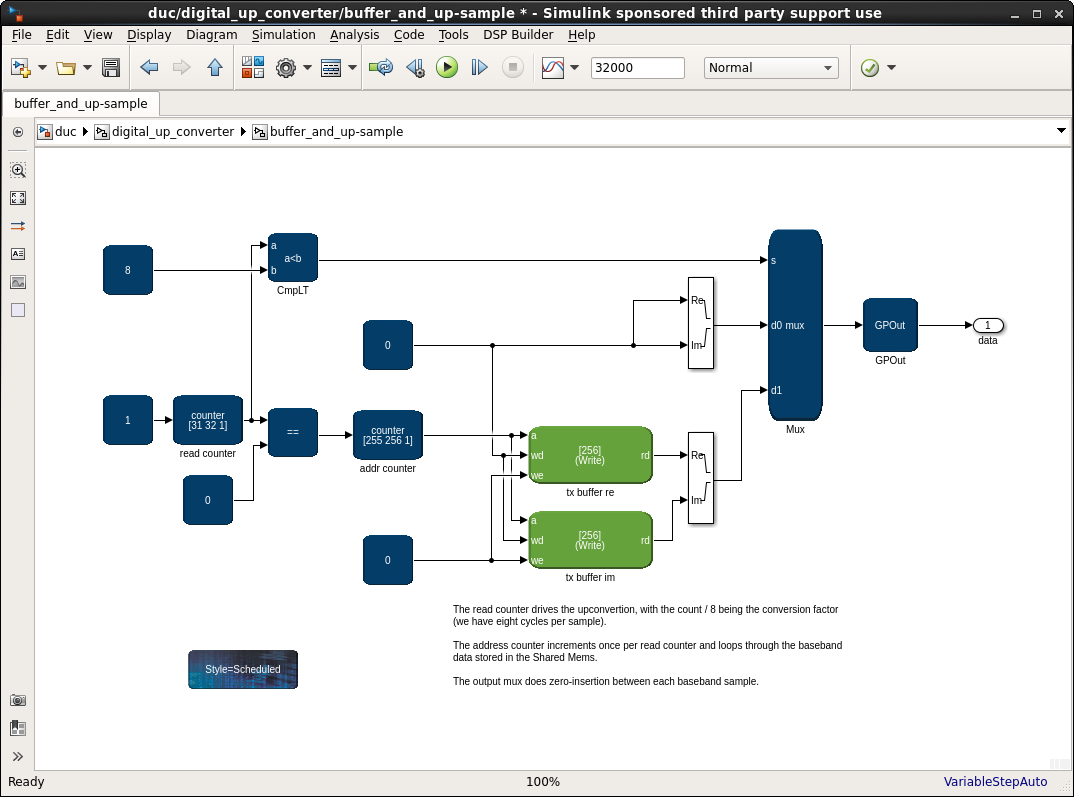
This single-channel mixer consists of NCO and ComplexMixer IP blocks and a scheduled subsystem for controlling the NCO. The control subsystem asserts the valid signal once every eight cycles. The NCO generates a 16 MHz complex tone, which the ComplexMixer uses to mix the filtered signal.

Figure 56. Mixer

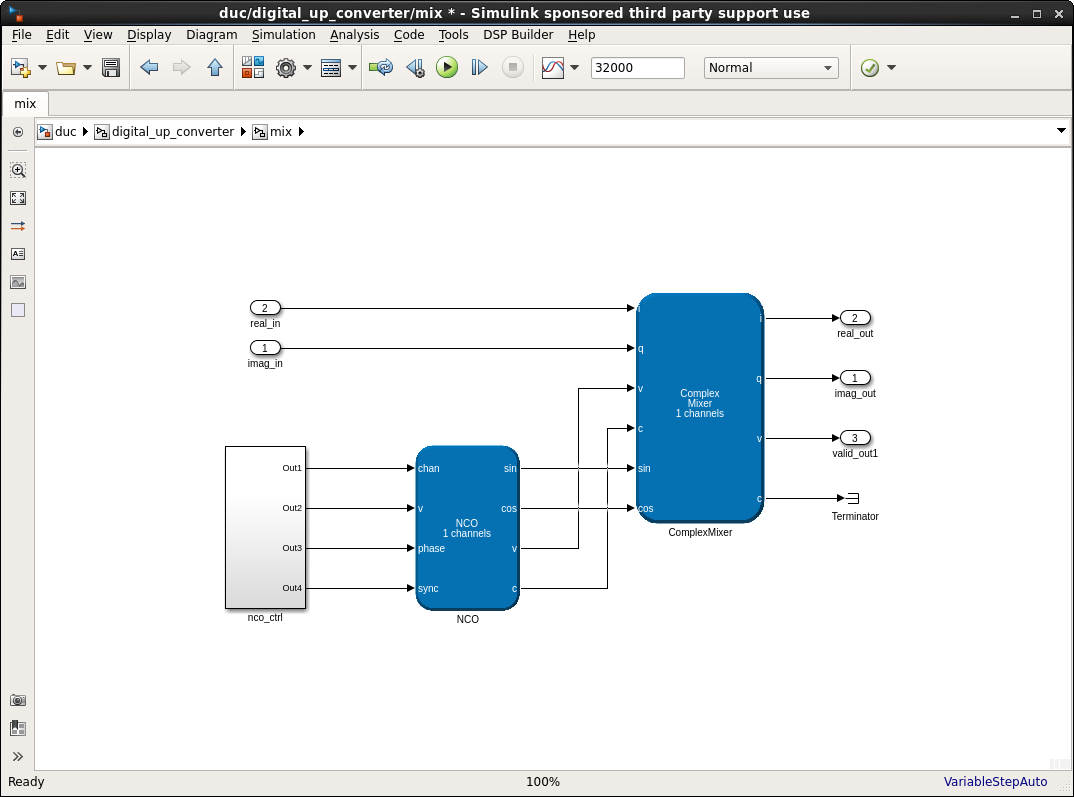
Scale

The scale scheduled subsystem scales the data so that it fits within the DPD's range of operation by bit-shifting from the mixer's output. You can use the optional multiplier for increasing the signal level if bit-shifting is insufficient.

Figure 57. Scale

FIR Coefficients

The FIR coefficients are defined in coefficients.vhd.

The coefficients are calculated in hdl_import_calc_fir_coefs.m. This script uses MATLAB’s cfirpm command to create complex coefficients.

DPD

The file lut_dpd.vhd contains the DPD for this design example. The DPD consists of an address generator that indexes a LUT. The output of the LUT is then multiplied with the complex input data. The LUT contents are calculated in hdl_import_calc_dpd_coefs.m. This script uses a simple, real-numbered, third-order model of an amplifier to calculate predistortion coefficients. DSP Builder uses these coefficients to calculate the LUT contents.

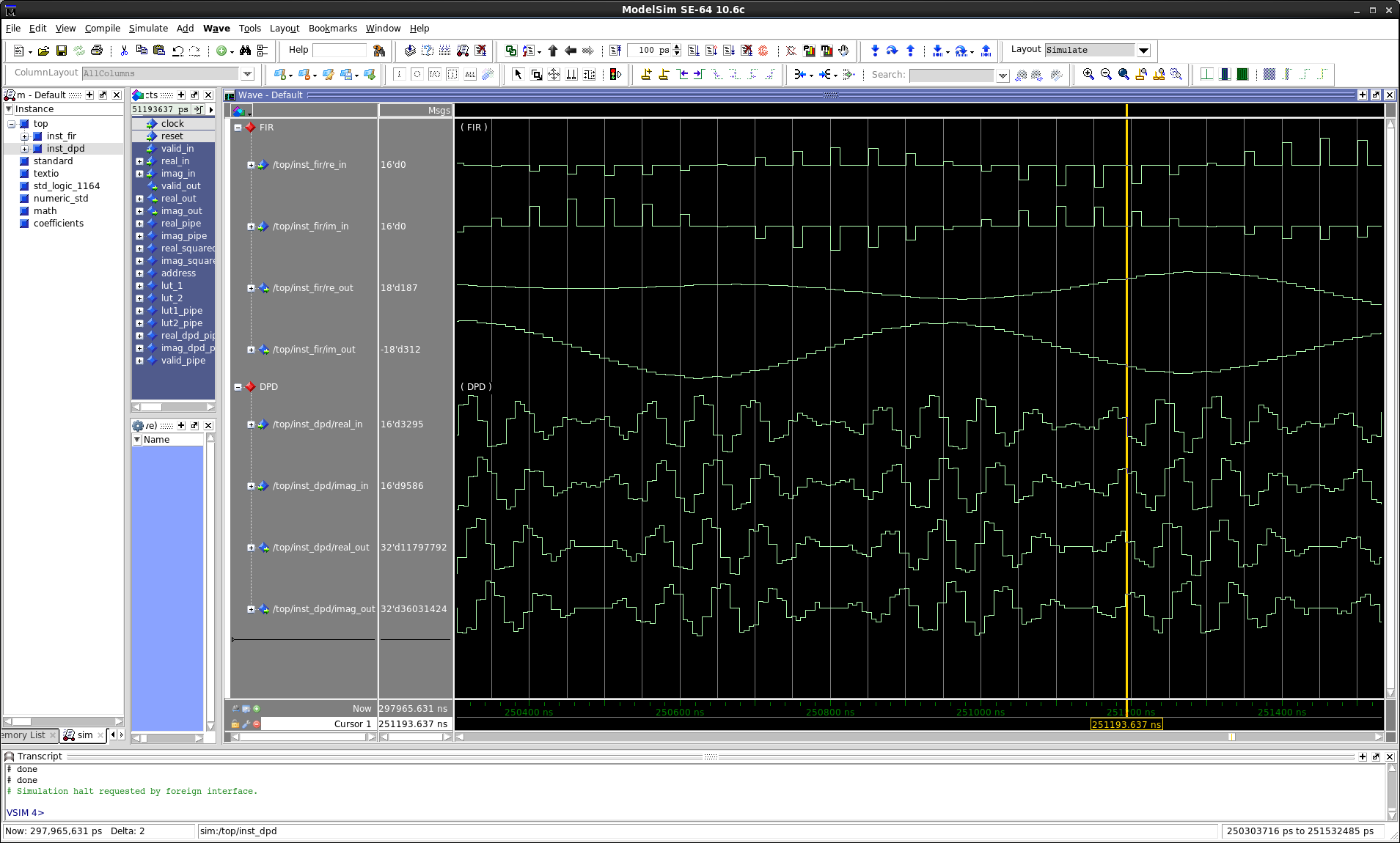
Simulink Simulations Results

Figure 58. Simulation

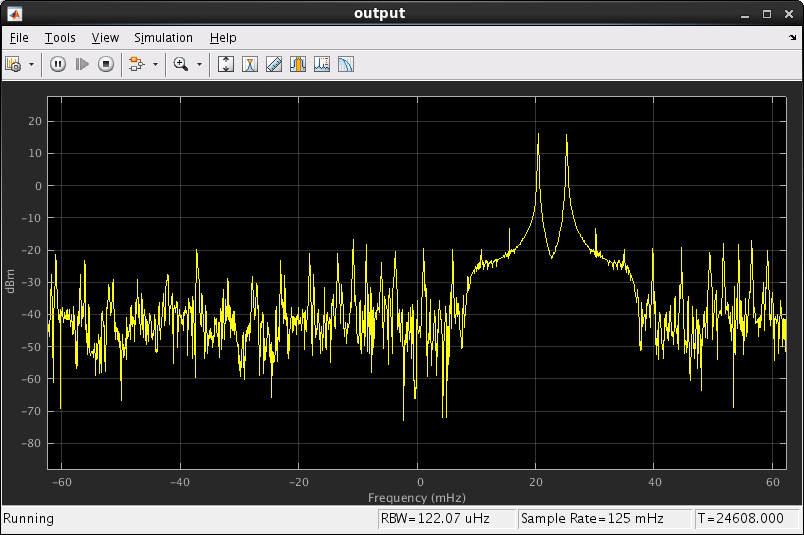
The first four waveforms are the real and imaginary input and output of the the FIR. The FIR smooths the zero-padded signals.

The next four waveforms are the real and imaginary input and output of the the DPD.

Figure 59. Upconverted

The two preloaded memory signals are clearly visible about 0, as are their four aliases because of the zero-insert upsampling.

Figure 60. Filtered

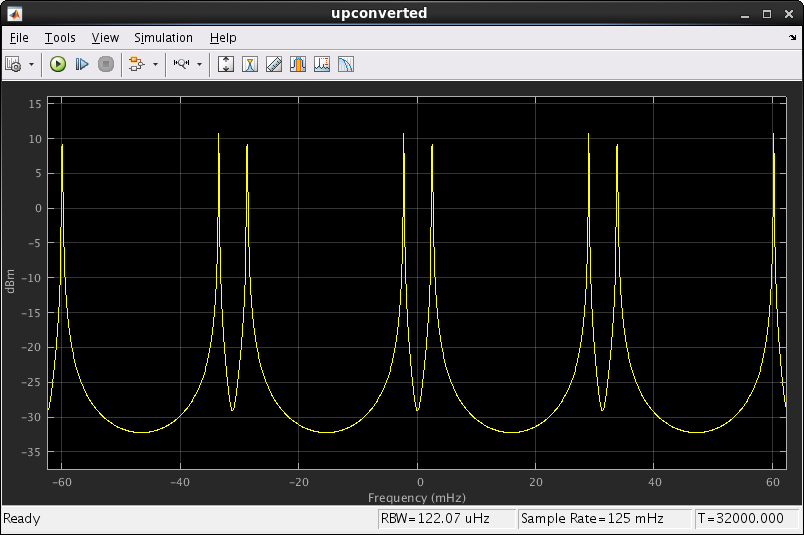
The aliased signals are attenuated by 40dB, as expected from the analysis in calc_fir_coefs.m.

Figure 61. Mixed

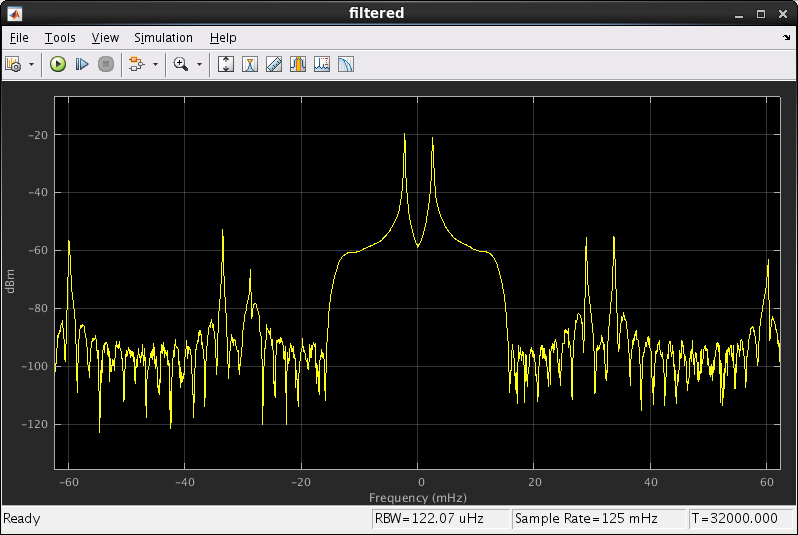
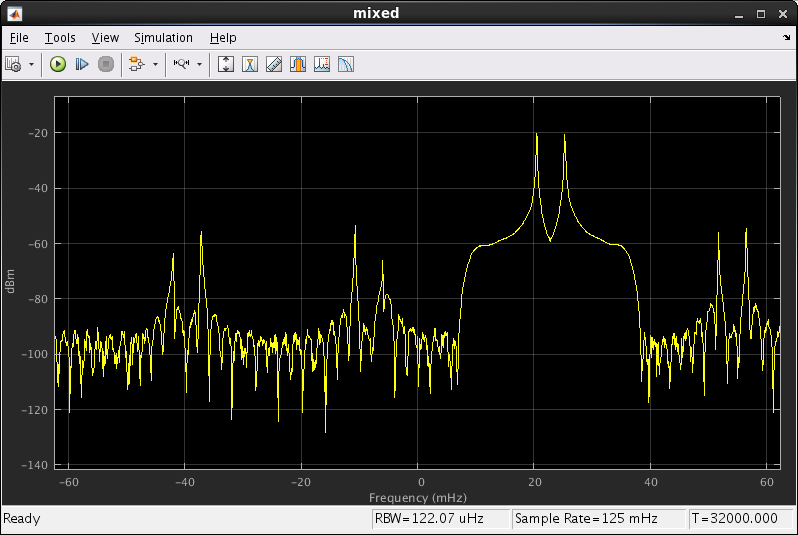
The mixed spectrum shows the baseband signal moving over to be centered on 16 MHz. This view shows the Simulink clock rate of 1 Hz rather than the FPGA clock rate of 640 MHz, so 16 MHz becomes 25 mHz.

Figure 62. Scaled

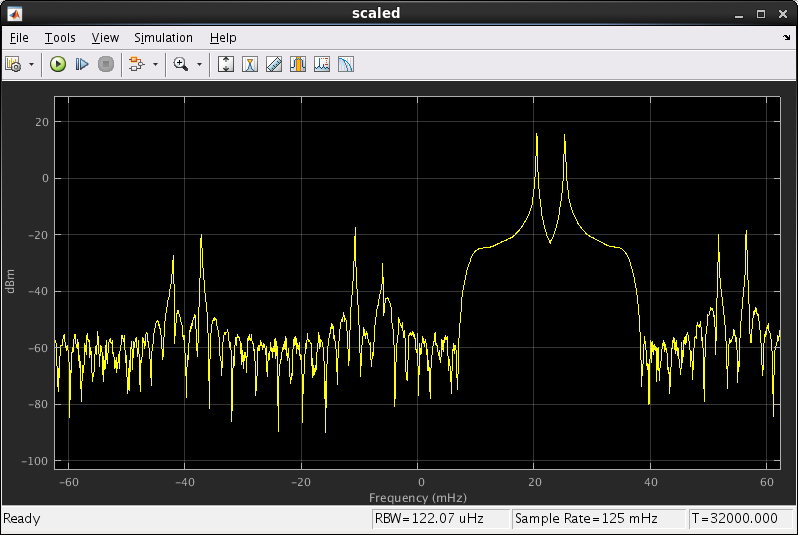
Scaled looks identical to mixed, except that the signal amplitude is much greater.

Figure 63. Output

The post-DPD output signal is a noiser version of the scaled signal. Observe the two third-order harmonics in the pass-band.

Related Information
Level Two Title