DSP Builder for Intel® FPGAs (Advanced Blockset): Handbook

Download PDF
ID 683337
Date 12/04/2023
Public

A newer version of this document is available. Customers should click here to go to the newest version.

Document Table of Contents
Document Table of Contents x
Answers to Top FAQs 1. About DSP Builder for Intel® FPGAs 2. DSP Builder for Intel FPGAs Advanced Blockset Getting Started 3. DSP Builder Design Flow 4. Primitive Library Blocks Tutorial 5. IP Tutorial 6. DSP Builder for Intel FPGAs (Advanced Blockset) Design Examples and Reference Designs 7. DSP Builder Design Rules, Design Recommendations, and Troubleshooting 8. About DSP Builder for Intel FPGAs Optimization 9. About Folding 10. Floating-Point Data Types 11. Design Configuration Library 12. IP Library 13. Interfaces Library 14. Primitives Library 15. Utilities Library 16. Simulink Supported Blocks 17. Document Revision History for DSP Builder for Intel FPGAs (Advanced Blockset) Handbook
1. About DSP Builder for Intel® FPGAs x
1.1. DSP Builder for Intel® FPGAs Features 1.2. DSP Builder for Intel® FPGAs Design Structure 1.3. DSP Builder for Intel® FPGAs Libraries 1.4. DSP Builder for Intel® FPGAs Device Support 1.5. FPGA Architecture Features for DSP Designs 1.6. DSP Design Flow in FPGAs 1.7. Software and Hardware DSP Design Flows in FPGAs
2. DSP Builder for Intel FPGAs Advanced Blockset Getting Started x
2.1. Installing DSP Builder for Intel® FPGAs 2.2. Licensing DSP Builder for Intel® FPGAs 2.3. Starting DSP Builder in MATLAB on Windows 2.4. Starting DSP Builder in MATLAB on Linux 2.5. Browsing DSP Builder Libraries and Adding Blocks to a New Model 2.6. Browsing and Opening DSP Builder Design Examples 2.7. Creating a New DSP Builder Design with the DSP Builder New Model Wizard 2.8. Simulating, Verifying, Generating, and Compiling Your DSP Builder Design
2.7. Creating a New DSP Builder Design with the DSP Builder New Model Wizard x
2.7.1. DSP Builder Menu Options 2.7.2. DSP Builder New Model Wizard Setup Script Parameters
3. DSP Builder Design Flow x
3.1. Implementing your Design in DSP Builder Advanced Blockset 3.2. Verifying your DSP Builder Advanced Blockset Design in Simulink and MATLAB 3.3. Exploring DSP Builder Advanced Blockset Design Tradeoffs 3.4. Verifying your DSP Builder Design with C++ Software Models 3.5. Verifying your DSP Builder Advanced Blockset Design in the ModelSim Simulator 3.6. Verifying Your DSP Builder Design in Hardware 3.7. Integrating Your DSP Builder Advanced Blockset Design into Hardware
3.1. Implementing your Design in DSP Builder Advanced Blockset x
3.1.1. Dividing your DSP Builder Design into Subsystems 3.1.2. Connecting DSP Builder Subsystems 3.1.3. Creating a New Design by Copying a DSP Builder Design Example 3.1.4. Vectorized Inputs
3.1.2. Connecting DSP Builder Subsystems x
3.1.2.1. DSP Builder Block Interface Signals 3.1.2.2. Periods 3.1.2.3. Sample Rate 3.1.2.4. Building Multichannel Systems 3.1.2.5. Channelization for Two Channels with a Folding Factor of 3 3.1.2.6. Channelization for Four Channels with a Folding Factor of 3 3.1.2.7. Synchronization and Scheduling of Data with the Channel Signal 3.1.2.8. Simulink vs Hardware Design Representations
3.1.2.1. DSP Builder Block Interface Signals x
3.1.2.1.1. Multichannel Systems with IP Library Blocks 3.1.2.1.2. Valid, Channel, and Data Examples
3.1.2.4. Building Multichannel Systems x
3.1.2.4.1. Multichannel Systems with IP Library Blocks
3.1.3. Creating a New Design by Copying a DSP Builder Design Example x
3.1.3.1. Creating a New Design From the DSP Builder FIR Design Example and Changing the Namespaces
3.2. Verifying your DSP Builder Advanced Blockset Design in Simulink and MATLAB x
3.2.1. Verifying your DSP Builder Advanced Blockset Design with a Testbench 3.2.2. Running DSP Builder Advanced Blockset Automatic Testbenches 3.2.3. Using DSP Builder Advanced Blockset References 3.2.4. Setting Up Stimulus in DSP Builder Advanced Blockset 3.2.5. Analyzing your DSP Builder Advanced Blockset Design
3.2.1. Verifying your DSP Builder Advanced Blockset Design with a Testbench x
3.2.1.1. Visualization Features
3.2.2. Running DSP Builder Advanced Blockset Automatic Testbenches x
3.2.2.1. dspba.runModelsimATB 3.2.2.2. Running All Automatic Testbenches 3.2.2.3. The command run_all_atbs Command Syntax 3.2.2.4. Testbench Error Messages
3.3. Exploring DSP Builder Advanced Blockset Design Tradeoffs x
3.3.1. Bit Growth 3.3.2. Managing Bit Growth in DSP Builder Advanced Blockset Designs 3.3.3. Using Rounding and Saturation in DSP Builder Advanced Blockset Designs 3.3.4. Scaling with Primitive Blocks 3.3.5. Changing Data Type with Convert Blocks and Specifying Output Types
3.3.5. Changing Data Type with Convert Blocks and Specifying Output Types x
3.3.5.1. The Convert Block and Real-world Values 3.3.5.2. Output Data Types on Primitive Blocks
3.4. Verifying your DSP Builder Design with C++ Software Models x
3.4.1. Software Model Options 3.4.2. Software Model Generated Files 3.4.3. Software Model Compilers 3.4.4. Compiling and Running Software Model Testbenches 3.4.5. Testing the Software Model 3.4.6. MATLAB MEX Function Wrapper for a Generated Software Model
3.4.5. Testing the Software Model x
3.4.5.1. Linking to External Libraries
3.4.6. MATLAB MEX Function Wrapper for a Generated Software Model x
3.4.6.1. Driving the Model 3.4.6.2. MEX Model Code 3.4.6.3. Complete the MEX Function 3.4.6.4. Compile, Run, and Test the MEX Function
3.5. Verifying your DSP Builder Advanced Blockset Design in the ModelSim Simulator x
3.5.1. Automatic Testbench 3.5.2. DSP Builder Advanced Blockset ModelSim Simulations
3.5.1. Automatic Testbench x
3.5.1.1. DSP Builder Advanced Blockset Automatic Testbench Files
3.6. Verifying Your DSP Builder Design in Hardware x
3.6.1. Hardware Verification
3.6.1. Hardware Verification x
3.6.1.1. Batch Hardware Verification Design Example 3.6.1.2. Real-Time Hardware Verification Design Example
3.7. Integrating Your DSP Builder Advanced Blockset Design into Hardware x
3.7.1. DSP Builder Generated Files 3.7.2. DSP Builder Designs and the Quartus Prime Project 3.7.3. Interfaces with a Processor Bus 3.7.4. DSP Builder Designs in Platform Designer
3.7.2. DSP Builder Designs and the Quartus Prime Project x
3.7.2.1. Adding a DSP Builder Advanced Blockset Design to an Existing Quartus Prime Project
3.7.3. Interfaces with a Processor Bus x
3.7.3.1. Assigning Base Addresses in DSP Builder Designs 3.7.3.2. Updating Registers with the Nios II Processor
3.7.4. DSP Builder Designs in Platform Designer x
3.7.4.1. Integrating a DSP Builder Design to a Platform Designer System 3.7.4.2. Modifying Avalon Streaming Blocks 3.7.4.3. Restrictions for DSP Builder Designs with Avalon Streaming Interface and AXI4-Stream Blocks 3.7.4.4. Connecting Conduit Interfaces
4. Primitive Library Blocks Tutorial x
4.1. Creating a Fibonacci Design from the DSP Builder Primitive Library 4.2. Setting the Parameters on the Testbench Source Blocks 4.3. Simulating the Fibonacci Design in Simulink 4.4. Modifying the DSP Builder Fibonacci Design to Generate Vector Signals 4.5. Simulating the RTL of the Fibonacci Design
5. IP Tutorial x
5.1. Creating an IP Design 5.2. Simulating the IP Design in Simulink 5.3. Viewing Timing Closure and Viewing Resource Utilization for the DSP Builder IP Design 5.4. Reparameterizing the DSP Builder FIR Filter to Double the Number of Channels 5.5. Doubling the Target Clock Rate for a DSP Builder IP Design
6. DSP Builder for Intel FPGAs (Advanced Blockset) Design Examples and Reference Designs x
6.1. DSP Builder Design Configuration Block Design Examples 6.2. DSP Builder FFT Design Examples 6.3. DSP Builder DDC Design Example 6.4. DSP Builder Filter Design Examples 6.5. DSP Builder Finite State Machine Design Example 6.6. DSP Builder Folding Design Examples 6.7. DSP Builder Floating Point Design Examples 6.8. DSP Builder Flow Control Design Examples 6.9. DSP Builder HDL Import Design Example 6.10. DSP Builder Host Interface Design Examples 6.11. DSP Builder Fixed-Point Matrix Multiply Engine Design Example 6.12. DSP Builder Platform Design Examples 6.13. DSP Builder Primitive Block Design Examples 6.14. DSP Builder Reference Designs 6.15. DSP Builder Waveform Synthesis Design Examples
6.1. DSP Builder Design Configuration Block Design Examples x
6.1.1. Scale 6.1.2. Local Threshold
6.2. DSP Builder FFT Design Examples x
6.2.1. FFT 6.2.2. FFT without BitReverseCoreC Block 6.2.3. IFFT 6.2.4. IFFT without BitReverseCoreC Block 6.2.5. Floating-Point FFT 6.2.6. Floating-Point FFT without BitReverseCoreC Block 6.2.7. Floating-Point iFFT 6.2.8. Floating-Point iFFT without BitReverseCoreC Block 6.2.9. Multichannel FFT 6.2.10. Multiwire Transpose 6.2.11. Parallel FFT 6.2.12. Parallel Floating-Point FFT 6.2.13. Single-Wire Transpose 6.2.14. Switchable FFT/iFFT 6.2.15. Variable-Size Fixed-Point FFT 6.2.16. Variable-Size Fixed-Point FFT without BitReverseCoreC Block 6.2.17. Variable-Size Fixed-Point iFFT 6.2.18. Variable-Size Fixed-Point iFFT without BitReverseCoreC Block 6.2.19. Variable-Size Floating-Point FFT 6.2.20. Variable-Size Floating-Point FFT without BitReverseCoreC Block 6.2.21. Variable-Size Floating-Point iFFT 6.2.22. Variable-Size Floating-Point iFFT without BitReverseCoreC Block 6.2.23. Variable-Size Low-Resource FFT 6.2.24. Variable-Size Low-Resource Real-Time FFT 6.2.25. Variable-Size Supersampled FFT 6.2.26. Variable-Size Supersampled FFT with Bit-Reverse
6.3. DSP Builder DDC Design Example x
6.3.1. DDC Design Example Subsystem 6.3.2. Building the DDC Design Example
6.3.2. Building the DDC Design Example x
6.3.2.1. DDC Design Example Generated Files
6.4. DSP Builder Filter Design Examples x
6.4.1. Complex FIR Filter 6.4.2. Decimating CIC Filter 6.4.3. Decimating FIR Filter 6.4.4. Filter Chain with Forward Flow Control 6.4.5. FIR Filter with Exposed Bus 6.4.6. Fractional FIR Filter Chain 6.4.7. Fractional-Rate FIR Filter 6.4.8. Half-Band FIR Filter 6.4.9. IIR: Full-rate Fixed-point 6.4.10. IIR: Full-rate Floating-point 6.4.11. Interpolating CIC Filter 6.4.12. Interpolating FIR Filter 6.4.13. Interpolating FIR Filter with Multiple Coefficient Banks 6.4.14. Interpolating FIR Filter with Updating Coefficient Banks 6.4.15. Root-Raised Cosine FIR Filter 6.4.16. Single-Rate FIR Filter 6.4.17. Super-Sample Decimating FIR Filter 6.4.18. Super-Sample Fractional FIR Filter 6.4.19. Super-Sample Interpolating FIR Filter 6.4.20. Variable-Rate CIC Filter
6.6. DSP Builder Folding Design Examples x
6.6.1. Position, Speed, and Current Control for AC Motors 6.6.2. Position, Speed, and Current Control for AC Motors (with ALU Folding) 6.6.3. About FOC 6.6.4. Folded FIR Filter
6.7. DSP Builder Floating Point Design Examples x
6.7.1. Black-Scholes Floating Point 6.7.2. Double-Precision Real Floating-Point Matrix Multiply 6.7.3. Fine Doppler Estimator 6.7.4. Floating-Point Mandlebrot Set 6.7.5. General Real Matrix Multiply One Cycle Per Output 6.7.6. Newton Root Finding Tutorial Step 1—Iteration 6.7.7. Newton Root Finding Tutorial Step 2—Convergence 6.7.8. Newton Root Finding Tutorial Step 3—Valid 6.7.9. Newton Root Finding Tutorial Step 4—Control 6.7.10. Newton Root Finding Tutorial Step 5—Final 6.7.11. Normalizer 6.7.12. Single-Precision Complex Floating-Point Matrix Multiply 6.7.13. Single-Precision Real Floating-Point Matrix Multiply 6.7.14. Simple Nonadaptive 2D Beamformer
6.8. DSP Builder Flow Control Design Examples x
6.8.1. Avalon-ST Interface (Input and Output FIFO Buffer) with Backpressure 6.8.2. Avalon-ST Interface (Output FIFO Buffer) with Backpressure 6.8.3. Kronecker Tensor Product 6.8.4. Parallel Loops 6.8.5. Primitive FIR with Back Pressure 6.8.6. Primitive FIR with Forward Pressure 6.8.7. Primitive Systolic FIR with Forward Flow Control 6.8.8. Rectangular Nested Loop 6.8.9. Sequential Loops 6.8.10. Triangular Nested Loop
6.9. DSP Builder HDL Import Design Example x
6.9.1. Performing a Cosimulation
6.10. DSP Builder Host Interface Design Examples x
6.10.1. Memory-Mapped Registers
6.12. DSP Builder Platform Design Examples x
6.12.1. 16-Channel DDC 6.12.2. 16-Channel DUC 6.12.3. 2-Antenna DUC for WiMAX 6.12.4. 2-Channel DUC 6.12.5. Super-Sample Rate Digital Upconverter
6.13. DSP Builder Primitive Block Design Examples x
6.13.1. 8×8 Inverse Discrete Cosine Transform 6.13.2. Automatic Gain Control 6.13.3. Bit Combine for Boolean Vectors 6.13.4. Bit Extract for Boolean Vectors 6.13.5. Color Space Converter 6.13.6. CORDIC from Primitive Blocks 6.13.7. Digital Predistortion Forward Path 6.13.8. Fibonacci Series 6.13.9. Folded Vector Sort 6.13.10. Fractional Square Root Using CORDIC 6.13.11. Fixed-point Maths Functions 6.13.12. Gaussian Random Number Generator 6.13.13. Hello World 6.13.14. Hybrid Direct Form and Transpose Form FIR Filter 6.13.15. Loadable Counter 6.13.16. Matrix Initialization of LUT 6.13.17. Matrix Initialization of Vector Memories 6.13.18. Multichannel IIR Filter 6.13.19. Quadrature Amplitude Modulation 6.13.20. Reinterpret Cast for Bit Packing and Unpacking 6.13.21. Run-time Configurable Decimating and Interpolating Half-Rate FIR Filter 6.13.22. Square Root Using CORDIC 6.13.23. Test CORDIC Functions with the CORDIC Block 6.13.24. Uniform Random Number Generator 6.13.25. Vector Sort—Sequential 6.13.26. Vector Sort—Iterative 6.13.27. Vector Initialization of Sample Delay 6.13.28. Wide Single-Channel Accumulators
6.14. DSP Builder Reference Designs x
6.14.1. 1-Antenna WiMAX DDC 6.14.2. 2-Antenna WiMAX DDC 6.14.3. 1-Antenna WiMAX DUC 6.14.4. 2-Antenna WiMAX DUC 6.14.5. 4-Carrier, 2-Antenna W-CDMA DDC 6.14.6. 1-Carrier, 2-Antenna W-CDMA DDC 6.14.7. 4-Carrier, 2-Antenna W-CDMA DUC 6.14.8. 4-Carrier, 4-Antenna DUC and DDC for LTE 6.14.9. 1-Carrier, 2-Antenna W-CDMA DDC 6.14.10. 4-Carrier, 2-Antenna High-Speed W-CDMA DUC at 368.64 MHz with Total Rate Change 32 6.14.11. 4-Carrier, 2-Antenna High-Speed W-CDMA DUC at 368.64 MHz with Total Rate Change 48 6.14.12. 4-Carrier, 2-Antenna High-Speed W-CDMA DUC at 307.2 MHz with Total Rate Change 40 6.14.13. Cholesky-based Matrix Inversion Parameters Performance and Resource Usage 6.14.14. Cholesky Solver Multiple Channels 6.14.15. Crest Factor Reduction 6.14.16. Direct RF with Synthesizable Testbench 6.14.17. Dynamic Decimating FIR Filter 6.14.18. Multichannel QR Decompostion 6.14.19. QR Decompostion 6.14.20. QRD Solver 6.14.21. Reconfigurable Decimation Filter 6.14.22. Single-Channel 10-MHz LTE Transmitter 6.14.23. STAP Radar Forward and Backward Substitution 6.14.24. STAP Radar Steering Generation 6.14.25. STAP Radar QR Decomposition 192x204 6.14.26. Time Delay Beamformer 6.14.27. Transmit and Receive Modem 6.14.28. Variable Integer Rate Decimation Filter
6.15. DSP Builder Waveform Synthesis Design Examples x
6.15.1. Complex Mixer 6.15.2. Four Channel, Two Banks NCO 6.15.3. Four Channel, Four Banks NCO 6.15.4. Four Channel, Eight Banks, Two Wires NCO 6.15.5. Four Channel, 16 Banks NCO 6.15.6. IP 6.15.7. NCO 6.15.8. NCO with Exposed Bus 6.15.9. Real Mixer 6.15.10. Super-sample NCO
7. DSP Builder Design Rules, Design Recommendations, and Troubleshooting x
7.1. DSP Builder Design Rules and Recommendations 7.2. Troubleshooting DSP Builder Designs
7.2. Troubleshooting DSP Builder Designs x
7.2.1. About Loops 7.2.2. Closing Timed feedback Loops 7.2.3. Loops, Clock Cycles, and Data Cycles
8. About DSP Builder for Intel FPGAs Optimization x
8.1. Associating DSP Builder with MATLAB 8.2. Setting Up Simulink for DSP Builder Designs 8.3. The DSP Builder Windows Shortcut 8.4. Setting DSP Builder Design Parameters with MATLAB Scripts 8.5. Managing your Designs 8.6. How to Manage Latency 8.7. Flow Control in DSP Builder Designs 8.8. Reset Minimization 8.9. About Importing HDL
8.2. Setting Up Simulink for DSP Builder Designs x
8.2.1. Setting Up Simulink Solver 8.2.2. Setting Up Simulink Signal Display Option
8.4. Setting DSP Builder Design Parameters with MATLAB Scripts x
8.4.1. Running Setup Scripts Automatically 8.4.2. Defining Unique DSP Builder Design Parameters 8.4.3. Example DSP Builder Custom Scripts
8.5. Managing your Designs x
8.5.1. Managing Basic Parameters 8.5.2. Creating User Libraries and Converting a Primitive Subsystem into a Custom Block 8.5.3. Revision Control
8.6. How to Manage Latency x
8.6.1. Reading the Added Latency Value for an IP Block 8.6.2. Zero Latency Example 8.6.3. Implicit Delays in DSP Builder Designs 8.6.4. Distributed Delays in DSP Builder Designs 8.6.5. Latency and fMAX Constraint Conflicts in DSP Builder Designs 8.6.6. Control Units Delays
9. About Folding x
9.1. ALU Folding 9.2. Removing Resource Sharing Folding
9.1. ALU Folding x
9.1.1. ALU Folding Limitations 9.1.2. ALU Folding Parameters 9.1.3. ALU Folding Simulation Rate 9.1.4. Using ALU Folding 9.1.5. Using Automated Verification 9.1.6. Ready Signal 9.1.7. Connecting the ALU Folding Ready Signal 9.1.8. About the ALU Folding Start of Packet Signal
10. Floating-Point Data Types x
10.1. DSP Builder Floating-Point Data Type Features 10.2. DSP Builder Supported Floating-Point Data Types 10.3. DSP Builder Round-Off Errors 10.4. Trading Off Logic Utilization and Accuracy in DSP Builder Designs 10.5. Upgrading Pre v14.0 Designs 10.6. Floating-Point Sine Wave Generator Tutorial 10.7. Newton-Raphson Root Finding Tutorial 10.8. Forcing Soft Floating-point Data Types with the Advanced Options
10.6. Floating-Point Sine Wave Generator Tutorial x
10.6.1. Creating a Sine Wave Generator in DSP Builder 10.6.2. Using Data Type Variables to Parameterize Designs 10.6.3. Using Data-Type Propagation in DSP Builder Designs 10.6.4. DSP Builder Testbench Verification
10.6.4. DSP Builder Testbench Verification x
10.6.4.1. Tuning ATB Thresholds 10.6.4.2. Writing Application Specific Verification 10.6.4.3. Bit-Accurate Simulation 10.6.4.4. Adder Trees and Scalar Products 10.6.4.5. Creating Floating-Point Accumulators for Designs that Use Iteration
10.7. Newton-Raphson Root Finding Tutorial x
10.7.1. Implementing the Newton Design 10.7.2. Improving DSP Builder Floating-Point Designs
11. Design Configuration Library x
11.1. Avalon Memory-Mapped Agent Settings (AvalonMemoryMappedAgentSettings) 11.2. Control 11.3. Device 11.4. LocalThreshold
11.2. Control x
11.2.1. DSP Builder Memory and Multiplier Trade-Off Options
12. IP Library x
12.1. Channel Filter and Waveform Library 12.2. Dependent Delay Library 12.3. FFT IP Library
12.1. Channel Filter and Waveform Library x
12.1.1. DSP Builder FIR and CIC Filters 12.1.2. DSP Builder FIR Filters 12.1.3. Channel Viewer (ChanView) 12.1.4. Complex Mixer (ComplexMixer) 12.1.5. Decimating CIC 12.1.6. Decimating FIR 12.1.7. Fractional Rate FIR 12.1.8. Interpolating CIC 12.1.9. Interpolating FIR 12.1.10. NCO 12.1.11. Real Mixer (Mixer) 12.1.12. Scale 12.1.13. Single-Rate FIR
12.1.1. DSP Builder FIR and CIC Filters x
12.1.1.1. Common CIC and FIR Filter Features 12.1.1.2. Updated Help 12.1.1.3. Half-Band and L-Band Nyquist FIR Filters 12.1.1.4. Parameterization of CIC and FIR Filters 12.1.1.5. Setting and Changing FIR Filter Coefficients at Runtime in DSP Builder
12.1.2. DSP Builder FIR Filters x
12.1.2.1. FIR Filter Avalon-MM Interfaces 12.1.2.2. Reconfigurable FIR Filters 12.1.2.3. FIR Filter Coefficient Sharing 12.1.2.4. FIR Filter Reset
12.1.10. NCO x
12.1.10.1. NCO Block Phase Increment and Inversion 12.1.10.2. NCO Block Phase Increment Memory Registers 12.1.10.3. NCO Block Frequency Hopping
12.2. Dependent Delay Library x
12.2.1. Dependent Latency Expressions
12.3. FFT IP Library x
12.3.1. Bit Reverse Core C (BitReverseCoreC and VariableBitReverse) 12.3.2. FFT (FFT, FFT_Light, VFFT, VFFT_Light)
13. Interfaces Library x
13.1. Memory-Mapped Library 13.2. Streaming Library
13.1. Memory-Mapped Library x
13.1.1. Bus Slave (BusSlave) 13.1.2. Bus Stimulus (BusStimulus) 13.1.3. Bus Stimulus File Reader (Bus StimulusFileReader) 13.1.4. External Memory, Memory Read, Memory Write 13.1.5. Register Bit (RegBit) 13.1.6. Register Field (RegField) 13.1.7. Register Out (RegOut) 13.1.8. Shared Memory (SharedMem)
13.2. Streaming Library x
13.2.1. Avalon-ST Input (AStInput) 13.2.2. Avalon-ST Input FIFO Buffer (AStInputFIFO) 13.2.3. Avalon-ST Output (AStOutput) 13.2.4. AXI4-Stream Blocks (AXI4StreamReceiver and AXI4StreamTransmitter)
14. Primitives Library x
14.1. Vector and Complex Type Support 14.2. DFT Design Elements Library 14.3. FFT Design Elements Library 14.4. Primitive Basic Blocks Library 14.5. Primitive Configuration Library 14.6. Primitive Design Elements Library
14.1. Vector and Complex Type Support x
14.1.1. Vector Type Support 14.1.2. Complex Support
14.1.1. Vector Type Support x
14.1.1.1. Element by Element Mode 14.1.1.2. Mathematical Vector Mode 14.1.1.3. Interactions with Simulink
14.1.2. Complex Support x
14.1.2.1. Interactions with Simulink
14.2. DFT Design Elements Library x
14.2.1. DFT (DFT) 14.2.2. Reorder (ReorderBlock) 14.2.3. Reorder and Rescale (ReorderAndRescale)
14.3. FFT Design Elements Library x
14.3.1. About Pruning and Twiddle for FFT Blocks 14.3.2. Bit Vector Combine (BitVectorCombine) 14.3.3. Butterfly Unit (BFU) 14.3.4. Butterfly I C (BFIC) (Deprecated) 14.3.5. Butterfly II C (BFIIC) (Deprecated) 14.3.6. Choose Bits (ChooseBits) 14.3.7. Crossover Switch (XSwitch) 14.3.8. Dual Twiddle Memory (DualTwiddleMemoryC) 14.3.9. Edge Detect (EdgeDetect) 14.3.10. Floating-Point Twiddle Generator (TwiddleGenF) (Deprecated) 14.3.11. Fully-Parallel FFTs (FFT2P, FFT4P, FFT8P, FFT16P, FFT32P, and FFT64P) 14.3.12. Fully-Parallel FFTs with Flexible Ordering (FFT2X, FFT4X, FFT8X, FFT16X, FFT32X, and FFT64X) 14.3.13. General Multitwiddle and General Twiddle (GeneralMultiTwiddle, GeneralMultVTwiddle, GeneralTwiddle, GeneralVTwiddle) 14.3.14. Hybrid FFT (Hybrid_FFT, HybridVFFT, HybridVFFT_btb) 14.3.15. Multiwire Transpose (MultiwireTranspose) 14.3.16. Multiwire Variable Bit Reverse (MultiwireVariableBitReverse) 14.3.17. Parallel Pipelined FFT (PFFT_Pipe) 14.3.18. Pulse Divider (PulseDivider) 14.3.19. Pulse Multiplier (PulseMultiplier) 14.3.20. Single-Wire Transpose (Transpose) 14.3.21. Split Scalar (SplitScalar) 14.3.22. Streaming FFTs (FFT2, FFT4, VFFT2, and VFFT4) 14.3.23. Stretch Pulse (StretchPulse) 14.3.24. Twiddle Angle (TwiddleAngle) 14.3.25. Twiddle Generator (TwiddleGenC) Deprecated 14.3.26. Twiddle and Variable Twiddle (Twiddle and VTwiddle) 14.3.27. Twiddle ROM (TwiddleRom, TwiddleMultRom and TwiddleRomF (deprecated))
14.4. Primitive Basic Blocks Library x
14.4.1. Absolute Value (Abs) 14.4.2. Accumulator (Acc) 14.4.3. Add 14.4.4. Add SLoad (AddSLoad) 14.4.5. AddSub 14.4.6. AddSubFused 14.4.7. AND Gate (And) 14.4.8. Bit Combine (BitCombine) 14.4.9. Bit Extract (BitExtract) 14.4.10. Bit Reverse (BitReverse) 14.4.11. Compare (CmpCtrl) 14.4.12. Complex Conjugate (ComplexConjugate) 14.4.13. Compare Equality (CmpEQ) 14.4.14. Compare Greater Than (CmpGE) 14.4.15. Compare Less Than (CmpLT) 14.4.16. Compare Not Equal (CmpNE) 14.4.17. Constant (Const) 14.4.18. Constant Multiply (Const Mult) 14.4.19. Convert 14.4.20. CORDIC 14.4.21. Counter 14.4.22. Count Leading Zeros, Ones, or Sign Bits (CLZ) 14.4.23. Dual Memory (DualMem) 14.4.24. Demultiplexer (Demux) 14.4.25. Divide 14.4.26. Fanout 14.4.27. FIFO 14.4.28. Floating-point Classifier (FloatClass) 14.4.29. Floating-point Multiply Accumulate (MultAcc) 14.4.30. ForLoop 14.4.31. Load Exponent (LdExp) 14.4.32. Left Shift (LShift) 14.4.33. Loadable Counter (LoadableCounter) 14.4.34. Look-Up Table (Lut) 14.4.35. Loop 14.4.36. Math 14.4.37. Minimum and Maximum (MinMax) 14.4.38. MinMaxCtrl 14.4.39. Multiply (Mult) 14.4.40. Multiplexer (Mux) 14.4.41. NAND Gate (Nand) 14.4.42. Negate 14.4.43. NOR Gate (Nor) 14.4.44. NOT Gate (Not) 14.4.45. OR Gate (Or) 14.4.46. Polynomial 14.4.47. Ready 14.4.48. Reinterpret Cast (ReinterpretCast) 14.4.49. Round 14.4.50. Sample Delay (SampleDelay) 14.4.51. Scalar Product 14.4.52. Select 14.4.53. Sequence 14.4.54. Shift 14.4.55. Sqrt 14.4.56. Subtract (Sub) 14.4.57. Sum of Elements (SumOfElements) 14.4.58. Trig 14.4.59. XNOR Gate (Xnor) 14.4.60. XOR Gate (Xor)
14.5. Primitive Configuration Library x
14.5.1. Channel In (ChannelIn) 14.5.2. Channel Out (ChannelOut) 14.5.3. General Purpose Input (GPIn) 14.5.4. General Purpose Output (GPOut) 14.5.5. Synthesis Information (SynthesisInfo)
14.5.5. Synthesis Information (SynthesisInfo) x
14.5.5.1. Scheduled Synthesis 14.5.5.2. Updated Help
14.6. Primitive Design Elements Library x
14.6.1. Anchored Delay 14.6.2. Complex to Real-Imag 14.6.3. Enabled Delay Line 14.6.4. Enabled Feedback Delay 14.6.5. Expand Scalar (ExpandScalar) 14.6.6. Finite State Machine 14.6.7. Nested Loops (NestedLoop1, NestedLoop2, NestedLoop3) 14.6.8. Pause 14.6.9. Reset-Priority Latch (SRlatch_PS) 14.6.10. Same Data Type (SameDT) 14.6.11. Set-Priority Latch (SRlatch) 14.6.12. Single-Cycle Latency Latch (latch_1L) 14.6.13. Tapped Line Delay (TappedLineDelay) 14.6.14. Variable Super-Sample Delay (VariableDelay) 14.6.15. Vector Fanout (VectorFanout) 14.6.16. Vector Multiplexer (VectorMux) 14.6.17. Zero-Latency Latch (latch_0L)
14.6.6. Finite State Machine x
14.6.6.1. Adding a Finite State Machine Block to your DSP Builder Design 14.6.6.2. Modifying the Finite State Machine Block Specification File 14.6.6.3. Implement Token Passing with the Finite State Machine 14.6.6.4. Implementing a One Shot Counter with the Finite State Machine 14.6.6.5. Specifying ForLoop Control Units 14.6.6.6. Creating the Finite State Machine Configuration File 14.6.6.7. Upgrading Finite State Machine Blocks from v23.2 and Earlier
15. Utilities Library x
15.1. Analyze and Test Library 15.2. HDL Import Library 15.3. Beta Blocks Library
15.1. Analyze and Test Library x
15.1.1. Capture Values 15.1.2. Dechannelizer 15.1.3. Channelizer 15.1.4. Display Resources 15.1.5. Edit Params 15.1.6. Pause
15.2. HDL Import Library x
15.2.1. HDL Import 15.2.2. HDL Import Config
15.3. Beta Blocks Library x
15.3.1. SYCL
15.3.1. SYCL x
15.3.1.1. Implementing a SYCL Block
Answers to Top FAQs
1. About DSP Builder for Intel® FPGAs
2. DSP Builder for Intel FPGAs Advanced Blockset Getting Started
3. DSP Builder Design Flow
4. Primitive Library Blocks Tutorial
5. IP Tutorial
6. DSP Builder for Intel FPGAs (Advanced Blockset) Design Examples and Reference Designs
7. DSP Builder Design Rules, Design Recommendations, and Troubleshooting
8. About DSP Builder for Intel FPGAs Optimization
9. About Folding
10. Floating-Point Data Types
11. Design Configuration Library
12. IP Library
13. Interfaces Library
14. Primitives Library
15. Utilities Library
16. Simulink Supported Blocks
17. Document Revision History for DSP Builder for Intel FPGAs (Advanced Blockset) Handbook

6.14.13. Cholesky-based Matrix Inversion

Matrix inversion has many applications in wireless communications, e.g. digital predistortion (DPD) for RF linearization and multiple-input multiple-output (MIMO) detection. Matrix inversion algorithms typically require high-resolution numerics to guarantee accuracy and numerical stability. The implementation is normally resource demanding in particular if the matrix dimension grows. The DSP Builder Cholesky-based Matrix Inversion reference design offers an efficient implementation of matrix inversion for minimized resource utilization and improved latency and throughput. The Cholesky decomposition technique inverts a positive-definite real or complex square matrix. Cholesky decomposition-based matrix inversion is more efficient than direct matrix inversion.
Figure 83. Matrix inversion based on Cholesky decompositionThe figure shows the three steps of implementing a Hermitian matrix inversion using Cholesky decomposition:
  1. Cholesky decomposition
  2. Triangular matrix inversion through forward substitution
  3. Triangular matrix multiplication

The Cholesky decomposition calculates the reciprocal values of the diagonal elements of L, which the triangular matrix inversion requires. The design propagates those values to the output interface of the Cholesky decomposition reducing resource usage and latency.

Assuming matrix A is an NxN positive-definite square matrix, Cholesky decomposition of A into lower and upper triangular matrices, L, and L H is given by:

A = LH

The inverse of Hermitian A, A -1 is:

The design performs Cholesky decomposition and calculates the inverse of L, , through forward substitution. J is a lower triangle matrix. The inverse of the input matrix requires a triangular matrix multiplication, followed by a Hermitian matrix multiplication:

The Cholesky-based matrix inversion reference design comprises a Cholseky decomposition design and a triangular matrix inversion design. Both designs are fully pipelined, with multichannel input and output streaming to maximize throughput. The size of dot-product engines in both designs are compile-time configurable according to the size of the input matrices. The datapath and control logic are split.

Figure 84. Cholesky Decomposition Top-level DesignInput = size × (size +1) × channel/2
Figure 85. Triangular Matrix Inversion Top-level Design

This design supports single-precision floating-point Cholesky matrix inversion. DSP Builder requires a single-precision floating-point input for the floating point inversion.

Matrix inversion takes multiple matrices and interleaves the inverse computations for all matrices. This method hides the latency in computing each element by pipelining inversion of a completely different channel. Multichannel designs use the idle cycles in the computation chain to process the next channel. Two buffers at the input and output of the design create channels for streaming matrices into multichannel interfaces.

Table 19.  Top-level matrix inversion input and output portsThe input and output interfaces follow Avalon™ streaming standard.
Signal Direction Type Width Description
Sink_Valid Input Boolean 1 Avalon streaming sink valid signal for the input matrix interface. Number of valid input = (matrix size*(matrix size + 1))/2
Sink_Channel Input unsigned integer 8 Avalon streaming sink channel bus for the input matrix interface.
Sink_Data Input Single floating-point complex 64 bit I/Q Avalon streaming sink data bus for the input matrix interface. Lower matrix elements are streamed in column major order.
Source_Valid Output Boolean 1 Avalon streaming source valid signal for output interface. This signal is asserted for (size*(size+1))/2 clocks
Source_Channel Output unsigned integer 8 Avalon streaming source channel bus for output interface.
Source_Data Output Single floating-point complex 64 bit I/Q Avalon streaming source data bus for output interface. Lower matrix elements are streamed in column major order.

Parameters

Table 20.  Parameters of the matrix inversion designThe parameters are compile-time configurable using the setup file. .
Parameter Description
Size of Matrix The size of matrix to invert.
Channels Number of matrices inverted in a burst. Minimum of 16 channel.
Latency The period in cycles the module waits before receiving the next set of matrices.

DSP Builder calculates the throughput of the design by setting the latency value and the system clock:

Throughput (matrix inversion per second) = System clock/Latency

Although elements of input matrices arrive in streaming format, the internal channelizer vectorizes the input matrices into several channels (the default is 16). This vectorization significantly improves the throughput.

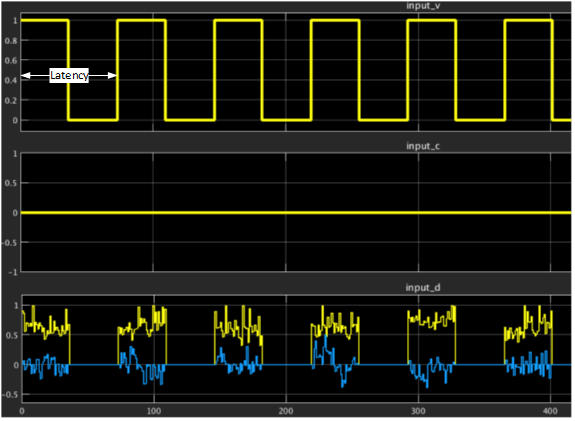
Figure 86. Input streaming interface for 8x8 Hermitian input matrix

The figure shows the latency configuration parameter in the input interface including data, valid, and channel signals. In this example of 8x8 matrix inversion, the valid signal remains high for 36 clock cycles (total number of lower triangle elements of the Hermitian matrix of 8x8) and remains low for (latency – 36) cycles before inserting the next matrix elements. The minimum duration to remain low and hence the minimum latency period may vary depending on the matrix size and the pipelining required to meet timing constraints.

Table 21.  Recommended Values for the Minimum Latency (maximum throughput) In Intel Stratix 10 and Intel Arria 10 devices, speed grade –1 and –2, for three different matrix sizes.
Matrix Dimension Latency in clock cycles
Intel Arria 10 Devices Intel Stratix 10 Devices
4x4 ≥ 30 ≥ 30
8x8 ≥ 75 ≥ 74
16x16 ≥ 230 ≥ 220

Performance and Resource Usage

Table 22.  Floating-point implementation resource utilization targeting Intel® Stratix® 10 GX/SX/TX 280 FPGAThe table shows the resource count of the floating-point Cholesky-based matrix inversion design including the channelizing input and output buffers.
Matrix Dimension Number of channels Logic Elements (ALMs) DSP Blocks Memory bits RAM blocks Registers
4x4 16 8,236 55 548,448 55 22,066
8x8 16 16,665 103 2,001,664 194 45,463
16x16 16 35,025 199 7,085,088 521 95,079
Table 23.  Performance of the floating-point matrix inversion module for different matrix dimensionsThis table shows the fMAX performance of the floating-point design for different matrix sizes with a system clock of 368.64 MHz and targeting a Intel® Stratix® 10 FPGA device. The maximum throughput is in millions of matrix inversions per second.
Matrix Dimension Number of channels Target System clock (MHz) fMAX (MHz) ThroughputMAX
4x4 16 368.64 468.06 12.2
8x8 16 368.64 403.88 5.0
16x16 16 368.64 392.77 1.67
Level Two Title