DSP Builder for Intel® FPGAs (Advanced Blockset): Handbook
A newer version of this document is available. Customers should click here to go to the newest version.
7.11. DSP Builder Fixed-Point Matrix Multiply Engine Design Example
Calculation: A(NxM) * B(MxL) = R(NxL)
The calculation is O(N) in time as the design unrolls two levels of inner loop in the matrix multiply. At the innermost level, the design unrolls the dot product as a systolic DSP chain or column. At the next level, the design unrolls and calculates L columns in parallel.
Essentially, matrix B appears in hardware as L DSP columns each of depth M. The calculation is O(ML) in area.
The calculation broadcasts each matrix A row in turn down all the L columns of this B layout in parallel.
This design takes input streams and produces an output stream. Ensure external components have the same input and output data format as the engine. Matrix A is a streamed input and has no block storage in the design but has pipelining. Matrix B is also a streamed input and storage is only of each element at the relevant node in the matrix grid in hardware.
The input streaming order for matrix A is M-in-parallel, with each of its N rows in turn. The input streaming order for matrix B (when M=N) is L-in-parallel, with each of its M rows in turn. You supply matrix A and B into the design simultaneously (under a single data valid flag). The output resultant matrix R is streamed L-in-parallel, with each of its N rows in turn. For more information about parallel inputs, calculations, and outputs, refer to Skew.
Matrix Multiply Engine Design Parameters
The design allows you to set the dimensions N, M, and L, real or complex matrix multiply data (cplx), and the input data width in bits (dw). You can also change the target device at the device block and the target frequency (fmax).
The design imposes a constraint on the relative values of N and M. The design rejects invalid values (refer to Engine Balance).
Ensure your design configuration is suitable for the target FPGA. For example, a large single matrix multiply engine is a complex matrix multiply of N=M=L=32 or real matrix multiply of N=M=L=48. A high frequency target for an engine is 600 MHz for an Intel Stratix 10 speed-grade 1 or 700 to 800 MHz for an Intel® Agilex™ 7 speed grade 1.
Setup and Check Scripts
The setup and check scripts, which configure the input and output, define the required interface to your configuration of the engine from a top-level design.
The engine comprises two main library components in sequence: data sequencer, dot product engine array.
The sequencer provides the data appropriately to the dot product engine that performs the calculation. The design places these library components in a testbench and checks engine behavior against reference MATLAB matrix multiplies. For more information, refer to the setup and check scripts.
Engine Balance
The design balances parallel input, calculation, and output rates to prevent bottlenecks. When you configure the engine it selects appropriate input, calculation, and output parallelism, to process one row per clock-cycle.
Where N=M=L, the dimensions are all equal. The design uses a single quantity for all aspects of the engine (one vector size for parallel: A input, B input, calculation, R output). The design has no constraint on the L value. L is independent of N and M values. The B input and R output is nominally L-in-parallel. The design has L DSP-columns in parallel. Where N, M have different values, the design achieves balance by delivering the input and output in N cycles. The design asserts the following constraint on a single engine:
- M must be a positive integer multiple of N: M = iN i.e. M = 1*N, 2*N, etc. When i>1, to balance rates, supply the B input as iL columns in parallel. The interleave and batching of these i*L inputs is:
- the first (i=0) L-parallel inputs, over N clock-cycles, feed the first N of M rows of B;
- the second (i=1) L-parallel inputs are delayed by N cycles and feed the second N of M rows; etc.
Generally, the design can process any values of N and M by combining the above constraint and k multiple engines. It finds k,I such that kM = iN.
Multiple engines work best when N and M share a large greatest common divisor (GCD). However, if for example N and M are relatively prime, you may pad one or other of them (refer to Pad).
For example, consider M ≠ iN with a reasonable GCD(M,N):
- M>N but M!=iN for any positive integer i. For i=1.5 (e.g. N=8, M=12), GCD=4: The design implements two engines configured as N=4, M=12 (M=3N). Each engine takes the top and bottom half of A and the same 3 row-slices of B.
- M<N For N=2*M (e.g. N=8, M=4, GCD=4), run two matrix multiply engines in parallel each with the same B input but distinct inputs of the upper and lower halves (rows) of A.
Alternatively, you can run a single engine twice with the same B input both times (or make new B input optional). The choice depends on your bandwidth requirements.
Pad
For some values of N and M, you can pad an engine dimension (N or M) so that they have a relationship compatible with larger designs.
When you pad a dimension, the design no longer fully uses all the input, calculation, and outputs. Effectively, the design pads the relevant input dimension by zero input. Consider a smaller primed dimension, e.g. N', as the real desired size versus the standard unprimed dimension, N, as the padded size.
When N'<N, the required design is essentially the same but it has some unused bandwidth for: A input rows, calculation, and R output rows (refer to Elastic N.)
When M'<M, you can optimize your design. The design has less A input columns per cycle (shrink input vector M to M'), a reduced dot-product calculation length (shrink M to M'). Also, the design has less B input rows, which you see as unused bandwidth rather than a physical design reduction.
Matrix Multiply Engine in Larger Designs
The engine design sequences top-level library components from library mm_lib.mdl. You can reuse this library in your own design. The engine design and scripts demonstrate configurations of a single engine. Explore and confirm configuration and validation before you implement the engine design.
When you implement the design, consider:
- Matching engine data throughput to that of your design
- Potentially dealing with N vs M constraint; adjusting manual skew
- Dealing with data skew (refer to Skew).
If your desired matrix multiply properties are not a simple fit to the single engine design, consider the following techniques: transpose form, blocking, multiple engines, pad.
Transpose Form
A * B = (BT * AT) T
The engine calculates BT * AT = RT. You can consider if the following transpose form is a better fit when adopting this engine:
Remap or reinterpret the transposed form to the standard parameters for the engine design.
Blocking
The design does not put bottlenecks on the input, calculation, and output.
A lower external bandwidth limit on input or output, artificially restricts the engine throughput. If the external I/O limits are close to engine throughput, you may choose to use them. If the I/O limits are lower than the engine, you can balance throughput and reduce resources by blocking the matrix multiply. With blocking the design chops the overall matrix into smaller blocks, feeds them through the engine in series and then sums them appropriately.
Consider blocking when the size of a singular matrix multiply is too large to fit the available FPGA resources.
Generally, you can configure an engine that is a fraction of the full desired matrix multiply and feed and combine blocks of such partial matrix multiplies to form the full matrix multiply.
If only N or L (but not M) are reduced, the resultant submatrices are independent, maximizing calculating ease and flexibility.
Elastic N
If you do not need to update matrix B on every matrix multiply, you can configure the engine with a nominal value of N that is not the real N. Alternatively, you can vary the real desired N at run time.
As matrix A streams row-after-row and if you do not update matrix B every time, you can interpret the data stream as sequentially multiplying A0*B and, A1*B, or a single multiplication of A01*B where A01 is the vertical concatenation of A0 and A1.
Skew
Skew applies to parallel processing of input, calculation, and output. The design can stagger the parallel vector successively across several clock-cycles rather than deliver them simultaneously. Skew is always a compile-time constant of a given design configuration. You cannot vary it at run time.
Skew is a mapping for each vector element to its delay. When this mapping is all zeroes, all elements in the vector are simultaneous. When skew is 0:(M-1), each element is successively delayed by one clock cycle (a skew rate of 1).
The minimal requirement of a skew mapping s() is that it doesn't decrease. For two vector indices i,j if i>=j, s(i)>=s(j). Typically, a skew mapping is based at zero s(0)=0. However, in some circumstances, you can also express a general pipelining delay p by adding it to all skew map elements.
The design processes the same vector width irrespective of the skew. Skew only affects the timing relationship between vector elements.
The design has systolic skew and scheduled skew.
Using the FPGA systolic DSP-column gives a skew rate of 1 and a skew mapping of 0:(M-1)), which is systolic skew. Systolic skew applies always on the matrix A input and is the only algorithmically imposed skew in the design.
As vector matrix sizes increase you may also deliberately apply scheduled skew to mitigate against the increased geographic dispersion of resources.
Scheduled skew may be zero (unnecessary) for small or low-frequency designs. As size and or frequency targets increase, the design might need scheduled skew to meet timing.
The design includes a base model for scheduled skew. Tune or replace this model to maximize your design efficiency.
The following diagram shows in summary all the possible effects (skews and M!=N) that may apply to an engine’s input A and B and output R, where time (and the matrix row input) flows down the page.
For input A, systolic skew (sharp downward slope) is always present.
For input B, you may apply a scheduled skew (subtle downward slope) to help to meet timing. For B if M=iN for integer i>1, provide B in i parallel stripes of rows delayed successively by N. The figure shows i=2.
For output R, the design repeats any scheduled skew you apply to the input B.
The matrix multiply operates on preceding and succeeding matrix multiplies for 100% resource usage and maximum throughput.
Basic Configurations
| N | M | L | Symbolic | Single Engine Solution |
|---|---|---|---|---|
| 1 | 1 | 1 | 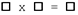 |
Yes |
| 1 | 1 | 2 |  |
Yes |
| 1 | 2 | 1 | 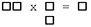 |
Yes |
| 1 | 2 | 2 |  |
Yes |
| 2 | 1 | 1 | 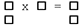 |
No. Use 2x base engine. Each receive same B but respectively top and bottom halves of A. Each produces top and bottom halves of R. 2x [N=1, M=1, L=1; 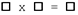 ] ] |
| 2 | 1 | 2 |  |
No. Use 2x base engine. Each receive same B but respectively top and bottom halves of A. Each produces top and bottom halves of R 2x [N=1, M=1, L=2;  ] ] |
| 2 | 2 | 1 |  |
Yes |