2.8.5. Loops in a Single Work-Item Kernel

Intel® FPGA SDK for OpenCL™ Standard Edition: Best Practices Guide

Download PDF

ID 683176

Date 9/24/2018

Version 18.1

Public

Visible to Intel only — GUID: pmi1517938463223

Ixiasoft

View Details

2.8.5. Loops in a Single Work-Item Kernel

The implements an algorithm that optimizes kernels to maximize performance for data processing.

The datapath of a loop within a single work-item kernel can contain multiple iterations in flight. This behavior is different from a loop within an NDRange kernel in that an NDRange kernel's loop contains multiple work-items in flight. An optimally unrolled loop is a loop iteration that is launched every clock cycle. Launching one loop iteration per clock cycle maximizes pipeline efficiency and yields the best performance. As shown in the figure below, launching one loop per clock cycle allows a kernel to finish faster.

Figure 49. Comparison of the Launch Frequency of a Loop Iteration Between a Non-Pipelined Loop and a Pipelined Loop

The launch frequency of a new loop iteration is called the initiation interval (II). II refers to the number of hardware clock cycles for which the pipeline must wait before it can process the next loop iteration. An optimally unrolled loop has an II value of 1 because one loop iteration is processed every clock cycle.

In the HTML report, the loop analysis of an optimally unrolled loop will state that the offline compiler has pipelined the loop successfully.

Consider the following example:

kernel void simple_loop (unsigned N,
                         global unsigned* restrict b, 
                         global unsigned* restrict c, 
                         global unsigned* restrict out)
{
    for (unsigned i = 1; i < N; i++) { 
        c[i] = c[i-1] + b[i];
    }
    out[0] = c[N-1];
}

Figure 50. Hardware Representation of the Kernel simple_loop

The figure depicts how the offline compiler leverages parallel execution and loop pipelining to execute simple_loop efficiently. The loop analysis report of this simple_loop kernel will show that for loop "for.body", the Pipelined column will indicate Yes, and the II column will indicate 1.

Trade-Off Between Critical Path and Maximum Frequency

The offline compiler attempts to achieve an II value of 1 for a given loop whenever possible. It some cases, the offline compiler might strive for an II of 1 at the expense of a reduced target f_max.

Consider the following example:

kernel void nd (global int *dst, int N) {
    int res = N;
    #pragma unroll  9
    for (int i = 0; i < N; i++) {
	    res += 1;
	    res ^= i;
    }
    dst[0] = res;
}

The following logical diagram is a simplified representation of the actual, more complex hardware implementation of kernel nd.

Figure 51. Logical Diagram for the Loop in Kernel nd

Figure 52. Actual Hardware Implementation of Kernel nd

The feedback with the addition operation and the XOR gate is the critical path that limits the offline compiler's ability to achieve the target frequency. The resulting HTML report describes a breakdown, in percentages, of the contributors that make up the critical path.

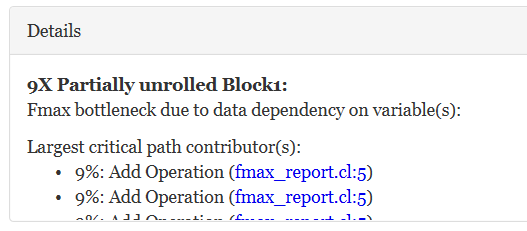
Figure 53. Details Pane of the Loop Analysis Report for Kernel ndThe line "9%: Add Operation (fmax_report.cl:5)" repeats nine times, one for each feedback.

Loop-Carried Dependencies that Affect the Initiation Interval of a Loop

There are cases where a loop is pipelined but it does not achieve an II value of 1. These cases are usually caused by data dependencies or memory dependencies within a loop.

Data dependency refers to a situation where a loop iteration uses variables that rely on the previous iteration. In this case, a loop can be pipelined, but its II value will be greater than 1. Consider the following example:

 1  // An example that shows data dependency
 2  // choose(n, k) = n! / (k! * (n-k)!)
 3
 4  kernel void choose( unsigned n, unsigned k, 
 5                      global unsigned* restrict result )
 6  {
 7      unsigned product = 1;
 8      unsigned j = 1;
 9
10      for( unsigned i = k; i <= n; i++ ) {
11          product *= i;
12          if( j <= n-k ) {
13              product /= j;
14          }
15          j++;
16      }
17
18      *result = product;
19  }

For every loop iteration, the value for the product variable in the kernel choose is calculated by multiplying the current value of index i by the value of product from the previous iteration. As a result, a new iteration of the loop cannot launch until the current iteration finishes processing. The figure below shows the logical view of the kernel choose, as it appears in the system viewer.

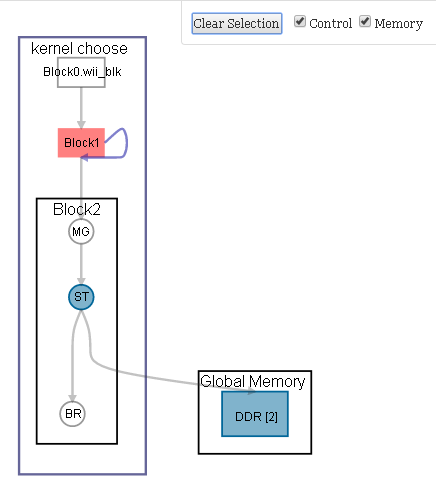
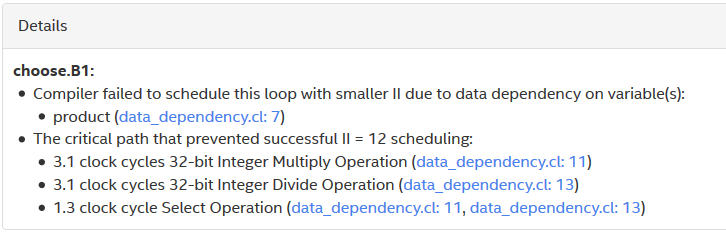
Figure 54. Logical View of the Kernel choose

The loop analysis report for the kernel choose indicates that Block1 has an II value of 13. In addition, the details pane reports that the high II value is caused by a data dependency on product, and the largest contributor to the critical path is the integer division operation on line 13.

Figure 55. Loop Analysis Report of the Kernel choose

Figure 56. Information in the Details Pane of the Loop Analysis Report for the Kernel choose

Memory dependency refers to a situation where memory access in a loop iteration cannot proceed until memory access from the previous loop iteration is completed. Consider the following example:


1  kernel void mirror_content( unsigned max_i,
2                              global int* restrict out)
3  {
4    for (int i = 1; i < max_i; i++) {
5      out[max_i*2-i] = out[i];
6    }
7  }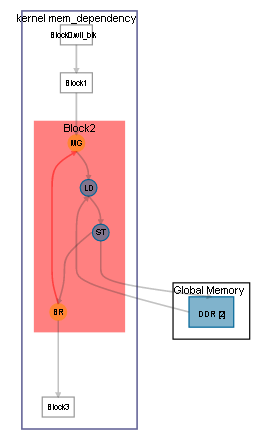

Figure 57. Logical View of the Kernel mirror_content

In the loop analysis for the kernel mirror_content, the details pane identifies the source of the memory dependency and the breakdown, in percentages, of the contributors to the critical path for Block2.

Figure 58. Details Pane of the Loop Analysis for the Kernel mirror_content

Select Your Language

Using Intel.com Search

Quick Links

Recent Searches

Advanced Search

Only search in

Intel® FPGA SDK for OpenCL™ Standard Edition: Best Practices Guide

2.8.5. Loops in a Single Work-Item Kernel

Trade-Off Between Critical Path and Maximum Frequency

Loop-Carried Dependencies that Affect the Initiation Interval of a Loop