Intel® FPGA SDK for OpenCL™ Standard Edition: Best Practices Guide
2.6. Optimizing an OpenCL Design Example Based on Information in the HTML Report
OpenCL design example that performs matrix square AxA:
// performs matrix square A*A
// A is a square len*len matrix
kernel void matrix_square (global float* restrict A,
unsigned len,
global float* restrict out) {
for(unsigned oi = 0; oi < len*len; oi++) {
float sum = 0;
int row = oi % len;
for (int col = 0; col < len; col++) {
unsigned i = (row * len) + col; // 0, 1, 2, 3, 4,...
unsigned j = (col * len) + row; // 0, 3, 6, 9, 1,...
sum += A[i] * A[j];
}
out[oi] = sum;
}
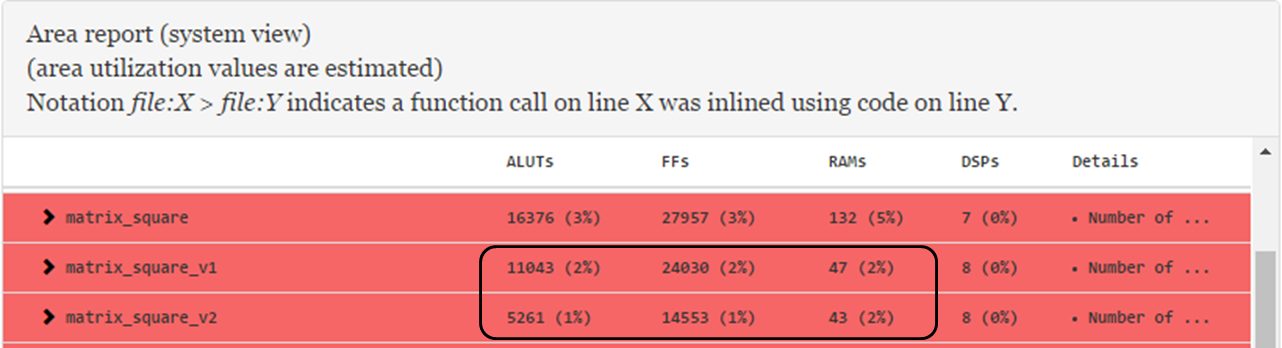
}The system view of the area report for the kernel matrix_square indicates that the estimated usages of flipflops (FF) and RAMs for Block3 are high. Further examination of Block3 in the system viewer shows that Block3 also has a high latency value.

The cause for these performance bottlenecks is because the system is loading data from global memory from inside a loop. Therefore, the first optimization step you can take is to preload the data into local memory, as shown in the modified code below.
kernel void matrix_square_v1 (global float* restrict A,
unsigned len,
global float* restrict out)
{
// 1. preload the data into local memory
// - suppose we know the max size is 4X4
local int cache_a[16];
for(unsigned k = 0; k < len*len; k++) {
cache_a[k] = A[k];
}
for(unsigned oi = 0; oi < len*len; oi++) {
float sum = 0;
int row = oi % len;
for(int col = 0; col < len; col++) {
unsigned i = (row * len) + col; // 0, 1, 2, 3, 4,...
unsigned j = (col * len) + row; // 0, 3, 6, 9, 1,...
sum += cache_a[i] * cache_a[j];
}
out[oi] = sum;
}
}
As shown in the area report and the system viewer results, preloading the data into local memory reduces the RAM usage by one-third and lowers the latency value from 255 to 97.
Further examination of the area report of matrix_square_v1 shows that the code line int row = oi % len, which is line 30 in the area report below, uses an unusually large amount of area because of the modulus computation.
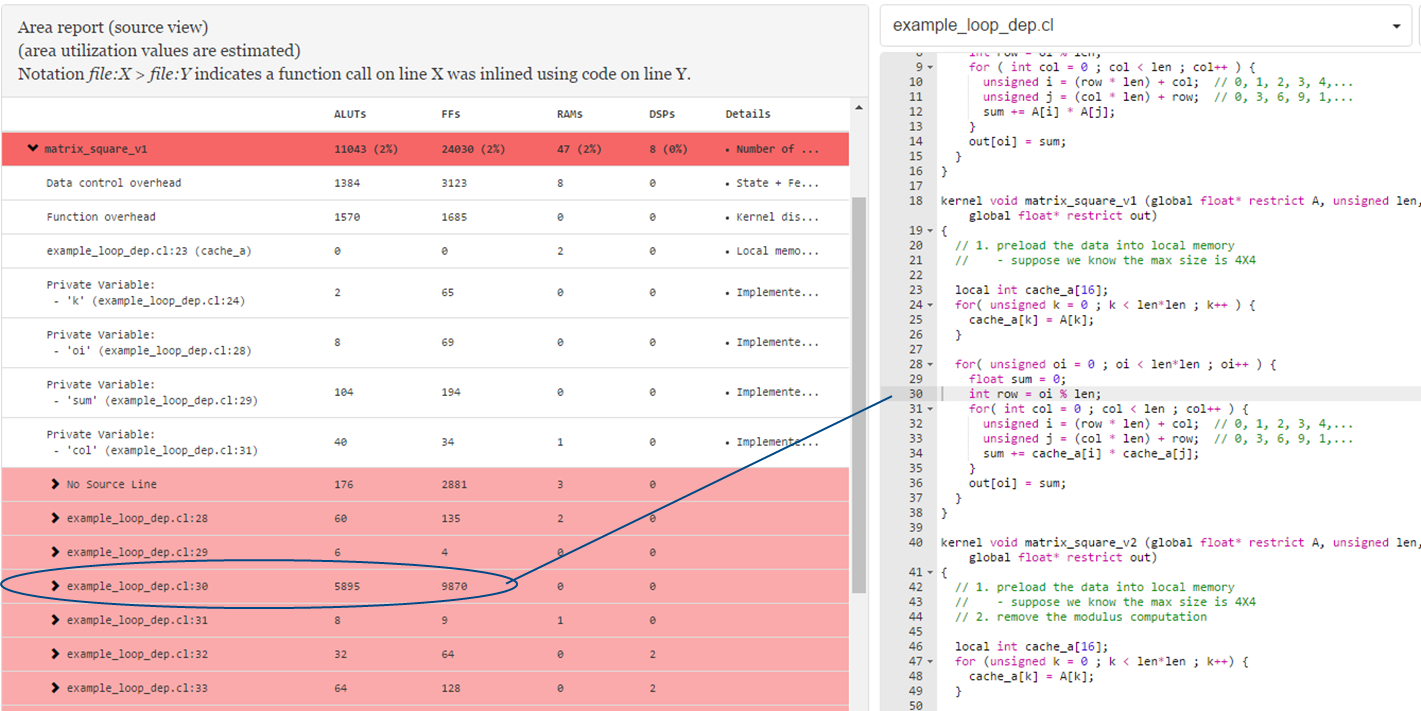
If you remove the modulus computation and replace it with a column counter, as shown in the modified kernel matrix_square_v2, you can reduce the amount of adaptive look-up table (ALUT) and FF usages by 50%.
kernel void matrix_square_v2 (global float* restrict A,
unsigned len,
global float* restrict out)
{
// 1. preload the data into local memory
// - suppose we know the max size is 4X4
// 2. remove the modulus computation
local int cache_a[16];
for (unsigned k = 0; k < len*len; k++) {
cache_a[k] = A[k];
}
unsigned row = 0;
unsigned ci = 0;
for (unsigned oi = 0; oi < len*len; oi++) {
float sum = 0;
// keep a column counter to know when to increment row
if (ci == len) {
ci = 0;
row += 1;
}
ci += 1;
for (int col = 0; col < len; col++) {
unsigned i = (row * len) + col; // 0, 1, 2, 3, 4,...
unsigned j = (col * len) + row; // 0, 3, 6, 9, 1,...
sum += cache_a[i] * cache_a[j];
}
out[oi] = sum;
}
}
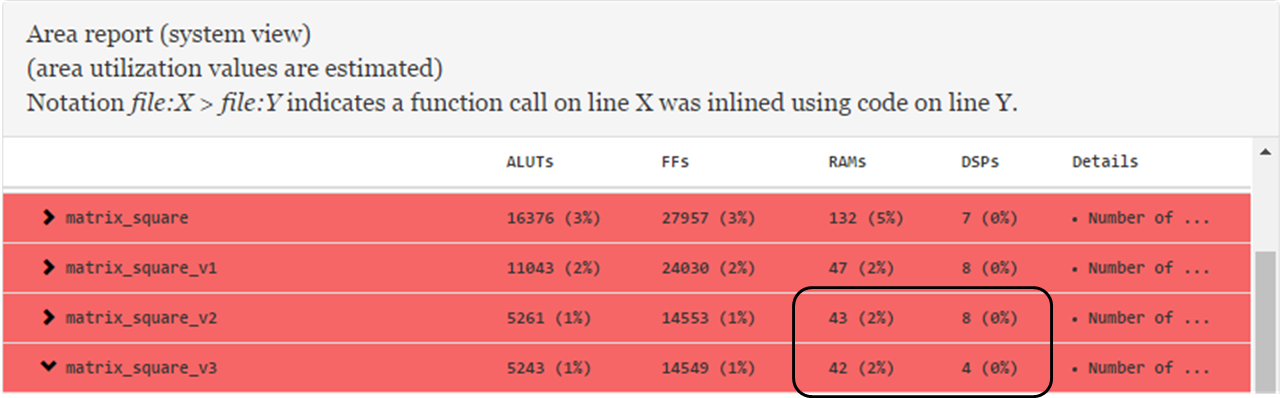
Further examination of the area report of matrix_square_v2 reveals that the computations for indexes i and j (that is, unsigned i = (row * len) + col and unsigned j = (col * len) + row, respectively) have very different ALUT and FF usage estimations. In addition, the area report also shows that these two computations uses digital signal processing (DSP) blocks.

A way to optimize DSP and RAM block usages for index calculation is to remove the multiplication computation and simply keep track of the addition, as shown in the modified kernel matrix_square_v3 below.
kernel void matrix_square_v3 (global float* restrict A,
unsigned len,
global float* restrict out) {
// 1. preload the data into local memory
// - suppose we know the max size is 4X4
// 2. remove the modulus computation
// 3. remove DSP and RAM blocks for index calculation helps reduce the latency
local int cache_a[16];
for (unsigned k = 0; k < len*len; k++) {
cache_a[k] = A[k];
}
unsigned row_i = 0;
unsigned row_j = 0;
unsigned ci = 0;
for (unsigned oi = 0; oi < len*len; oi++) {
float sum = 0;
unsigned i, j;
// keep a column counter to know when to increment row
if (ci == len) {
ci = 0;
row_i += len;
row_j += 1;
}
ci += 1;
i = row_i; // initialize i and j
j = row_j;
for (int col = 0; col < len; col++) {
i += 1; // 0, 1, 2, 3, 0,...
j += len; // 0, 3, 6, 9, 1,...
sum += cache_a[i] * cache_a[j];
}
out[oi] = sum;
}
}By removing the multiplication step, you can reduce DSP usage by 50%, as shown in the area report below. In addition, the modification helps reduce latency.
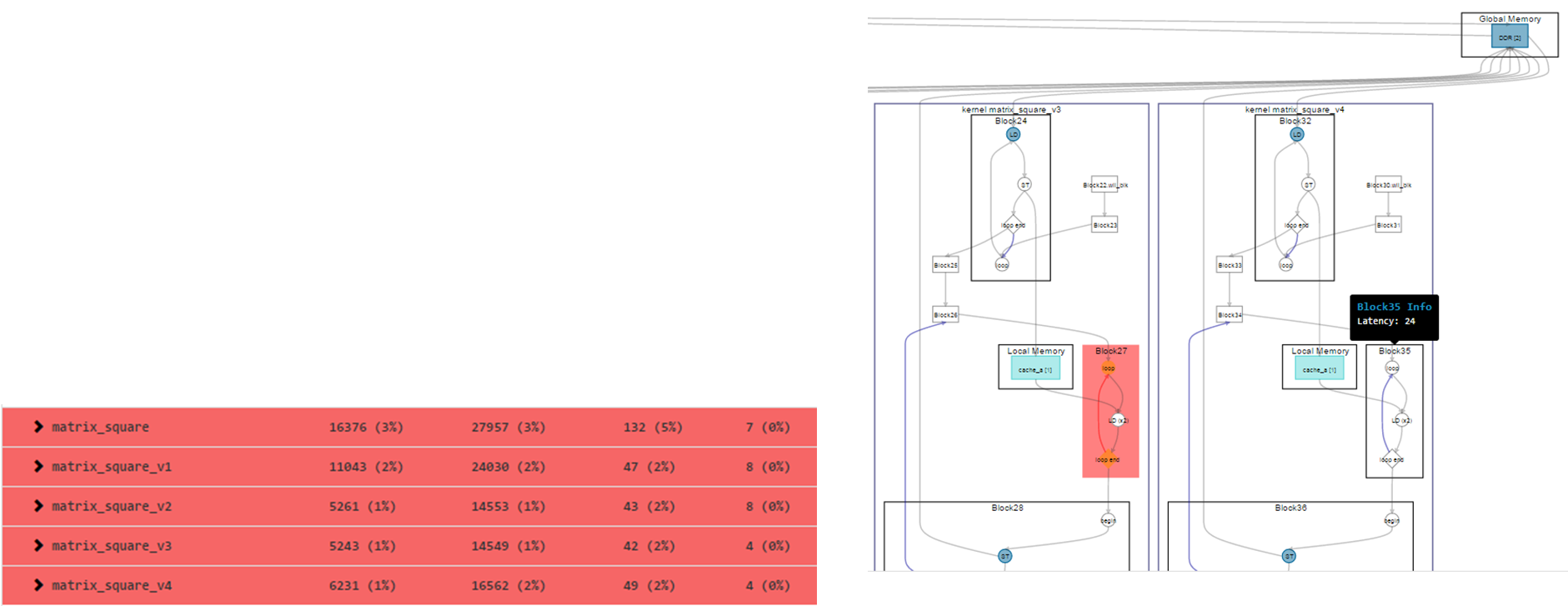
To further reduce latency, you can review the loop analysis report of the modified kernel matrix_square_v3. As shown below, the analysis pane and the details pane of the report indicate that the line sum += cache_a[i] * cache_a[j] has a loop-carried dependency, causing Block27 to have an II bottleneck.

To resolve the loop-carried dependency, you can separate the multiplication and the addition portions of the computation, as shown in the highlighted code below in the modified kernel matrix_square_v4.
kernel void matrix_square_v4 (global float* restrict A,
unsigned len,
global float* restrict out)
{
// 1. preload the data into local memory
// - suppose we know the max size is 4X4
// 2. remove the modulus computation
// 3. remove DSP and RAM blocks for index calculation helps reduce the latency
// 4. remove loop-carried dependency 'sum' to improve throughput by trading off area
local int cache_a[16];
for (unsigned k = 0; k < len*len; k++) {
cache_a[k] = A[k];
}
unsigned row_i = 0;
unsigned row_j = 0;
unsigned ci = 0;
for (unsigned oi = 0; oi < len*len; oi++) {
float sum = 0;
unsigned i, j;
float prod[4]; // make register
#pragma unroll
for (unsigned k = 0; k < 4; k++) {
prod[k] = 0;
}
// keep a column counter to know when to increment row
if (ci == len) {
ci = 0;
row_i += len;
row_j += 1;
}
ci += 1;
i = row_i; // initialize i and j
j = row_j;
for (int col = 0; col < len; col++) {
i += 1; // 0, 1, 2, 3, 0,...
j += len; // 0, 3, 6, 9, 1,...
prod[col] = cache_a[i] * cache_a[j];
}
sum = prod[0];
#pragma unroll
for (unsigned k = 1; k < 4; k++) {
sum += prod[k];
}
out[oi] = sum;
}
}As shown in the area report and system viewer results below, by breaking up the computation steps, you can achieve higher throughput at the expense of increased area usage. The modification also reduces the II value of the loops to 1, and reduces the latency from 30 to 24.