Intel® FPGA SDK for OpenCL™ Pro Edition: Best Practices Guide
6.1.2. Relaxing Loop-Carried Dependency
Consider the following code example:
1 #define N 128
2
3 __kernel void unoptimized (__global float * restrict A,
4 __global float * restrict result)
5 {
6 float mul = 1.0f;
7
8 for (unsigned i = 0; i < N; i++)
9 mul *= A[i];
10
11 * result = mul;
12 }
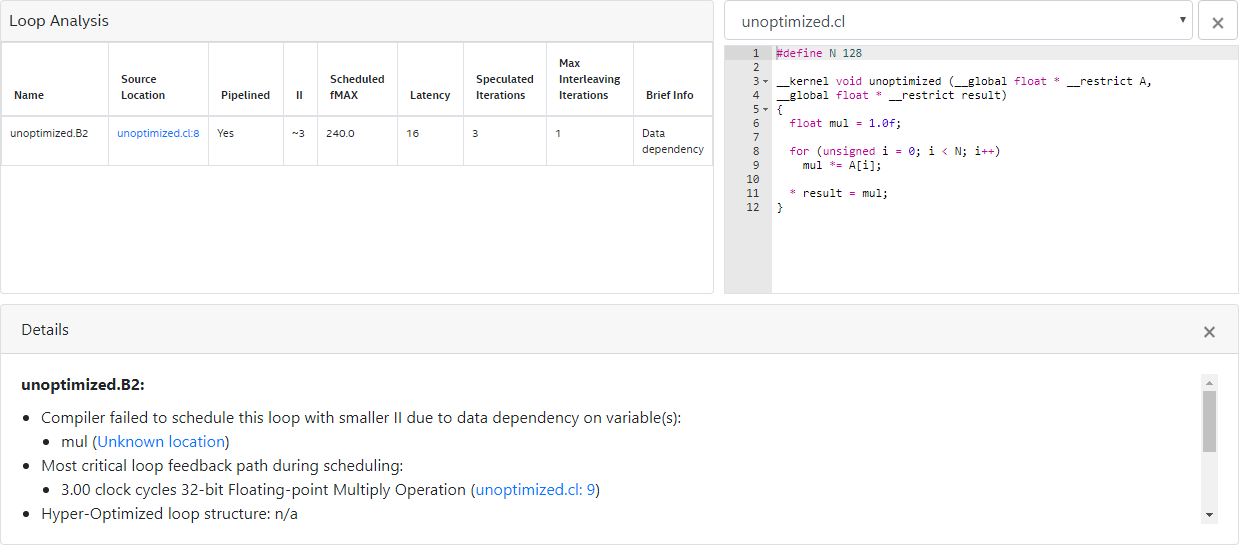
The optimization report above shows that the Intel® FPGA SDK for OpenCL™ Offline Compiler infers pipelined execution for the loop successfully. However, the loop-carried dependency on the variable mul causes loop iterations to launch every six cycles. In this case, the floating-point multiplication operation on line 9 (that is, mul *= A[i]) contributes the largest delay to the computation of the variable mul.
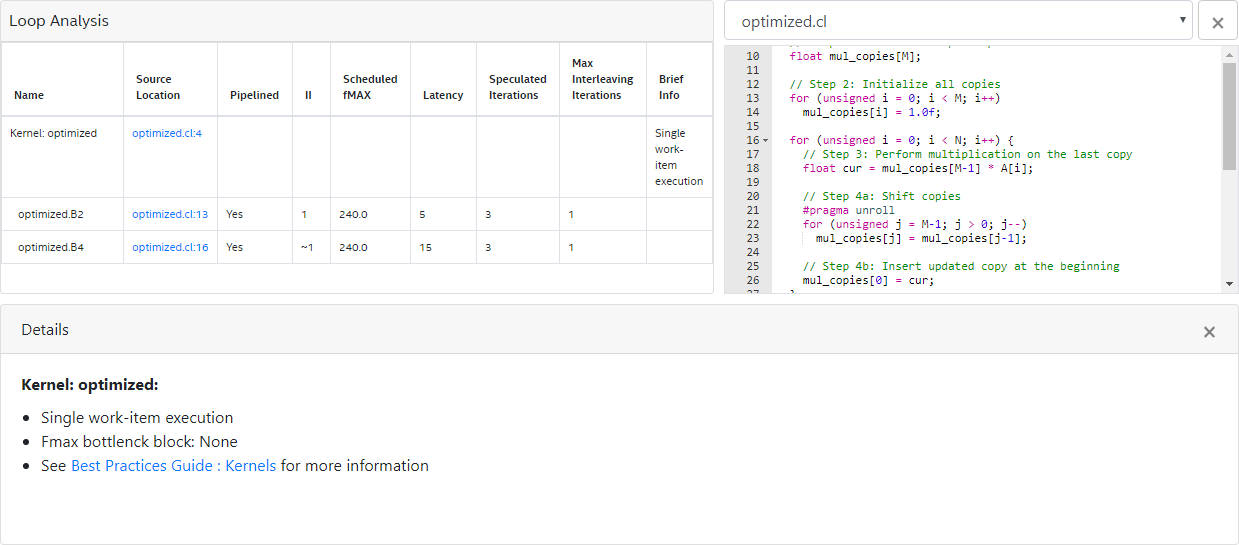
To relax the loop-carried data dependency, instead of using a single variable to store the multiplication results, operate on M copies of the variable and use one copy every M iterations:
- Declare multiple copies of the variable mul (for example, in an array called mul_copies).
- Initialize all the copies of mul_copies.
- Use the last copy in the array in the multiplication operation.
- Perform a shift operation to pass the last value of the array back to the beginning of the shift register.
- Reduce all the copies to mul and write the final value to result.
1 #define N 128
2 #define M 8
3
4 __kernel void optimized (__global float * restrict A,
5 __global float * restrict result)
6 {
7 float mul = 1.0f;
8
9 // Step 1: Declare multiple copies of variable mul
10 float mul_copies[M];
11
12 // Step 2: Initialize all copies
13 for (unsigned i = 0; i < M; i++)
14 mul_copies[i] = 1.0f;
15
16 for (unsigned i = 0; i < N; i++) {
17 // Step 3: Perform multiplication on the last copy
18 float cur = mul_copies[M-1] * A[i];
19
20 // Step 4a: Shift copies
21 #pragma unroll
22 for (unsigned j = M-1; j > 0; j--)
23 mul_copies[j] = mul_copies[j-1];
24
25 // Step 4b: Insert updated copy at the beginning
26 mul_copies[0] = cur;
27 }
28
29 // Step 5: Perform reduction on copies
30 #pragma unroll
31 for (unsigned i = 0; i < M; i++)
32 mul *= mul_copies[i];
33
34 * result = mul;
35 }An optimization report similar to the one below indicates the successful relaxation of the loop-carried dependency on the variable mul: