?potrs

Developer Reference for Intel® oneAPI Math Kernel Library for C

Download PDF

ID 766684

Date 12/16/2022

Version

Public

A newer version of this document is available. Customers should click here to go to the newest version.

Visible to Intel only — GUID: GUID-2039BD5D-44D1-487A-9B68-87BD46019A5F

View Details

?potrs

Solves a system of linear equations with a Cholesky-factored symmetric (Hermitian) positive-definite coefficient matrix.

Syntax

lapack_int LAPACKE_spotrs (int matrix_layout , char uplo , lapack_int n , lapack_int nrhs , const float * a , lapack_int lda , float * b , lapack_int ldb );

lapack_int LAPACKE_dpotrs (int matrix_layout , char uplo , lapack_int n , lapack_int nrhs , const double * a , lapack_int lda , double * b , lapack_int ldb );

lapack_int LAPACKE_cpotrs (int matrix_layout , char uplo , lapack_int n , lapack_int nrhs , const lapack_complex_float * a , lapack_int lda , lapack_complex_float * b , lapack_int ldb );

lapack_int LAPACKE_zpotrs (int matrix_layout , char uplo , lapack_int n , lapack_int nrhs , const lapack_complex_double * a , lapack_int lda , lapack_complex_double * b , lapack_int ldb );

Include Files

mkl.h

Description

The routine solves for X the system of linear equations A*X = B with a symmetric positive-definite or, for complex data, Hermitian positive-definite matrix A, given the Cholesky factorization of A:

`A = U^TU` for real data, `A = U^HU` for complex data	if `uplo='U'`
`A = LL^T` for real data, `A = LL^H` for complex data	if `uplo='L'`

where L is a lower triangular matrix and U is upper triangular. The system is solved with multiple right-hand sides stored in the columns of the matrix B.

Before calling this routine, you must call ?potrf to compute the Cholesky factorization of A.

Input Parameters

matrix_layout	Specifies whether matrix storage layout is row major (LAPACK_ROW_MAJOR) or column major (LAPACK_COL_MAJOR).
uplo	Must be 'U' or 'L'. Indicates how the input matrix `A` has been factored: If `uplo = 'U'`, `U` is stored, where`A` = `U`^T`U` for real data, `A` = `U`^H`U` for complex data. If `uplo = 'L'`, `L` is stored, where`A` = `L``L`^T for real data, `A` = `L``L`^H for complex data.
n	The order of matrix `A`; `n`≥ 0.
nrhs	The number of right-hand sides (`nrhs`≥ 0).
a	Array `A` of size at least max(1, lda*n) The array `a` contains the factor `U` or `L` (see `uplo`) as returned by potrf. .
lda	The leading dimension of `a`. `lda≥ max(1, n).`
b	The array `b` contains the matrix `B` whose columns are the right-hand sides for the systems of equations. The size of `b` must be at least max(1, ldbnrhs) for column major layout and max(1, ldbn) for row major layout.
ldb	The leading dimension of `b`. `ldb`≥ max(1, n) for column major layout and `ldb`≥nrhs for row major layout.

Output Parameters

b	Overwritten by the solution matrix `X`.

Return Values

This function returns a value info.

If info = 0, the execution is successful.

If info = -i, parameter i had an illegal value.

Application Notes

If uplo = 'U', the computed solution for each right-hand side b is the exact solution of a perturbed system of equations (A + E)x = b, where

|E| ≤
					c(n)ε |U
					^H||U|

c(n) is a modest linear function of n, and ε is the machine precision.

A similar estimate holds for uplo = 'L'. If x₀ is the true solution, the computed solution x satisfies this error bound:

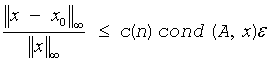
where cond(A,x)= || |A^-1||A| |x| ||_∞ / ||x||_∞≤ ||A^-1||_∞ ||A||_∞ = κ_∞(A).

Note that cond(A,x) can be much smaller than κ_∞ (A). The approximate number of floating-point operations for one right-hand side vector b is 2n² for real flavors and 8n² for complex flavors.

To estimate the condition number κ_∞(A), call ?pocon.

To refine the solution and estimate the error, call ?porfs.

Parent topic: Solving Systems of Linear Equations: LAPACK Computational Routines

Select Your Language

Using Intel.com Search

Quick Links

Recent Searches

Advanced Search

Only search in

Developer Reference for Intel® oneAPI Math Kernel Library for C

?potrs

See Also