Singular Value Decomposition: LAPACK Computational Routines

Developer Reference for Intel® oneAPI Math Kernel Library for C

Download PDF

ID 766684

Date 12/16/2022

Version

Public

A newer version of this document is available. Customers should click here to go to the newest version.

Visible to Intel only — GUID: GUID-31E03413-9B5E-4F72-A4B0-743AFD7E387F

View Details

Singular Value Decomposition: LAPACK Computational Routines

This topic describes LAPACK routines for computing the singular value decomposition (SVD) of a general m-by-n matrix A:

A = UΣV^H.

In this decomposition, U and V are unitary (for complex A) or orthogonal (for real A); Σ is an m-by-n diagonal matrix with real diagonal elements σ_i:

σ₁≥σ₂≥ ... ≥σ_{min(m, n)}≥ 0.

The diagonal elements σ_i are singular values of A. The first min(m, n) columns of the matrices U and V are, respectively, left and right singular vectors of A. The singular values and singular vectors satisfy

Av_i = σ_iu_i and A^Hu_i = σ_iv_i

where u_i and v_i are the i-th columns of U and V, respectively.

To find the SVD of a general matrix A, call the LAPACK routine ?gebrd or ?gbbrd for reducing A to a bidiagonal matrix B by a unitary (orthogonal) transformation: A = QBP^H. Then call ?bdsqr, which forms the SVD of a bidiagonal matrix: B = U₁ΣV₁^H.

Thus, the sought-for SVD of A is given by A = UΣV^H =(QU₁)Σ(V₁^HP^H).

Table "Computational Routines for Singular Value Decomposition (SVD)" lists LAPACK routines that perform singular value decomposition of matrices.

Computational Routines for Singular Value Decomposition (SVD)
Operation	Real matrices	Complex matrices
Reduce `A` to a bidiagonal matrix `B`: `A = QBP^H` (full storage)	?gebrd	?gebrd
Reduce `A` to a bidiagonal matrix `B`: `A = QBP^H` (band storage)	?gbbrd	?gbbrd
Generate the orthogonal (unitary) matrix `Q` or P	?orgbr	?ungbr
Apply the orthogonal (unitary) matrix `Q` or P	?ormbr	?unmbr
Form singular value decomposition of the bidiagonal matrix `B`: `B = UΣV^H`	?bdsqr ?bdsdc	?bdsqr

Decision Tree: Singular Value Decomposition

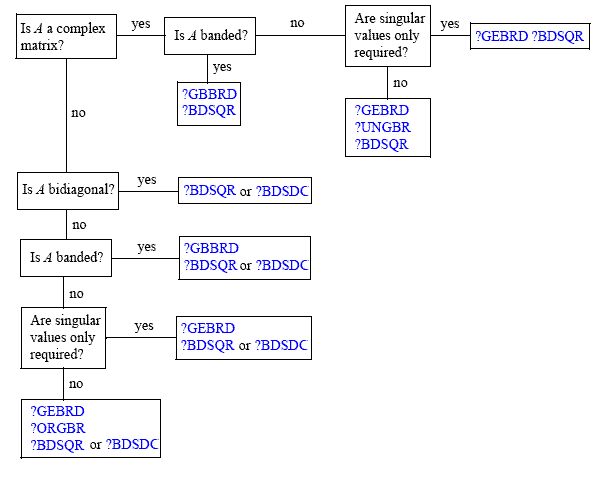
Figure "Decision Tree: Singular Value Decomposition" presents a decision tree that helps you choose the right sequence of routines for SVD, depending on whether you need singular values only or singular vectors as well, whether A is real or complex, and so on.

You can use the SVD to find a minimum-norm solution to a (possibly) rank-deficient least squares problem of minimizing ||Ax - b||². The effective rank k of the matrix A can be determined as the number of singular values which exceed a suitable threshold. The minimum-norm solution is

x = V_k(Σ_k)^-1c

where Σ_k is the leading k-by-k submatrix of Σ, the matrix V_k consists of the first k columns of V = PV₁, and the vector c consists of the first k elements of U^Hb = U₁^HQ^Hb.

Select Your Language

Using Intel.com Search

Quick Links

Recent Searches

Advanced Search

Only search in

Developer Reference for Intel® oneAPI Math Kernel Library for C

Singular Value Decomposition: LAPACK Computational Routines