?geqrt3

Developer Reference for Intel® oneAPI Math Kernel Library for C

Download PDF

ID 766684

Date 12/16/2022

Version

Public

A newer version of this document is available. Customers should click here to go to the newest version.

Visible to Intel only — GUID: GUID-15376C45-AC63-4D61-A6F5-2C5EEE8BC82A

View Details

?geqrt3

Recursively computes a QR factorization of a general real or complex matrix using the compact WY representation of Q.

Syntax

lapack_int LAPACKE_sgeqrt3 (int matrix_layout , lapack_int m , lapack_int n , float * a , lapack_int lda , float * t , lapack_int ldt );

lapack_int LAPACKE_dgeqrt3 (int matrix_layout , lapack_int m , lapack_int n , double * a , lapack_int lda , double * t , lapack_int ldt );

lapack_int LAPACKE_cgeqrt3 (int matrix_layout , lapack_int m , lapack_int n , lapack_complex_float * a , lapack_int lda , lapack_complex_float * t , lapack_int ldt );

lapack_int LAPACKE_zgeqrt3 (int matrix_layout , lapack_int m , lapack_int n , lapack_complex_double * a , lapack_int lda , lapack_complex_double * t , lapack_int ldt );

Include Files

mkl.h

Description

The strictly lower triangular matrix V contains the elementary reflectors H(i) in the ith column below the diagonal. For example, if m=5 and n=3, the matrix V is

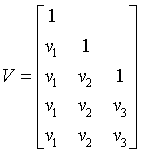
where v_i represents one of the vectors that define H(i). The vectors are returned in the lower part of triangular array a.

NOTE:

The 1s along the diagonal of V are not stored in a.

The block reflector H is then given by

H = I - V*T*V^T for real flavors, and

H = I - V*T*V^H for complex flavors,

where V^T is the transpose and V^His the conjugate transpose of V.

Input Parameters

m: The number of rows in the matrix A (m ≥ n).
n: The number of columns in A (n ≥ 0).
a: Array, size at least max(1, lda*n) for column major and max(1, lda*m) for row major layout. Array a contains the m-by-n matrix A.
lda: The leading dimension of a; at least max(1, m) for column major layout and max(1,n) for row major layout.
ldt: The leading dimension of t; at least max(1, n).

Output Parameters

a

The elements on and above the diagonal of the array contain the n-by-n upper triangular matrix R. The elements below the diagonal are the columns of V.

t

Array, size ldt by n.

The n-by-n upper triangular factor of the block reflector. The elements on and above the diagonal contain the block reflector T. The elements below the diagonal are not used.

Return Values

This function returns a value info.

If info = 0, the execution is successful.

If info < 0 and info = -i, the ith argument had an illegal value.

If info = -1011, memory allocation error occurred.

Parent topic: LAPACK Auxiliary Routines

Select Your Language

Using Intel.com Search

Quick Links

Recent Searches

Advanced Search

Only search in

Developer Reference for Intel® oneAPI Math Kernel Library for C

?geqrt3