mkl_?spffrt2, mkl

Developer Reference for Intel® oneAPI Math Kernel Library for C

Download PDF

ID 766684

Date 12/16/2022

Version

Public

A newer version of this document is available. Customers should click here to go to the newest version.

Visible to Intel only — GUID: GUID-7C6574A1-164E-4A4A-A0F9-75949A5B35F7

View Details

mkl_?spffrt2, mkl_?spffrtx

Computes the partial LDL^T factorization of a symmetric matrix using packed storage.

Syntax

void mkl_sspffrt2 (float *ap , const MKL_INT *n , const MKL_INT *ncolm , float *work , float *work2 );

void mkl_dspffrt2 (double *ap , const MKL_INT *n , const MKL_INT *ncolm , double *work , double *work2 );

void mkl_cspffrt2 (MKL_Complex8 *ap , const MKL_INT *n , const MKL_INT *ncolm , MKL_Complex8 *work , MKL_Complex8 *work2 );

void mkl_zspffrt2 (MKL_Complex16 *ap , const MKL_INT *n , const MKL_INT *ncolm , MKL_Complex16 *work , MKL_Complex16 *work2 );

void mkl_sspffrtx (float *ap , const MKL_INT *n , const MKL_INT *ncolm , float *work , float *work2 );

void mkl_dspffrtx (double *ap , const MKL_INT *n , const MKL_INT *ncolm , double *work , double *work2 );

void mkl_cspffrtx (MKL_Complex8 *ap , const MKL_INT *n , const MKL_INT *ncolm , MKL_Complex8 *work , MKL_Complex8 *work2 );

void mkl_zspffrtx (MKL_Complex16 *ap , const MKL_INT *n , const MKL_INT *ncolm , MKL_Complex16 *work , MKL_Complex16 *work2 );

Include Files

mkl.h

Description

The routine computes the partial factorization A = LDL^T , where L is a lower triangular matrix and D is a diagonal matrix.

CAUTION:

The routine assumes that the matrix A is factorizable. The routine does not perform pivoting and does not handle diagonal elements which are zero, which cause the routine to produce incorrect results without any indication.

Consider the matrix

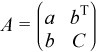
, where a is the element in the first row and first column of A, b is a column vector of size n - 1 containing the elements from the second through n-th column of A, C is the lower-right square submatrix of A, and I is the identity matrix.

The mkl_?spffrt2 routine performs ncolm successive factorizations of the form

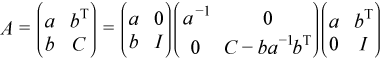
The mkl_?spffrtx routine performs ncolm successive factorizations of the form

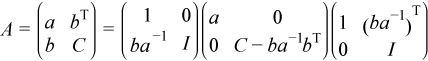
The approximate number of floating point operations performed by real flavors of these routines is (1/6)*ncolm*(2*ncolm² - 6*ncolm*n + 3*ncolm + 6*n² - 6*n + 7).

The approximate number of floating point operations performed by complex flavors of these routines is (1/3)*ncolm*(4*ncolm² - 12*ncolm*n + 9*ncolm + 12*n² - 18*n + 8).

Input Parameters

ap	Array, size at least max(1, `n`(`n`+1)/2). The array `ap` contains the lower triangular part of the matrix `A` in packed storage (see Matrix Storage Schemes for uplo = `'L'`).
n	The order of matrix `A`; `n`≥ 0.
ncolm	The number of columns to factor, ncolm≤n.
work, work2	Workspace arrays, size of each at least n.

Output Parameters

Overwritten by the factor L. The first ncolm diagonal elements of the input matrix A are replaced with the diagonal elements of D. The subdiagonal elements of the first ncolm columns are replaced with the corresponding elements of L. The rest of the input array is updated as indicated in the Description section.

NOTE:

Specifying ncolm = n results in complete factorization A = LDL^T.

Parent topic: Matrix Factorization: LAPACK Computational Routines

Select Your Language

Using Intel.com Search

Quick Links

Recent Searches

Advanced Search

Only search in

Developer Reference for Intel® oneAPI Math Kernel Library for C

mkl_?spffrt2, mkl_?spffrtx

See Also