p?gebal

Developer Reference for Intel® oneAPI Math Kernel Library for C

Download PDF

ID 766684

Date 12/16/2022

Version

Public

A newer version of this document is available. Customers should click here to go to the newest version.

Visible to Intel only — GUID: GUID-62E9F1AE-AE64-4AE3-AB97-B5FA63F17E4A

View Details

p?gebal

Balances a general real/complex matrix.

Syntax

void psgebal(char* job, MKL_INT* n, float* a, MKL_INT* desca, MKL_INT* ilo, MKL_INT* ihi, float* scale, MKL_INT* info);

void pdgebal(char* job, MKL_INT* n, double* a, MKL_INT* desca, MKL_INT* ilo, MKL_INT* ihi, double* scale, MKL_INT* info);

void pcgebal(char* job, MKL_INT* n, complex float* a, MKL_INT* desca, MKL_INT* ilo, MKL_INT* ihi, float* scale, MKL_INT* info);

void pzgebal(char* job, MKL_INT* n, complex double* a, MKL_INT* desca, MKL_INT* ilo, MKL_INT* ihi, double* scale, MKL_INT* info);

Include Files

mkl_scalapack.h

Description

p?gebal balances a general real/complex matrix A. This involves, first, permuting A by a similarity transformation to isolate eigenvalues in the first 1 to ilo-1 and last ihi+1 to n elements on the diagonal; and second, applying a diagonal similarity transformation to rows and columns ilo to ihi to make the rows and columns as close in norm as possible. Both steps are optional.

Balancing may reduce the 1-norm of the matrix, and improve the accuracy of the computed eigenvalues and/or eigenvectors.

Input Parameters

job

(global )

Specifies the operations to be performed on a:

= 'N': none: simply set ilo = 1, ihi = n, scale[i] = 1.0 for i = 0,...,n-1;

= 'P': permute only;

= 'S': scale only;

= 'B': both permute and scale.

n

(global )

The order of the matrix A (n≥ 0).

a

(local ) Pointer into the local memory to an array of size lld_a * LOC_c(n)

This array contains the local pieces of global input matrix A.

desca

(global and local) array of size dlen_.

The array descriptor for the distributed matrix A.

OUTPUT Parameters

a

On exit, a is overwritten by the balanced matrixA.

If job = 'N', a is not referenced.

See Notes for further details.

ilo, ihi

(global )

ilo and ihi are set to integers such that on exit matrix elements A(i,j) are zero if i > j and j = 1,...,ilo-1 or i = ihi+1,...,n.

If job = 'N' or 'S', ilo = 1 and ihi = n.

scale

(global ) array of size n.

Details of the permutations and scaling factors applied to a. If pj is the index of the row and column interchanged with row and column j and dj is the scaling factor applied to row and column j, then

scale[j-1] = pj for j = 1,...,ilo-1, ihi+1,..., n

scale[j-1] = dj for j = ilo,...,ihi

The order in which the interchanges are made is n to ihi+1, then 1 to ilo-1.

info

(global )

= 0: successful exit.

< 0: if info = -i, the i-th argument had an illegal value.

Application Notes

The permutations consist of row and column interchanges which put the matrix in the form

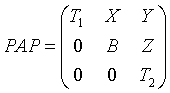
where T1 and T2 are upper triangular matrices whose eigenvalues lie along the diagonal. The column indices ilo and ihi mark the starting and ending columns of the submatrix B. Balancing consists of applying a diagonal similarity transformation D^-1BD to make the 1-norms of each row of B and its corresponding column nearly equal. The output matrix is

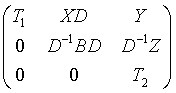
Information about the permutations P and the diagonal matrix D is returned in the vector scale.

Parent topic: ScaLAPACK Auxiliary Routines

Select Your Language

Using Intel.com Search

Quick Links

Recent Searches

Advanced Search

Only search in

Developer Reference for Intel® oneAPI Math Kernel Library for C

p?gebal

See Also