?sytrf_rook

Developer Reference for Intel® oneAPI Math Kernel Library for C

Download PDF

ID 766684

Date 12/16/2022

Version

Public

A newer version of this document is available. Customers should click here to go to the newest version.

Visible to Intel only — GUID: GUID-E4F0C583-4A62-4B8C-8035-580C08F2F9BC

View Details

?sytrf_rook

Computes the bounded Bunch-Kaufman factorization of a symmetric matrix.

Syntax

lapack_int LAPACKE_ssytrf_rook (int matrix_layout, char uplo, lapack_int n, float * a, lapack_int lda, lapack_int * ipiv);

lapack_int LAPACKE_dsytrf_rook (int matrix_layout, char uplo, lapack_int n, double * a, lapack_int lda, lapack_int * ipiv);

lapack_int LAPACKE_csytrf_rook (int matrix_layout, char uplo, lapack_int n, lapack_complex_float * a, lapack_int lda, lapack_int * ipiv);

lapack_int LAPACKE_zsytrf_rook (int matrix_layout, char uplo, lapack_int n, lapack_complex_double * a, lapack_int lda, lapack_int * ipiv);

Include Files

mkl.h

Description

The routine computes the factorization of a real/complex symmetric matrix A using the bounded Bunch-Kaufman ("rook") diagonal pivoting method. The form of the factorization is:

if uplo='U', A = U*D*U^T
if uplo='L', A = L*D*L^T,

where A is the input matrix, U and L are products of permutation and triangular matrices with unit diagonal (upper triangular for U and lower triangular for L), and D is a symmetric block-diagonal matrix with 1-by-1 and 2-by-2 diagonal blocks. U and L have 2-by-2 unit diagonal blocks corresponding to the 2-by-2 blocks of D.

Input Parameters

matrix_layout	Specifies whether matrix storage layout for array b is row major (LAPACK_ROW_MAJOR) or column major (LAPACK_COL_MAJOR).
uplo	Must be 'U' or 'L'. Indicates whether the upper or lower triangular part of `A` is stored and how `A` is factored: If `uplo = 'U'`, the array `a` stores the upper triangular part of the matrix `A`, and `A` is factored as `UDU^T`. If `uplo = 'L'`, the array `a` stores the lower triangular part of the matrix `A`, and `A` is factored as `LDL^T`.
n	The order of matrix `A`; `n`≥ 0.
a	Array, size lda*n. The array `a` contains either the upper or the lower triangular part of the matrix `A` (see `uplo`).
lda	The leading dimension of `a`; at least `max(1, n)`.

Output Parameters

The upper or lower triangular part of a is overwritten by details of the block-diagonal matrix D and the multipliers used to obtain the factor U (or L).

ipiv

If ipiv(k) > 0, then rows and columns k and ipiv(k) were interchanged and D_{k, k} is a 1-by-1 diagonal block.

If uplo = 'U' and ipiv(k) < 0 and ipiv(k - 1) < 0, then rows and columns k and -ipiv(k) were interchanged, rows and columns k - 1 and -ipiv(k - 1) were interchanged, and D_{k-1:k, k-1:k} is a 2-by-2 diagonal block.

If uplo = 'L' and ipiv(k) < 0 and ipiv(k + 1) < 0, then rows and columns k and -ipiv(k) were interchanged, rows and columns k + 1 and -ipiv(k + 1) were interchanged, and D_{k:k+1, k:k+1} is a 2-by-2 diagonal block.

Return Values

This function returns a value info.

If info = 0, the execution is successful.

If info = -i, the i-th parameter had an illegal value.

If info = i, D_ii is 0. The factorization has been completed, but D is exactly singular. Division by 0 will occur if you use D for solving a system of linear equations.

Application Notes

The total number of floating-point operations is approximately (1/3)n³ for real flavors or (4/3)n³ for complex flavors.

After calling this routine, you can call the following routines:

?sytrs_rook	to solve `A*X = B`
?sycon_rook (Fortran only)	to estimate the condition number of `A`
?sytri_rook (Fortran only)	to compute the inverse of `A`.

If uplo = 'U', then A = U*D*U', where

U = P(n)*U(n)* ... *P(k)*U(k)*...,

that is, U is a product of terms P(k)*U(k), where

k decreases from n to 1 in steps of 1 and 2.
D is a block diagonal matrix with 1-by-1 and 2-by-2 diagonal blocks D(k).
P(k) is a permutation matrix as defined by ipiv[k-1].
U(k) is a unit upper triangular matrix, such that if the diagonal block D(k) is of order s (s = 1 or 2), then

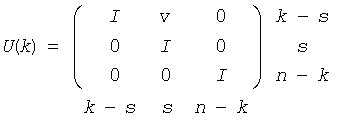
If s = 1, D(k) overwrites A(k,k), and v overwrites A(1:k-1,k).

If s = 2, the upper triangle of D(k) overwrites A(k-1,k-1), A(k-1,k) and A(k,k), and v overwrites A(1:k-2,k -1:k).

If uplo = 'L', then A = L*D*L', where

L = P(1)*L(1)* ... *P(k)*L(k)*...,

that is, L is a product of terms P(k)*L(k), where

k increases from 1 to n in steps of 1 and 2.
D is a block diagonal matrix with 1-by-1 and 2-by-2 diagonal blocks D(k).
P(k) is a permutation matrix as defined by ipiv(k).
L(k) is a unit lower triangular matrix, such that if the diagonal block D(k) is of order s (s = 1 or 2), then

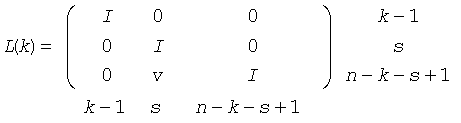
If s = 1, D(k) overwrites A(k,k), and v overwrites A(k+1:n,k).

If s = 2, the lower triangle of D(k) overwrites A(k,k), A(k+1,k), and A(k+1,k+1), and v overwrites A(k+2:n,k:k+1).

Parent topic: Matrix Factorization: LAPACK Computational Routines

Select Your Language

Using Intel.com Search

Quick Links

Recent Searches

Advanced Search

Only search in

Developer Reference for Intel® oneAPI Math Kernel Library for C

?sytrf_rook

See Also