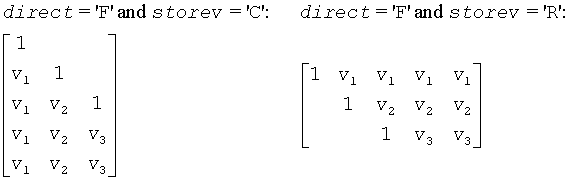?larfb

Developer Reference for Intel® oneAPI Math Kernel Library for C

Download PDF

ID 766684

Date 12/16/2022

Version

Public

A newer version of this document is available. Customers should click here to go to the newest version.

Visible to Intel only — GUID: GUID-15B732D8-02BD-4C77-B822-0CA713C3E7A4

View Details

?larfb

Applies a block reflector or its transpose/conjugate-transpose to a general rectangular matrix.

Syntax

lapack_int LAPACKE_slarfb (int matrix_layout , char side , char trans , char direct , char storev , lapack_int m , lapack_int n , lapack_int k , const float * v , lapack_int ldv , const float * t , lapack_int ldt , float * c , lapack_int ldc );

lapack_int LAPACKE_dlarfb (int matrix_layout , char side , char trans , char direct , char storev , lapack_int m , lapack_int n , lapack_int k , const double * v , lapack_int ldv , const double * t , lapack_int ldt , double * c , lapack_int ldc );lapack_int LAPACKE_clarfb (int matrix_layout , char side , char trans , char direct , char storev , lapack_int m , lapack_int n , lapack_int k , const lapack_complex_float * v , lapack_int ldv , const lapack_complex_float * t , lapack_int ldt , lapack_complex_float * c , lapack_int ldc );

lapack_int LAPACKE_zlarfb (int matrix_layout , char side , char trans , char direct , char storev , lapack_int m , lapack_int n , lapack_int k , const lapack_complex_double * v , lapack_int ldv , const lapack_complex_double * t , lapack_int ldt , lapack_complex_double * c , lapack_int ldc );

Include Files

mkl.h

Description

The real flavors of the routine ?larfb apply a real block reflector H or its transpose H^T to a real m-by-n matrix C from either left or right.

The complex flavors of the routine ?larfb apply a complex block reflector H or its conjugate transpose H^H to a complex m-by-n matrix C from either left or right.

Input Parameters

A <datatype> placeholder, if present, is used for the C interface data types in the C interface section above. See C Interface Conventions for the C interface principal conventions and type definitions.

side

If side = 'L': apply H or H^T for real flavors and H or H^H for complex flavors from the left.

If side = 'R': apply H or H^T for real flavors and H or H^H for complex flavors from the right.

trans

If trans = 'N': apply H (No transpose).

If trans = 'C': apply H^H (Conjugate transpose).

If trans = 'T': apply H^T (Transpose).

direct

Indicates how H is formed from a product of elementary reflectors

If direct = 'F': H = H(1)*H(2)*. . . *H(k) (forward)

If direct = 'B': H = H(k)* . . . H(2)*H(1) (backward)

storev

Indicates how the vectors which define the elementary reflectors are stored:

If storev = 'C': Column-wise

If storev = 'R': Row-wise

m

The number of rows of the matrix C.

n

The number of columns of the matrix C.

k

The order of the matrix T (equal to the number of elementary reflectors whose product defines the block reflector).

v

The size limitations depend on values of parameters storev and side as described in the following table:

	`storev` = C		`storev` = R
	`side` = L	`side` = R	`side` = L	`side` = R
Column major	max(1,`ldv`*`k`)	max(1,`ldv`*`k`)	max(1,`ldv`*`m`)	max(1,`ldv`*`n`)
Row major	max(1,`ldv`*`m`)	max(1,`ldv`*`n`)	max(1,`ldv`*`k`)	max(1,`ldv`*`k`)

The matrix v. See Application Notes below.

ldv

The leading dimension of the array v.It should satisfy the following conditions:

	`storev` = C		`storev` = R
	`side` = L	`side` = R	`side` = L	`side` = R
Column major	max(1,`m`)	max(1,`n`)	max(1,`k`)	max(1,`k`)
Row major	max(1,`k`)	max(1,`k`)	max(1,`m`)	max(1,`n`)

t

Array, size at least max(1,ldt * k).

Contains the triangular k-by-k matrix T in the representation of the block reflector.

ldt

The leading dimension of the array t.

ldt≥k.

c

Array, size at least max(1, ldc * n) for column major layout and max(1, ldc * m) for row major layout.

On entry, the m-by-n matrix C.

ldc

The leading dimension of the array c.

ldc≥ max(1,m) for column major layout and ldc≥ max(1,n) for row major layout.

Output Parameters

c

On exit, c is overwritten by the product of the following:

H*C, or H^T*C, or C*H, or C*H^T for real flavors
H*C, or H^H*C, or C*H, or C*H^H for complex flavors

Return Values

This function returns a value info.

If info = 0, the execution is successful.

If info = -i, the i-th parameter had an illegal value.

If info = -1011, memory allocation error occurred.

Application Notes

The shape of the matrix V and the storage of the vectors which define the H(i) is best illustrated by the following example with n = 5 and k = 3. The elements equal to 1 are not stored; the corresponding array elements are modified but restored on exit. The rest of the array is not used.

Parent topic: LAPACK Auxiliary Routines

Select Your Language

Using Intel.com Search

Quick Links

Recent Searches

Advanced Search

Only search in

Developer Reference for Intel® oneAPI Math Kernel Library for C

?larfb