1.15.6. Fractal Synthesis Optimization

Quartus® Prime Pro Edition User Guide: Design Compilation

Download PDF

ID 683236

Date 4/01/2024

Version

Public

A newer version of this document is available. Customers should click here to go to the newest version.

Visible to Intel only — GUID: rxr1533827311846

Ixiasoft

View Details

1.15.6. Fractal Synthesis Optimization

Fractal synthesis optimizations can be useful for deep-learning accelerators and other high-throughput, arithmetic-intensive designs that exceed all available DSP resources. For such designs, fractal synthesis optimization can achieve 20-45% area reduction.

Fractal synthesis is a set of synthesis optimizations that use FPGA resources in an optimal way for arithmetic-intensive designs. These synthesis optimizations consist of multiplier regularization and retiming, as well as continuous arithmetic packing. The optimizations target designs with large numbers of low-precision arithmetic operations (such as additions and multiplications). You can enable fractal synthesis globally or for specific multipliers, as Enabling or Disabling Fractal Synthesis describes.

Project-Wide Fractal Synthesis Considerations

Note: Fractal synthesis optimization is most suitable for designs with deep-learning accelerators or other high-throughput, arithmetic-intensive functions that exceed all DSP resources. Enabling fractal synthesis project-wide can cause unnecessary bloat on modules that are not suitable for fractal optimizations. Consider the following factors before enabling fractal synthesis optimization project wide:

Intel FPGA devices contain thousands of hard DSP blocks that are perfectly suited for arithmetic operations. If the total amount of arithmetic functions in your design is small, then there is no need to enable Fractal Synthesis. In such cases, all the arithmetic functions map directly into DSPs by default. Enable global Fractal Synthesis only if there are not enough DSP blocks available to implement all arithmetic components. Enable Fractal Synthesis only for modules that you do not want the Compiler to map into DSPs.
In the current version of the Quartus® Prime Pro Edition software, fractal synthesis optimizations target low-precision multiplication. Implement high-precision multipliers (where width of every operand exceeds 11 bits) using DSP blocks.
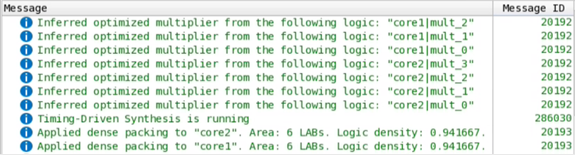
If you enable project-wide Fractal Synthesis, the following information message number 20193 may generate during compilation:
```
Applied dense packing to "<entity>". Area: 2 LABs. Logic density: 0.775.
```
This information indicates the effort the Compiler is packing computational logic into a smaller number of LABs. If the design is already highly utilized, the Compiler can skip this stage.
- Verify that the Area the message reports does not exceed 100 LABs. If the Area exceeds 100 LABs, divide fractal synthesis blocks to sub-blocks, and then assign the fractal synthesis optimizations to the sub-blocks independently.
- Verify that the Logic density the message reports is greater than 0.75. If the logic density is less than 0.75, disable Fractal Synthesis for this entity because standard synthesis typically achieves better density.

Table 33. Fractal Synthesis Area Improvement
		Area (LABs)
Device	Dot-product	Fractal Synthesis ON	Fractal Synthesis OFF
Arria® 10 and Cyclone® 10 GX	Sum of 16 4x4sm	12	19
	Sum of 16 5x5sm	19	32
	Sum of 16 6x6sm	25	36
	Sum of 16 7x7sm	34	44
	Sum of 16 8x8sm	45	60
Stratix® 10 and Agilex™ 7 Devices	Sum of 16 4x4sm	15	22
	Sum of 16 5x5sm	21	39
	Sum of 16 6x6sm	29	47
	Sum of 16 7x7sm	39	55
	Sum of 16 8x8sm	55	71

Multiplier Regularization and Retiming

Multiplier regularization and retiming performs inference of highly optimized soft multiplier implementations. The Compiler may apply backward retiming to two or more pipeline stages if required. When you enable fractal synthesis, the Compiler applies multiplier regularization and retiming to signed and unsigned multipliers.

Figure 127. Multiplier Retiming

Note:

Multiplier regularization uses only logic resources, and does not use DSP blocks.
Multiplier regularization and retiming is applied to both signed and unsigned multipliers in modules where the FRACTAL_SYNTHESIS QSF assignment is set.

Multiplier Regularization Example

The following simple, unsigned dot-product design example contains multiplication operators with 5-bit operands. These short multipliers are perfect candidates for multiplier regularization.

(* altera_attribute = "-name FRACTAL_SYNTHESIS ON" *)
module dot_product(
   input clk,
   input [4:0] a, b, c, d, e, f, g, h,
   output reg [11:0] out
);
reg [9:0] ab, cd, ef, gh;
reg [10:0] ab_cd, ef_gh;

always @(posedge clk)
begin
	ab <= a * b;
	cd <= c * d;
	ef <= e * f;
	gh <= g * h;
	ab_cd <= ab + cd;
	ef_gh <= ef + gh;
	out <= ab_cd + ef_gh;
end
endmodule

module top(
   input clk,
   input [4:0] a1, b1, c1, d1, e1, f1, g1, h1,
   input [4:0] a2, b2, c2, d2, e2, f2, g2, h2,
   output [11:0] out1, out2
);
dot_product core1(.clk(clk), .a(a1), .b(b1), .c(c1), .d(d1), 
    .e(e1), .f(f1), .g(g1), .h(h1), .out(out1));
dot_product core2(.clk(clk), .a(a2), .b(b2), .c(c2), .d(d2), 
	.e(e2), .f(f2), .g(g2), .h(h2), .out(out2));
endmodule

Quartus® Prime synthesis prints the following messages to the console:

Figure 128. Console Messages

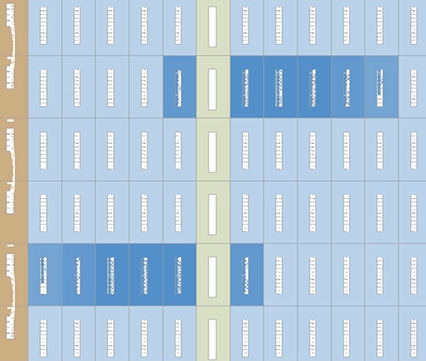
In the Chip Planner, you can observe this design having two unsigned dot-product cores. These cores are independently optimized and placed. The LAB resources are nearly 100% optimized, as the following image shows:

Figure 129. Design Placement

Signed dot-products are common for deep-learning applications. The following demonstrates an example of a signed dot-product:

(* altera_attribute = "-name FRACTAL_SYNTHESIS ON" *)
module dot_product(
   input signed clk,
   input signed [4:0] a, b, c, d, e, f, g, h,
   output reg signed [11:0] out
);
reg signed [9:0] ab, cd, ef, gh;
reg signed [10:0] ab_cd, ef_gh;

always @(posedge clk)
begin
	ab <= a * b;
	cd <= c * d;
	ef <= e * f;
	gh <= g * h;
	ab_cd <= ab + cd;
	ef_gh <= ef + gh;
	out <= ab_cd + ef_gh;
end
endmodule

module top(
   input clk,
   input signed [4:0] a1, b1, c1, d1, e1, f1, g1, h1,
   input signed [4:0] a2, b2, c2, d2, e2, f2, g2, h2,
   output signed [11:0] out1, out2
);
dot_product core1(.clk(clk), .a(a1), .b(b1), .c(c1), .d(d1), 
    .e(e1), .f(f1), .g(g1), .h(h1), .out(out1));
dot_product core2(.clk(clk), .a(a2), .b(b2), .c(c2), .d(d2), 
	.e(e2), .f(f2), .g(g2), .h(h2), .out(out2));
endmodule

Quartus® Prime synthesis displays the following messages in the console:

Figure 130. Console Messages

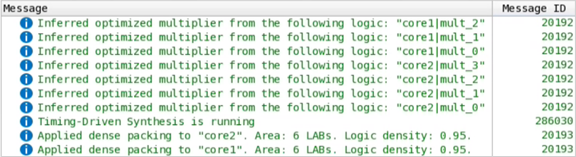
In the Chip Planner, you can observe this design having two signed dot-product cores independently optimized and placed:

Figure 131. Design Placement

Continuous Arithmetic Packing

Continuous arithmetic packing re-synthesizes arithmetic gates into logic blocks optimally sized to fit into Intel® FPGA LABs. This optimization allows up to 100% utilization of LAB resources for the arithmetic blocks.

When you enable fractal synthesis, the Compiler applies this optimization to all carry chains and two-input logic gates. This optimization can pack adder trees, multipliers, and any other arithmetic-related logic.

Figure 132. Continuous Arithmetic Packing

Note that continuous arithmetic packing works independently of multiplier regularization. So, if you are using a multiplier that is not regularized (such as writing your own multiplier) then continuous arithmetic packing can still operate.

Select Your Language

Using Intel.com Search

Quick Links

Recent Searches

Advanced Search

Only search in

Quartus® Prime Pro Edition User Guide: Design Compilation

1.15.6. Fractal Synthesis Optimization

Project-Wide Fractal Synthesis Considerations

Multiplier Regularization and Retiming

Multiplier Regularization Example

Continuous Arithmetic Packing