Intel® oneAPI Data Analytics Library Developer Guide and Reference
A newer version of this document is available. Customers should click here to go to the newest version.
Logistic Regression
This chapter describes the Logistic Regression algorithm implemented in oneDAL.
The Logistic Regression algorithm solves the classification problem and predicts class labels and probabilities of objects belonging to each class.
Operation |
Computational methods |
Programming Interface |
||
Mathematical Formulation
Training
Given n feature vectors 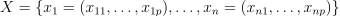 of size p and n responses
of size p and n responses 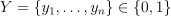 , the problem is to fit the model weights
, the problem is to fit the model weights 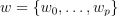 to minimize Logistic Loss
to minimize Logistic Loss 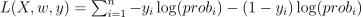 . Where *
. Where * 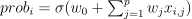 - predicted probabilities, *
- predicted probabilities, * 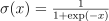 - a sigmoid function. Note that probabilities are binded to interval
- a sigmoid function. Note that probabilities are binded to interval 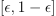 to avoid problems with computing log function (
to avoid problems with computing log function (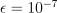 if float type is used and
if float type is used and 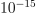 otherwise)
otherwise)
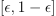 to prevent issues when computing the logarithm function. Where
to prevent issues when computing the logarithm function. Where
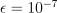 for float type and
for float type and
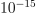 otherwise.
otherwise.
Training Method: dense_batch
Since Logistic Loss is a convex function, you can use one of the iterative solvers designed for convex problems for minimization. During training, the data is divided into batches, and the gradients from each batch are summed up.
Refer to Mathematical formulation: Newton-CG.
Training Method: sparse
Using this method you can train Logistic Regression model on sparse data. All you need is to provide matrix with feature vectors as sparse table. Find more info about sparse tables here Compressed Sparse Rows (CSR) Table:.
Inference
Given r feature vectors 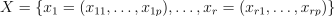 of size p, the problem is to calculate the probabilities of associated with these feature vectors belonging to each class and determine the most probable class label for each object.
of size p, the problem is to calculate the probabilities of associated with these feature vectors belonging to each class and determine the most probable class label for each object.
The probabilities are calculated using this formula 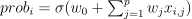 . Where
. Where 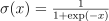 is a sigmoid function. If the probability is bigger than 0.5 then class label is set to 1, otherwise to 0.
is a sigmoid function. If the probability is bigger than 0.5 then class label is set to 1, otherwise to 0.
Programming Interface
Refer to API Reference: Logistic Regression.
Examples: Logistic Regression
oneAPI DPC++
- Batch Processing: