Intel® oneAPI Data Analytics Library Developer Guide and Reference
A newer version of this document is available. Customers should click here to go to the newest version.
Correlation and Variance-Covariance Matrices
Variance-covariance and correlation matrices are among the most important quantitative measures of a data set that characterize statistical relationships involving dependence.
Specifically, the covariance measures the extent to which variables “fluctuate together” (that is, co-vary). The correlation is the covariance normalized to be between -1 and +1. A positive correlation indicates the extent to which variables increase or decrease simultaneously. A negative correlation indicates the extent to which one variable increases while the other one decreases. Values close to +1 and -1 indicate a high degree of linear dependence between variables.
Details
Given a set X of n feature vectors  of dimension p, the problem is to compute the sample means and variance-covariance matrix or correlation matrix:
of dimension p, the problem is to compute the sample means and variance-covariance matrix or correlation matrix:
Statistic |
Definition |
|---|---|
Means |
|
Variance-covariance matrix |
|
Correlation matrix |
|
Computation
The following computation modes are available:
Examples
C++ (CPU)
Batch Processing:
Python*
Batch Processing:
Online Processing:
Distributed Processing:
Performance Considerations
To get the best overall performance when computing correlation or variance-covariance matrices:
If input data is homogeneous, provide the input data and store results in homogeneous numeric tables of the same type as specified in the algorithmFPType class template parameter.
If input data is non-homogeneous, use AOS layout rather than SOA layout.
Product and Performance Information |
|---|
Performance varies by use, configuration and other factors. Learn more at www.Intel.com/PerformanceIndex. Notice revision #20201201 |
 , where
, where 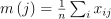
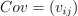 , where
, where 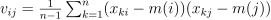 ,
,  ,
, 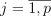
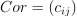 , where
, where 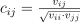 ,
,