?gehd2

Developer Reference for Intel® oneAPI Math Kernel Library for Fortran

Download PDF

ID 766686

Date 3/31/2023

Version

Public

A newer version of this document is available. Customers should click here to go to the newest version.

Visible to Intel only — GUID: GUID-646F2BAE-6D33-4114-B167-B731ED52CCB8

View Details

?gehd2

Reduces a general square matrix to upper Hessenberg form using an unblocked algorithm.

Syntax

call sgehd2( n, ilo, ihi, a, lda, tau, work, info )

call dgehd2( n, ilo, ihi, a, lda, tau, work, info )

call cgehd2( n, ilo, ihi, a, lda, tau, work, info )

call zgehd2( n, ilo, ihi, a, lda, tau, work, info )

Include Files

mkl.fi

Description

The routine reduces a real/complex general matrix A to upper Hessenberg form H by an orthogonal or unitary similarity transformation Q^T*A*Q = H (for real flavors) or Q^H*A*Q = H (for complex flavors).

The routine does not form the matrix Q explicitly. Instead, Q is represented as a product of elementary reflectors.

Input Parameters

n

INTEGER The order of the matrix A (n≥ 0).

ilo, ihi

INTEGER. It is assumed that A is already upper triangular in rows and columns 1:ilo -1 and ihi+1:n.

If A has been output by ?gebal, then

ilo and ihi must contain the values returned by that routine. Otherwise they should be set to ilo = 1 and ihi = n. Constraint: 1 ≤ ilo ≤ ihi ≤ max(1, n).

a, work

REAL for sgehd2

DOUBLE PRECISION for dgehd2

COMPLEX for cgehd2

DOUBLE COMPLEX for zgehd2.

Arrays:

a (lda,*) contains the n-by-n matrix A to be reduced. The second dimension of a must be at least max(1, n).

work (n) is a workspace array.

lda

INTEGER. The leading dimension of a; at least max(1, n).

Output Parameters

a

On exit, the upper triangle and the first subdiagonal of A are overwritten with the upper Hessenberg matrix H and the elements below the first subdiagonal, with the array tau, represent the orthogonal/unitary matrix Q as a product of elementary reflectors. See Application Notes below.

tau

REAL for sgehd2

DOUBLE PRECISION for dgehd2

COMPLEX for cgehd2

DOUBLE COMPLEX for zgehd2.

Array, DIMENSION at least max (1, n-1).

Contains the scalar factors of elementary reflectors. See Application Notes below.

info

INTEGER.

If info = 0, the execution is successful.

If info = -i, the i-th parameter had an illegal value.

Application Notes

The matrix Q is represented as a product of (ihi - ilo) elementary reflectors

Q = H(ilo)*H(ilo +1)*...*H(ihi -1)

Each H(i) has the form

H(i) = I - tau*v*v^T for real flavors, or

H(i) = I - tau*v*v^H for complex flavors

where tau is a real/complex scalar, and v is a real/complex vector with v(1:i) = 0, v(i+1) = 1 and v(ihi+1:n) = 0.

On exit, v(i+2:ihi) is stored in a(i+2:ihi, i) and tau in tau(i).

The contents of a are illustrated by the following example, with n = 7, ilo = 2 and ihi = 6:

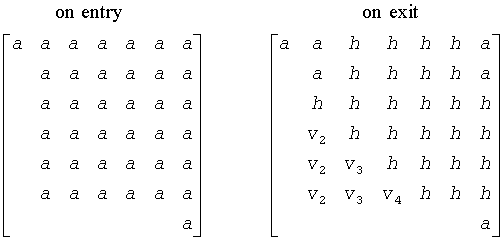
where a denotes an element of the original matrix A, h denotes a modified element of the upper Hessenberg matrix H, and v_i denotes an element of the vector defining H(i).

Parent topic: LAPACK Auxiliary Routines

Select Your Language

Using Intel.com Search

Quick Links

Recent Searches

Advanced Search

Only search in

Developer Reference for Intel® oneAPI Math Kernel Library for Fortran

?gehd2