?getrf2

Developer Reference for Intel® oneAPI Math Kernel Library for Fortran

Download PDF

ID 766686

Date 3/31/2023

Version

Public

A newer version of this document is available. Customers should click here to go to the newest version.

Visible to Intel only — GUID: GUID-04EB4C92-B11E-4BA0-898A-E239C2B5C5E8

View Details

?getrf2

Computes LU factorization using partial pivoting with row interchanges.

Syntax

call sgetrf2 (m, n, a, lda, ipiv, info )

call dgetrf2 (m, n, a, lda, ipiv, info )

call cgetrf2 (m, n, a, lda, ipiv, info )

call zgetrf2 (m, n, a, lda, ipiv, info )

Include Files

mkl.fi

Description

?getrf2 computes an LU factorization of a general m-by-n matrix A using partial pivoting with row interchanges.

The factorization has the form

A = P * L * U

where P is a permutation matrix, L is lower triangular with unit diagonal elements (lower trapezoidal if m > n), and U is upper triangular (upper trapezoidal if m < n).

This is the recursive version of the algorithm. It divides the matrix into four submatrices:

where A11 is n1 by n1 and A22 is n2 by n2 with n1 = min(m, n), and n2 = n - n1.

The subroutine calls itself to factor ,

do the swaps on 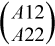, solve A12, update A22, then it calls itself to factor A22 and do the swaps on A21.

Input Parameters

m

INTEGER. The number of rows of the matrix A. m >= 0.

n

INTEGER. The number of columns of the matrix A. n >= 0.

a

REAL for sgetrf2

DOUBLE PRECISION for dgetrf2

COMPLEX for cgetrf2

DOUBLE COMPLEX for zgetrf2

Array, size (lda,n).

On entry, the m-by-n matrix to be factored.

lda

INTEGER. The leading dimension of the array a. lda >= max(1,m).

Output Parameters

On exit, the factors L and U from the factorization A = P * L * U; the unit diagonal elements of L are not stored.

ipiv

INTEGER. Array, size (min(m,n)).

The pivot indices; for 1 <= i <= min(m,n), row i of the matrix was interchanged with row ipiv(i).

info

INTEGER. = 0: successful exit.

< 0: if info = -i, the i-th argument had an illegal value.

> 0: if info = i, U_{i, i} is exactly zero. The factorization has been completed, but the factor U is exactly singular, and division by zero will occur if it is used to solve a system of equations.

Parent topic: Matrix Factorization: LAPACK Computational Routines

Select Your Language

Using Intel.com Search

Quick Links

Recent Searches

Advanced Search

Only search in

Developer Reference for Intel® oneAPI Math Kernel Library for Fortran

?getrf2