?lahef_rook

Developer Reference for Intel® oneAPI Math Kernel Library for Fortran

Download PDF

ID 766686

Date 3/31/2023

Version

Public

A newer version of this document is available. Customers should click here to go to the newest version.

Visible to Intel only — GUID: GUID-B8D3D016-A6B3-4D5E-A7F6-77D624F89A82

View Details

?lahef_rook

Computes a partial factorization of a complex Hermitian indefinite matrix, using the bounded Bunch-Kaufman diagonal pivoting method.

Syntax

call clahef_rook( uplo, n, nb, kb, a, lda, ipiv, w, ldw, info )

call zlahef_rook( uplo, n, nb, kb, a, lda, ipiv, w, ldw, info )

Include Files

mkl.fi

Description

The routine ?lahef_rook computes a partial factorization of a complex Hermitian matrix A, using the bounded Bunch-Kaufman ("rook") diagonal pivoting method. The partial factorization has the form:

If uplo = 'U':

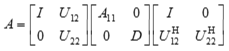
If uplo = 'L':

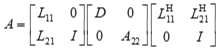
where the order of D is at most nb.

The actual order is returned in the argument kb, and is either nb or nb-1, or n if n ≤ nb.

Note that U^H denotes the conjugate transpose of U.

This is an auxiliary routine called by ?hetrf_rook. It uses blocked code (calling Level 3 BLAS) to update the submatrix A₁₁ (if uplo = 'U') or A₂₂ (if uplo = 'L').

Input Parameters

uplo

CHARACTER*1.

Specifies whether the upper or lower triangular part of the Hermitian matrix A is stored:

= 'U': upper triangular

= 'L': lower triangular

n

INTEGER. The order of the matrix A. n≥ 0.

nb

INTEGER. The maximum number of columns of the matrix A that should be factored. nb should be at least 2 to allow for 2-by-2 pivot blocks.

a

COMPLEX for clahef_rook

DOUBLE COMPLEX for zlahef_rook.

Array, DIMENSION (lda, n).

On entry, the Hermitian matrix A.

If uplo = 'U', the leading n-by-n upper triangular part of A contains the upper triangular part of the matrix A, and the strictly lower triangular part of A is not referenced.

If uplo = 'L', the leading n-by-n lower triangular part of A contains the lower triangular part of the matrix A, and the strictly upper triangular part of A is not referenced.

lda

INTEGER. The leading dimension of the array a. lda≥ max(1,n).

w

COMPLEX for clahef_rook

DOUBLE COMPLEX for zlahef_rook.

Workspace array, DIMENSION (ldw, nb).

ldw

INTEGER. The leading dimension of the array w. ldw≥ max(1,n).

Output Parameters

kb

INTEGER. The number of columns of A that were actually factored kb is either nb-1 or nb, or n if n ≤ nb.

a

On exit, A contains details of the partial factorization.

ipiv

INTEGER.

Array, DIMENSION (n ). Details of the interchanges and the block structure of D.

If uplo = 'U', only the last kb elements of ipiv are set;

if uplo = 'L', only the first kb elements are set.

If ipiv(k) > 0, then rows and columns k and ipiv(k) are interchanged and D(k, k) is a 1-by-1 diagonal block.

If uplo = 'U' and ipiv(k) < 0 and ipiv(k-1) < 0, then rows and columns k and -ipiv(k) are interchanged, rows and columns k - 1 and -ipiv(k - 1) are interchanged, and D_{k-1:k, k-1:k} is a 2-by-2 diagonal block.

If uplo = 'L' and ipiv(k) < 0 and ipiv(k + 1) < 0, then rows and columns k and -ipiv(k) are interchanged, rows and columns k + 1 and -ipiv(k + 1) are interchanged, and D_{k:k+1, k:k+1} is a 2-by-2 diagonal block.

info

INTEGER.

= 0: successful exit

> 0: if info = k, D(k, k) is exactly zero. The factorization has been completed, but the block diagonal matrix D is exactly singular.

Parent topic: LAPACK Auxiliary Routines

Select Your Language

Using Intel.com Search

Quick Links

Recent Searches

Advanced Search

Only search in

Developer Reference for Intel® oneAPI Math Kernel Library for Fortran

?lahef_rook