?laqtr

Developer Reference for Intel® oneAPI Math Kernel Library for Fortran

Download PDF

ID 766686

Date 3/31/2023

Version

Public

A newer version of this document is available. Customers should click here to go to the newest version.

Visible to Intel only — GUID: GUID-89F9A544-C9DB-43E5-96D0-F025BF8DC0B2

View Details

?laqtr

Solves a real quasi-triangular system of equations, or a complex quasi-triangular system of special form, in real arithmetic.

Syntax

call slaqtr( ltran, lreal, n, t, ldt, b, w, scale, x, work, info )

call dlaqtr( ltran, lreal, n, t, ldt, b, w, scale, x, work, info )

Include Files

mkl.fi

Description

The routine ?laqtr solves the real quasi-triangular system

op(T) * p = scale*c, if lreal = .TRUE.

or the complex quasi-triangular systems

op(T + iB)*(p+iq) = scale*(c+id), if lreal = .FALSE.

in real arithmetic, where T is upper quasi-triangular.

If lreal = .FALSE., then the first diagonal block of T must be 1-by-1, B is the specially structured matrix

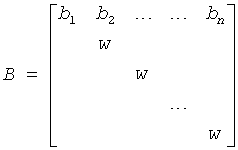
op(A) = A or A^T, A^T denotes the transpose of matrix A.

On input,

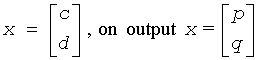
This routine is designed for the condition number estimation in routine ?trsna.

Input Parameters

ltran

LOGICAL.

On entry, ltran specifies the option of conjugate transpose:

= .FALSE., op(T + iB) = T + iB,

= .TRUE., op(T + iB) = (T + iB)^T.

lreal

LOGICAL.

On entry, lreal specifies the input matrix structure:

= .FALSE., the input is complex

= .TRUE., the input is real.

n

INTEGER.

On entry, n specifies the order of T + iB. n≥ 0.

t

REAL for slaqtr

DOUBLE PRECISION for dlaqtr

Array, dimension (ldt,n). On entry, t contains a matrix in Schur canonical form. If lreal = .FALSE., then the first diagonal block of t must be 1-by-1.

ldt

INTEGER. The leading dimension of the matrix T.

ldt≥ max(1,n).

b

REAL for slaqtr

DOUBLE PRECISION for dlaqtr

Array, dimension (n). On entry, b contains the elements to form the matrix B as described above. If lreal = .TRUE., b is not referenced.

w

REAL for slaqtr

DOUBLE PRECISION for dlaqtr

On entry, w is the diagonal element of the matrix B.

If lreal = .TRUE., w is not referenced.

x

REAL for slaqtr

DOUBLE PRECISION for dlaqtr

Array, dimension (2n). On entry, x contains the right hand side of the system.

work

REAL for slaqtr

DOUBLE PRECISION for dlaqtr

Workspace array, dimension (n).

Output Parameters

scale

REAL for slaqtr

DOUBLE PRECISION for dlaqtr

On exit, scale is the scale factor.

x

On exit, X is overwritten by the solution.

info

INTEGER.

If info = 0: successful exit.

If info = 1: the some diagonal 1-by-1 block has been perturbed by a small number smin to keep nonsingularity.

If info = 2: the some diagonal 2-by-2 block has been perturbed by a small number in ?laln2 to keep nonsingularity.

NOTE:

For higher speed, this routine does not check the inputs for errors.

Parent topic: LAPACK Auxiliary Routines

Select Your Language

Using Intel.com Search

Quick Links

Recent Searches

Advanced Search

Only search in

Developer Reference for Intel® oneAPI Math Kernel Library for Fortran

?laqtr