?getrs_batch

Developer Reference for Intel® oneAPI Math Kernel Library for Fortran

Download PDF

ID 766686

Date 3/31/2023

Version

Public

A newer version of this document is available. Customers should click here to go to the newest version.

Visible to Intel only — GUID: GUID-FE2A2926-DF94-47CB-B02D-C7099E283731

View Details

?getrs_batch_strided

Solves a group of systems of linear equations, each with an LU-factored square coefficient matrix and multiple right hand sides.

Syntax

call sgetrs_batch_strided(trans, n, nrhs, A, lda, stride_a, ipiv, stride_ipiv, b, ldb, stride_b, batch_size, info)

call dgetrs_batch_strided(trans, n, nrhs, A, lda, stride_a, ipiv, stride_ipiv, b, ldb, stride_b, batch_size, info)

call cgetrs_batch_strided(trans, n, nrhs, A, lda, stride_a, ipiv, stride_ipiv, b, ldb, stride_b, batch_size, info)

call zgetrs_batch_strided(trans, n, nrhs, A, lda, stride_a, ipiv, stride_ipiv, b, ldb, stride_b, batch_size, info)

Include Files

mkl.fi

Description

The ?getrs_batch_strided routines are similar to the ?getrs counterparts, but instead solve a group of systems of linear equations. Before calling this routine, you must call ?getrf_batch_strided to compute the LU factorization of the square coefficient matrix of each linear system.

All coefficient matrices, A_i have the same parameters (matrix size, leading dimension) and are stored at constant stride_a from each other. Similarly, all right-hand-side matrices, B_i, have the same parameters and are stored at constant stride_b from each other. The respective pivot array associated with each of the LU-factored A_i matrices are stored at constant stride_ipiv from each other. The operation is defined as

for i = 0 … batch_size-1
    A_i, B_i are matrices at offset i * stride_a, i * stride_b from A and B
    ipivi is an array at offset i * stride_ipiv from ipiv 
    Solve the system
	A_i * X_i = B_i  , if trans=’N’
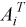	 * X_i = B_i  , if trans=’T’
	 * X_i = B_i , if trans=’C’ (for complex matrices)
end for

Input Parameters

trans

CHARACTER*1. Must be 'N', 'T', or 'C'.

Indicates the form of the systems of linear equations:

If trans = 'N', A_i * X_i = B_i is solved for X_i.

If trans = 'T', * X_i = B_i is solved for X_i.

If trans = 'C', * X_i = B_i is solved for X_i.

n

INTEGER. The order fo the A_i matrices; n ≥ 0.

nrhs

INTEGER. The number of right hand sides in each linear system of equations (nrhs ≥ 0).

A, B

REAL for sgetrs_batch_strided

DOUBLE PRECISION for dgetrs_batch_strided

COMPLEX for cgetrs_batch_strided

DOUBLE COMPLEX for zgetrs_batch_strided

The A array of size at least stride_a * batch_size holding the LU-factorized A_i matrices resulting from the call to ?getrf_batch_strided.

The B array of size at least stride_b * batch_size holding the B_i matrices, whose columns are the right -hand sides for each linear system of equations.

lda

INTEGER. Specifies the leading dimension of the A_i matrices; lda ≥ max(1,n).

ldb

INTEGER. Specifies the leading dimension of the B_i matrices; ldb ≥ max(1,n).

stride_a

INTEGER.

Stride between two consecutive A_i matrices; stride_a ≥ lda * n.

stride_b

INTEGER.

Stride between two consecutive B_i matrices; stride_b ≥ ldb * nrhs.

ipiv

INTEGER.

Array of size at least stride_ipiv * batch_size holding the pivoting indices for each LU-factorized matrix A_i.

stride_ipiv

INTEGER.

Stride between two consecutive pivot arrays; stride_ipiv ≥ n).

batch_size

INTEGER.

Number of linear systems to be solved; batch_size ≥ 0.

Output Parameters

B

Array is overwritten by the solution matrices X_i.

info

INTEGER.

Array of size at least batch_size, which reports the status for each linear system solve.

If info(i) = 0, the execution is successful for A_i.

If info(i) = -j, the j-th parameter had an illegal value for A_i.

Parent topic: Solving Systems of Linear Equations: LAPACK Computational Routines

Select Your Language

Using Intel.com Search

Quick Links

Recent Searches

Advanced Search

Only search in

Developer Reference for Intel® oneAPI Math Kernel Library for Fortran

?getrs_batch_strided