Developer Reference for Intel® oneAPI Math Kernel Library for C
A newer version of this document is available. Customers should click here to go to the newest version.
?ggrqf
Computes the generalized RQ factorization of two matrices.
Syntax
lapack_int LAPACKE_sggrqf (int matrix_layout, lapack_int m, lapack_int p, lapack_int n, float* a, lapack_int lda, float* taua, float* b, lapack_int ldb, float* taub);
lapack_int LAPACKE_dggrqf (int matrix_layout, lapack_int m, lapack_int p, lapack_int n, double* a, lapack_int lda, double* taua, double* b, lapack_int ldb, double* taub);
lapack_int LAPACKE_cggrqf (int matrix_layout, lapack_int m, lapack_int p, lapack_int n, lapack_complex_float* a, lapack_int lda, lapack_complex_float* taua, lapack_complex_float* b, lapack_int ldb, lapack_complex_float* taub);
lapack_int LAPACKE_zggrqf (int matrix_layout, lapack_int m, lapack_int p, lapack_int n, lapack_complex_double* a, lapack_int lda, lapack_complex_double* taua, lapack_complex_double* b, lapack_int ldb, lapack_complex_double* taub);
Include Files
- mkl.h
Description
The routine forms the generalized RQ factorization of an m-by-n matrix A and an p-by-n matrix B as A = R*Q, B = Z*T*Q, where Q is an n-by-n orthogonal/unitary matrix, Z is a p-by-p orthogonal/unitary matrix, and R and T assume one of the forms:
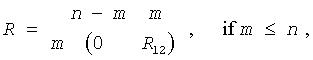
or
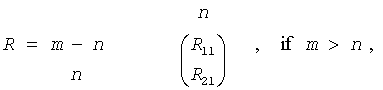
where R11 or R21 is upper triangular, and
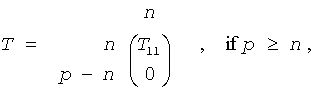
or
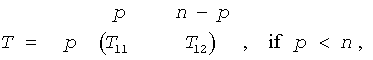
where T11 is upper triangular.
In particular, if B is square and nonsingular, the GRQ factorization of A and B implicitly gives the RQ factorization of A*B-1 as:
A*B-1 = (R*T-1)*ZT (for real flavors) or A*B-1 = (R*T-1)*ZH (for complex flavors).
Input Parameters
- matrix_layout
-
Specifies whether matrix storage layout is row major (LAPACK_ROW_MAJOR) or column major (LAPACK_COL_MAJOR).
- m
-
The number of rows of the matrix A (m≥ 0).
- p
-
The number of rows in B (p≥ 0).
- n
-
The number of columns of the matrices A and B (n≥ 0).
- a, b
-
Arrays:
a(size max(1, lda*n) for column major layout and max(1, lda*m) for row major layout) contains the m-by-n matrix A.
b(size max(1, ldb*n) for column major layout and max(1, ldb*p) for row major layout) contains the p-by-n matrix B.
- lda
-
The leading dimension of a; at least max(1, m)for column major layout and max(1, n) for row major layout.
- ldb
-
The leading dimension of b; at least max(1, p)for column major layout and max(1, n) for row major layout.
Output Parameters
- a, b
-
Overwritten by the factorization data as follows:
on exit, if m≤n, element Ri j (1<=i≤j≤m) of upper triangular matrix R is stored in a[(i - 1) + (n - m + j - 1)*lda] for column major layout and in a[(i - 1)*lda + (n - m + j - 1)] for row major layout.
if m > n, the elements on and above the (m-n)th subdiagonal contain the m-by-n upper trapezoidal matrix R;
the remaining elements, with the array taua, represent the orthogonal/unitary matrix Q as a product of elementary reflectors.
The elements on and above the diagonal of the array b contain the min(p,n)-by-n upper trapezoidal matrix T (T is upper triangular if p≥n); the elements below the diagonal, with the array taub, represent the orthogonal/unitary matrix Z as a product of elementary reflectors.
- taua, taub
-
Arrays, size at least max (1, min(m, n)) for taua and at least max (1, min(p, n)) for taub.
The array taua contains the scalar factors of the elementary reflectors which represent the orthogonal/unitary matrix Q.
The array taub contains the scalar factors of the elementary reflectors which represent the orthogonal/unitary matrix Z.
Return Values
This function returns a value info.
If info=0, the execution is successful.
If info = -i, the i-th parameter had an illegal value.
Application Notes
The matrix Q is represented as a product of elementary reflectors
Q = H(1)H(2)...H(k), where k = min(m,n).
Each H(i) has the form
H(i) = I - taua*v*vT for real flavors, or
H(i) = I - taua*v*vH for complex flavors,
where taua is a real/complex scalar, and v is a real/complex vector with vn - k + i = 1, vn - k + i + 1:n = 0.
On exit, v1:n - k + i - 1 is stored in a(m-k+i,1:n-k+i-1) and taua is stored in taua[i - 1].
The matrix Z is represented as a product of elementary reflectors
Z = H(1)H(2)...H(k), where k = min(p,n).
Each H(i) has the form
H(i) = I - taub*v*vT for real flavors, or
H(i) = I - taub*v*vH for complex flavors,
where taub is a real/complex scalar, and v is a real/complex vector with v1:i - 1 = 0, vi = 1.
On exit, vi + 1:p is stored in b(i+1:p, i) and taub is stored in taub[i - 1].