?gees

Developer Reference for Intel® oneAPI Math Kernel Library for C

Download PDF

ID 766684

Date 11/07/2023

Version

Public

A newer version of this document is available. Customers should click here to go to the newest version.

Visible to Intel only — GUID: GUID-62CD3B14-6590-4162-BD5C-4EAB5A6DCD50

View Details

?gees

Computes the eigenvalues and Schur factorization of a general matrix, and orders the factorization so that selected eigenvalues are at the top left of the Schur form.

Syntax

lapack_int LAPACKE_sgees( int matrix_layout, char jobvs, char sort, LAPACK_S_SELECT2 select, lapack_int n, float* a, lapack_int lda, lapack_int* sdim, float* wr, float* wi, float* vs, lapack_int ldvs );

lapack_int LAPACKE_dgees( int matrix_layout, char jobvs, char sort, LAPACK_D_SELECT2 select, lapack_int n, double* a, lapack_int lda, lapack_int* sdim, double* wr, double* wi, double* vs, lapack_int ldvs );

lapack_int LAPACKE_cgees( int matrix_layout, char jobvs, char sort, LAPACK_C_SELECT1 select, lapack_int n, lapack_complex_float* a, lapack_int lda, lapack_int* sdim, lapack_complex_float* w, lapack_complex_float* vs, lapack_int ldvs );

lapack_int LAPACKE_zgees( int matrix_layout, char jobvs, char sort, LAPACK_Z_SELECT1 select, lapack_int n, lapack_complex_double* a, lapack_int lda, lapack_int* sdim, lapack_complex_double* w, lapack_complex_double* vs, lapack_int ldvs );

Include Files

mkl.h

Description

The routine computes for an n-by-n real/complex nonsymmetric matrix A, the eigenvalues, the real Schur form T, and, optionally, the matrix of Schur vectors Z. This gives the Schur factorization A = Z*T*Z^H.

Optionally, it also orders the eigenvalues on the diagonal of the real-Schur/Schur form so that selected eigenvalues are at the top left. The leading columns of Z then form an orthonormal basis for the invariant subspace corresponding to the selected eigenvalues.

A real matrix is in real-Schur form if it is upper quasi-triangular with 1-by-1 and 2-by-2 blocks. 2-by-2 blocks will be standardized in the form

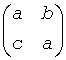
where b*c < 0. The eigenvalues of such a block are 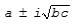Equation

A complex matrix is in Schur form if it is upper triangular.

Input Parameters

matrix_layout

Specifies whether matrix storage layout is row major (LAPACK_ROW_MAJOR) or column major (LAPACK_COL_MAJOR).

jobvs

Must be 'N' or 'V'.

If jobvs = 'N', then Schur vectors are not computed.

If jobvs = 'V', then Schur vectors are computed.

sort

Must be 'N' or 'S'. Specifies whether or not to order the eigenvalues on the diagonal of the Schur form.

If sort = 'N', then eigenvalues are not ordered.

If sort = 'S', eigenvalues are ordered (see select).

select

If sort = 'S', select is used to select eigenvalues to sort to the top left of the Schur form.

If sort = 'N', select is not referenced.

For real flavors:

An eigenvalue wr[j]+sqrt(-1)*wi[j] is selected if select(wr[j], wi[j]) is true; that is, if either one of a complex conjugate pair of eigenvalues is selected, then both complex eigenvalues are selected.

For complex flavors:

An eigenvalue w[j] is selected if select(w[j]) is true.

Note that a selected complex eigenvalue may no longer satisfy select(wr[j], wi[j])= 1 after ordering, since ordering may change the value of complex eigenvalues (especially if the eigenvalue is ill-conditioned); in this case info may be set to n+2 (see info below).

n

The order of the matrix A (n≥ 0).

a

Arrays:

a (size at least max(1, lda*n)) is an array containing the n-by-n matrix A.

lda

The leading dimension of the array a. Must be at least max(1, n).

ldvs

The leading dimension of the output array vs. Constraints:

ldvs≥ 1;

ldvs≥ max(1, n) if jobvs = 'V'.

Output Parameters

a

On exit, this array is overwritten by the real-Schur/Schur form T.

sdim

If sort = 'N', sdim= 0.

If sort = 'S', sdim is equal to the number of eigenvalues (after sorting) for which select is true.

Note that for real flavors complex conjugate pairs for which select is true for either eigenvalue count as 2.

wr, wi

Arrays, size at least max (1, n) each. Contain the real and imaginary parts, respectively, of the computed eigenvalues, in the same order that they appear on the diagonal of the output real-Schur form T. Complex conjugate pairs of eigenvalues appear consecutively with the eigenvalue having positive imaginary part first.

w

Array, size at least max(1, n). Contains the computed eigenvalues. The eigenvalues are stored in the same order as they appear on the diagonal of the output Schur form T.

vs

Array vs (size at least max(1, ldvs*n)) .

If jobvs = 'V', vs contains the orthogonal/unitary matrix Z of Schur vectors.

If jobvs = 'N', vs is not referenced.

Return Values

This function returns a value info.

If info=0, the execution is successful.

If info = -i, the i-th parameter had an illegal value.

If info = i, and

i≤n:

the QR algorithm failed to compute all the eigenvalues; elements 1:ilo-1 and i+1:n of wr and wi (for real flavors) or w (for complex flavors) contain those eigenvalues which have converged; if jobvs = 'V', vs contains the matrix which reduces A to its partially converged Schur form;

i = n+1:

the eigenvalues could not be reordered because some eigenvalues were too close to separate (the problem is very ill-conditioned);

i = n+2:

after reordering, round-off changed values of some complex eigenvalues so that leading eigenvalues in the Schur form no longer satisfy select = 1. This could also be caused by underflow due to scaling.

Parent topic: Nonsymmetric Eigenvalue Problems: LAPACK Driver Routines

Select Your Language

Using Intel.com Search

Quick Links

Recent Searches

Advanced Search

Only search in

Developer Reference for Intel® oneAPI Math Kernel Library for C

?gees

Syntax

Include Files

Description

Input Parameters

Output Parameters

Return Values