?poequ

Developer Reference for Intel® oneAPI Math Kernel Library for C

Download PDF

ID 766684

Date 7/13/2023

Version

Public

A newer version of this document is available. Customers should click here to go to the newest version.

Visible to Intel only — GUID: GUID-61BD0B69-59E9-4946-9CAD-A20D6D5E84E2

View Details

?poequ

Computes row and column scaling factors intended to equilibrate a symmetric (Hermitian) positive definite matrix and reduce its condition number.

Syntax

lapack_int LAPACKE_spoequ( int matrix_layout, lapack_int n, const float* a, lapack_int lda, float* s, float* scond, float* amax );

lapack_int LAPACKE_dpoequ( int matrix_layout, lapack_int n, const double* a, lapack_int lda, double* s, double* scond, double* amax );

lapack_int LAPACKE_cpoequ( int matrix_layout, lapack_int n, const lapack_complex_float* a, lapack_int lda, float* s, float* scond, float* amax );

lapack_int LAPACKE_zpoequ( int matrix_layout, lapack_int n, const lapack_complex_double* a, lapack_int lda, double* s, double* scond, double* amax );

Include Files

mkl.h

Description

The routine computes row and column scalings intended to equilibrate a symmetric (Hermitian) positive-definite matrix A and reduce its condition number (with respect to the two-norm). The output array s returns scale factors such that contains

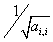
These factors are chosen so that the scaled matrix B with elements B_i,j=s[i-1]*A_i,j*s[j-1] has diagonal elements equal to 1.

This choice of s puts the condition number of B within a factor n of the smallest possible condition number over all possible diagonal scalings.

Input Parameters

matrix_layout	Specifies whether matrix storage layout is row major (LAPACK_ROW_MAJOR) or column major (LAPACK_COL_MAJOR).
n	The order of the matrix `A`; `n≥ 0`.
a	Array: size max(1, lda*n) . Contains the `n`-by-`n` symmetric or Hermitian positive definite matrix `A` whose scaling factors are to be computed. Only the diagonal elements of `A` are referenced.
lda	The leading dimension of `a`; `lda≥ max(1,n)`.

Output Parameters

Array, size n.

If info = 0, the array s contains the scale factors for A.

scond

If info = 0, scond contains the ratio of the smallest s[i] to the largest s[i].

amax

Absolute value of the largest element of the matrix A.

Return Values

This function returns a value info.

If info = 0, the execution is successful.

If info = -i, parameter i had an illegal value.

If info = i, the i-th diagonal element of A is nonpositive.

Application Notes

If scond≥ 0.1 and amax is neither too large nor too small, it is not worth scaling by s.

If amax is very close to SMLNUM or very close to BIGNUM, the matrix A should be scaled.

Parent topic: Matrix Equilibration: LAPACK Computational Routines

Select Your Language

Using Intel.com Search

Quick Links

Recent Searches

Advanced Search

Only search in

Developer Reference for Intel® oneAPI Math Kernel Library for C

?poequ

Syntax

Include Files

Description

Input Parameters

Output Parameters

Return Values

Application Notes

See Also