?hseqr

Developer Reference for Intel® oneAPI Math Kernel Library for C

Download PDF

ID 766684

Date 7/13/2023

Version

Public

A newer version of this document is available. Customers should click here to go to the newest version.

Visible to Intel only — GUID: GUID-3F910967-04C1-4C67-8467-F431B2CD8E1C

View Details

?hseqr

Computes all eigenvalues and (optionally) the Schur factorization of a matrix reduced to Hessenberg form.

Syntax

lapack_int LAPACKE_shseqr( int matrix_layout, char job, char compz, lapack_int n, lapack_int ilo, lapack_int ihi, float* h, lapack_int ldh, float* wr, float* wi, float* z, lapack_int ldz );

lapack_int LAPACKE_dhseqr( int matrix_layout, char job, char compz, lapack_int n, lapack_int ilo, lapack_int ihi, double* h, lapack_int ldh, double* wr, double* wi, double* z, lapack_int ldz );

lapack_int LAPACKE_chseqr( int matrix_layout, char job, char compz, lapack_int n, lapack_int ilo, lapack_int ihi, lapack_complex_float* h, lapack_int ldh, lapack_complex_float* w, lapack_complex_float* z, lapack_int ldz );

lapack_int LAPACKE_zhseqr( int matrix_layout, char job, char compz, lapack_int n, lapack_int ilo, lapack_int ihi, lapack_complex_double* h, lapack_int ldh, lapack_complex_double* w, lapack_complex_double* z, lapack_int ldz );

Include Files

mkl.h

Description

The routine computes all the eigenvalues, and optionally the Schur factorization, of an upper Hessenberg matrix H: H = Z*T*Z^H, where T is an upper triangular (or, for real flavors, quasi-triangular) matrix (the Schur form of H), and Z is the unitary or orthogonal matrix whose columns are the Schur vectors z_i.

You can also use this routine to compute the Schur factorization of a general matrix A which has been reduced to upper Hessenberg form H:

A = Q*H*Q^H, where Q is unitary (orthogonal for real flavors);

A = (QZ)*T*(QZ)^H.

In this case, after reducing A to Hessenberg form by gehrd, call orghr to form Q explicitly and then pass Q to ?hseqr with compz = 'V'.

You can also call gebal to balance the original matrix before reducing it to Hessenberg form by ?hseqr, so that the Hessenberg matrix H will have the structure:

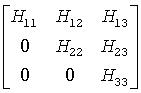
where H₁₁ and H₃₃ are upper triangular.

If so, only the central diagonal block H₂₂ (in rows and columns ilo to ihi) needs to be further reduced to Schur form (the blocks H₁₂ and H₂₃ are also affected). Therefore the values of ilo and ihi can be supplied to ?hseqr directly. Also, after calling this routine you must call gebak to permute the Schur vectors of the balanced matrix to those of the original matrix.

If ?gebal has not been called, however, then ilo must be set to 1 and ihi to n. Note that if the Schur factorization of A is required, ?gebal must not be called with job = 'S' or 'B', because the balancing transformation is not unitary (for real flavors, it is not orthogonal).

?hseqr uses a multishift form of the upper Hessenberg QR algorithm. The Schur vectors are normalized so that ||z_i||₂ = 1, but are determined only to within a complex factor of absolute value 1 (for the real flavors, to within a factor ±1).

Input Parameters

job

Must be 'E' or 'S'.

If job = 'E', then eigenvalues only are required.

If job = 'S', then the Schur form T is required.

compz

Must be 'N' or 'I' or 'V'.

If compz = 'N', then no Schur vectors are computed (and the array z is not referenced).

If compz = 'I', then the Schur vectors of H are computed (and the array z is initialized by the routine).

If compz = 'V', then the Schur vectors of A are computed (and the array z must contain the matrix Q on entry).

n

The order of the matrix H (n≥ 0).

ilo, ihi

If A has been balanced by ?gebal, then ilo and ihi must contain the values returned by ?gebal. Otherwise, ilo must be set to 1 and ihi to n.

h, z

Arrays:

h (size max(1, ldh*n)) ) The n-by-n upper Hessenberg matrix H.

z (size max(1, ldz*n))

If compz = 'V', then z must contain the matrix Q from the reduction to Hessenberg form.

If compz = 'I', then z need not be set.

If compz = 'N', then z is not referenced.

ldh

The leading dimension of h; at least max(1, n).

ldz

The leading dimension of z;

If compz = 'N', then ldz≥ 1.

If compz = 'V' or 'I', then ldz≥ max(1, n).

Output Parameters

w

Array, size at least max (1, n). Contains the computed eigenvalues, unless info>0. The eigenvalues are stored in the same order as on the diagonal of the Schur form T (if computed).

wr, wi

Arrays, size at least max (1, n) each.

Contain the real and imaginary parts, respectively, of the computed eigenvalues, unless info > 0. Complex conjugate pairs of eigenvalues appear consecutively with the eigenvalue having positive imaginary part first. The eigenvalues are stored in the same order as on the diagonal of the Schur form T (if computed).

h

If info = 0 and job = 'S', h contains the upper quasi-triangular matrix T from the Schur decomposition (the Schur form).

If info = 0 and job = 'E', the contents of h are unspecified on exit. (The output value of h when info > 0 is given under the description of info below.)

z

If compz = 'V' and info = 0, then z contains Q*Z.

If compz = 'I' and info = 0, then z contains the unitary or orthogonal matrix Z of the Schur vectors of H.

If compz = 'N', then z is not referenced.

Return Values

This function returns a value info.

If info = 0, the execution is successful.

If info = -i, the i-th parameter had an illegal value.

If info = i, ?hseqr failed to compute all of the eigenvalues. Elements 1,2, ..., ilo-1 and i+1, i+2, ..., n of the eigenvalue arrays (wr and wi for real flavors and w for complex flavors) contain the real and imaginary parts of those eigenvalues that have been successfully found.

If info > 0, and job = 'E', then on exit, the remaining unconverged eigenvalues are the eigenvalues of the upper Hessenberg matrix rows and columns ilo through info of the final output value of H.

If info > 0, and job = 'S', then on exit (initial value of H)*U = U*(final value of H), where U is a unitary matrix. The final value of H is upper Hessenberg and triangular in rows and columns info+1 through ihi.

If info > 0, and compz = 'V', then on exit (final value of Z) = (initial value of Z)*U, where U is the unitary matrix (regardless of the value of job).

If info > 0, and compz = 'I', then on exit (final value of Z) = U, where U is the unitary matrix (regardless of the value of job).

If info > 0, and compz = 'N', then Z is not accessed.

Application Notes

The computed Schur factorization is the exact factorization of a nearby matrix H + E, where ||E||₂ < O(ε) ||H||₂/s_i, and ε is the machine precision.

If λ_i is an exact eigenvalue, and μ_i is the corresponding computed value, then |λ_i - μ_i|≤c(n)*ε*||H||₂/s_i, where c(n) is a modestly increasing function of n, and s_i is the reciprocal condition number of λ_i. The condition numbers s_i may be computed by calling trsna.

The total number of floating-point operations depends on how rapidly the algorithm converges; typical numbers are as follows.

If only eigenvalues are computed:

7n³ for real flavors

25n³ for complex flavors.

If the Schur form is computed:

10n³ for real flavors

35n³ for complex flavors.

If the full Schur factorization is computed:

20n³ for real flavors

70n³ for complex flavors.

Parent topic: Nonsymmetric Eigenvalue Problems: LAPACK Computational Routines

Select Your Language

Using Intel.com Search

Quick Links

Recent Searches

Advanced Search

Only search in

Developer Reference for Intel® oneAPI Math Kernel Library for C

?hseqr

Syntax

Include Files

Description

Input Parameters

Output Parameters

Return Values

Application Notes