Developer Reference for Intel® oneAPI Math Kernel Library for C
A newer version of this document is available. Customers should click here to go to the newest version.
?tgsja
Computes the generalized SVD of two upper triangular or trapezoidal matrices.
Syntax
lapack_int LAPACKE_stgsja( int matrix_layout, char jobu, char jobv, char jobq, lapack_int m, lapack_int p, lapack_int n, lapack_int k, lapack_int l, float* a, lapack_int lda, float* b, lapack_int ldb, float tola, float tolb, float* alpha, float* beta, float* u, lapack_int ldu, float* v, lapack_int ldv, float* q, lapack_int ldq, lapack_int* ncycle );
lapack_int LAPACKE_dtgsja( int matrix_layout, char jobu, char jobv, char jobq, lapack_int m, lapack_int p, lapack_int n, lapack_int k, lapack_int l, double* a, lapack_int lda, double* b, lapack_int ldb, double tola, double tolb, double* alpha, double* beta, double* u, lapack_int ldu, double* v, lapack_int ldv, double* q, lapack_int ldq, lapack_int* ncycle );
lapack_int LAPACKE_ctgsja( int matrix_layout, char jobu, char jobv, char jobq, lapack_int m, lapack_int p, lapack_int n, lapack_int k, lapack_int l, lapack_complex_float* a, lapack_int lda, lapack_complex_float* b, lapack_int ldb, float tola, float tolb, float* alpha, float* beta, lapack_complex_float* u, lapack_int ldu, lapack_complex_float* v, lapack_int ldv, lapack_complex_float* q, lapack_int ldq, lapack_int* ncycle );
lapack_int LAPACKE_ztgsja( int matrix_layout, char jobu, char jobv, char jobq, lapack_int m, lapack_int p, lapack_int n, lapack_int k, lapack_int l, lapack_complex_double* a, lapack_int lda, lapack_complex_double* b, lapack_int ldb, double tola, double tolb, double* alpha, double* beta, lapack_complex_double* u, lapack_int ldu, lapack_complex_double* v, lapack_int ldv, lapack_complex_double* q, lapack_int ldq, lapack_int* ncycle );
Include Files
- mkl.h
Description
The routine computes the generalized singular value decomposition (GSVD) of two real/complex upper triangular (or trapezoidal) matrices A and B. On entry, it is assumed that matrices A and B have the following forms, which may be obtained by the preprocessing subroutine ggsvp from a general m-by-n matrix A and p-by-n matrix B:
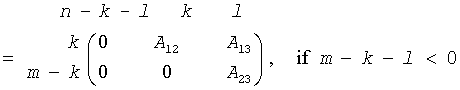
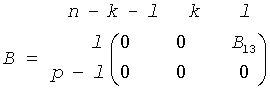
where the k-by-k matrix A12 and l-by-l matrix B13 are nonsingular upper triangular; A23 is l-by-l upper triangular if m-k-l≥0, otherwise A23 is (m-k)-by-l upper trapezoidal.
On exit,
UH*A*Q = D1*(0 R), VH*B*Q = D2*(0 R),
where U, V and Q are orthogonal/unitary matrices, R is a nonsingular upper triangular matrix, and D1 and D2 are "diagonal" matrices, which are of the following structures:
If m-k-l≥0,
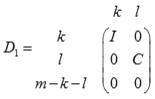
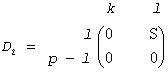
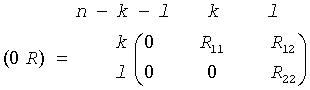
where
C = diag(alpha[k],...,alpha[k+l-1])
S = diag(beta[k],...,beta[k+l-1])
C2 + S2 = I
R is stored in a(1:k+l, n-k-l+1:n ) on exit.
If m-k-l < 0,
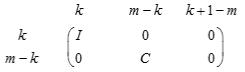
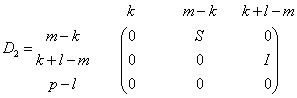
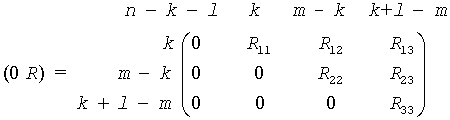
where
C = diag(alpha[k],...,alpha[m-1]),
S = diag(beta[k],...,beta[m-1]),
C2 + S2 = I
On exit,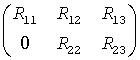 
is stored in a(1:m, n-k-l+1:n ) and R33 is stored
in b(m-k+1:l, n+m-k-l+1:n ).
The computation of the orthogonal/unitary transformation matrices U, V or Q is optional. These matrices may either be formed explicitly, or they may be postmultiplied into input matrices U1, V1, or Q1.
Input Parameters
- matrix_layout
-
Specifies whether matrix storage layout is row major (LAPACK_ROW_MAJOR) or column major (LAPACK_COL_MAJOR).
- jobu
-
Must be 'U', 'I', or 'N'.
If jobu = 'U', u must contain an orthogonal/unitary matrix U1 on entry.
If jobu = 'I', u is initialized to the unit matrix.
If jobu = 'N', u is not computed.
- jobv
-
Must be 'V', 'I', or 'N'.
If jobv = 'V', v must contain an orthogonal/unitary matrix V1 on entry.
If jobv = 'I', v is initialized to the unit matrix.
If jobv = 'N', v is not computed.
- jobq
-
Must be 'Q', 'I', or 'N'.
If jobq = 'Q', q must contain an orthogonal/unitary matrix Q1 on entry.
If jobq = 'I', q is initialized to the unit matrix.
If jobq = 'N', q is not computed.
- m
-
The number of rows of the matrix A (m≥ 0).
- p
-
The number of rows of the matrix B (p≥ 0).
- n
-
The number of columns of the matrices A and B (n≥ 0).
- k, l
-
Specify the subblocks in the input matrices A and B, whose GSVD is computed.
- a, b, u, v, q
-
Arrays:
a(size at least max(1, lda*n) for column major layout and max(1, lda*m) for row major layout) contains the m-by-n matrix A.
b(size at least max(1, ldb*n) for column major layout and max(1, ldb*p) for row major layout) contains the p-by-n matrix B.
If jobu = 'U', u (size max(1, ldu*m)) must contain a matrix U1 (usually the orthogonal/unitary matrix returned by ?ggsvp).
If jobv = 'V', v (size at least max(1, ldv*p)) must contain a matrix V1 (usually the orthogonal/unitary matrix returned by ?ggsvp).
If jobq = 'Q', q (size at least max(1, ldq*n)) must contain a matrix Q1 (usually the orthogonal/unitary matrix returned by ?ggsvp).
- lda
-
The leading dimension of a; at least max(1, m)for column major layout and max(1, n) for row major layout.
- ldb
-
The leading dimension of b; at least max(1, p) for column major layout and max(1, n) for row major layout.
- ldu
-
The leading dimension of the array u .
ldu≥ max(1, m) if jobu = 'U'; ldu≥ 1 otherwise.
- ldv
-
The leading dimension of the array v .
ldv≥ max(1, p) if jobv = 'V'; ldv≥ 1 otherwise.
- ldq
-
The leading dimension of the array q .
ldq≥ max(1, n) if jobq = 'Q'; ldq≥ 1 otherwise.
- tola, tolb
-
tola and tolb are the convergence criteria for the Jacobi-Kogbetliantz iteration procedure. Generally, they are the same as used in ?ggsvp:
tola = max(m, n)*|A|*MACHEPS,
tolb = max(p, n)*|B|*MACHEPS.
Output Parameters
- a
-
On exit, a(n-k+1:n, 1:min(k+l, m)) contains the triangular matrix R or part of R.
- b
-
On exit, if necessary, b(m-k+1: l, n+m-k-l+1: n)) contains a part of R.
- alpha, beta
-
Arrays, size at least max(1, n). Contain the generalized singular value pairs of A and B:
alpha(1:k) = 1,
beta(1:k) = 0,
and if m-k-l≥ 0,
alpha(k+1:k+l) = diag(C),
beta(k+1:k+l) = diag(S),
or if m-k-l < 0,
alpha(k+1:m)= diag(C), alpha(m+1:k+l)=0
beta(k+1:m) = diag(S),
beta(m+1:k+l) = 1.
Furthermore, if k+l < n,
alpha(k+l+1:n)= 0 and
beta(k+l+1:n) = 0.
- u
-
If jobu = 'I', u contains the orthogonal/unitary matrix U.
If jobu = 'U', u contains the product U1*U.
If jobu = 'N', u is not referenced.
- v
-
If jobv = 'I', v contains the orthogonal/unitary matrix U.
If jobv = 'V', v contains the product V1*V.
If jobv = 'N', v is not referenced.
- q
-
If jobq = 'I', q contains the orthogonal/unitary matrix U.
If jobq = 'Q', q contains the product Q1*Q.
If jobq = 'N', q is not referenced.
- ncycle
-
The number of cycles required for convergence.
Return Values
This function returns a value info.
If info=0, the execution is successful.
If info = -i, the i-th parameter had an illegal value.
If info = 1, the procedure does not converge after MAXIT cycles.