Developer Reference for Intel® oneAPI Math Kernel Library for Fortran

Download PDF
ID 766686
Date 7/13/2023
Public

A newer version of this document is available. Customers should click here to go to the newest version.

Document Table of Contents
Document Table of Contents x
Developer Reference for Intel® oneAPI Math Kernel Library - Fortran
Developer Reference for Intel® oneAPI Math Kernel Library - Fortran x
Getting Help and Support What's New Notational Conventions Overview OpenMP* Offload BLAS and Sparse BLAS Routines LAPACK Routines ScaLAPACK Routines Sparse Solver Routines Extended Eigensolver Routines Vector Mathematical Functions Statistical Functions Fourier Transform Functions PBLAS Routines Partial Differential Equations Support Nonlinear Optimization Problem Solvers Support Functions BLACS Routines Data Fitting Functions Appendix A: Linear Solvers Basics Appendix B: Routine and Function Arguments Appendix C: Specific Features of Fortran 95 Interfaces for LAPACK Routines Appendix D: FFTW Interface to Intel® Math Kernel Library Appendix E: Code Examples Appendix F: oneMKL Functionality Bibliography Glossary Notices and Disclaimers
Overview x
Performance Enhancements Parallelism
OpenMP* Offload x
OpenMP* Offload for Intel® oneAPI Math Kernel Library
BLAS and Sparse BLAS Routines x
BLAS Routines Sparse BLAS Level 1 Routines Sparse BLAS Level 2 and Level 3 Routines Sparse QR Routines Inspector-executor Sparse BLAS Routines BLAS-like Extensions
BLAS Routines x
Naming Conventions for BLAS Routines Fortran 95 Interface Conventions for BLAS Routines Matrix Storage Schemes for BLAS Routines BLAS Level 1 Routines and Functions BLAS Level 2 Routines BLAS Level 3 Routines
BLAS Level 1 Routines and Functions x
?asum ?axpy ?copy ?copy_batch ?copy_batch_strided ?dot ?sdot ?dotc ?dotu ?nrm2 ?rot ?rotg ?rotm ?rotmg ?scal ?swap i?amax i?amin ?cabs1
BLAS Level 2 Routines x
?gbmv ?gemv ?ger ?gerc ?geru ?hbmv ?hemv ?her ?her2 ?hpmv ?hpr ?hpr2 ?sbmv ?spmv ?spr ?spr2 ?symv ?syr ?syr2 ?tbmv ?tbsv ?tpmv ?tpsv ?trmv ?trsv
BLAS Level 3 Routines x
?gemm ?hemm ?herk ?her2k ?symm ?syrk ?syr2k ?trmm ?trsm
Sparse BLAS Level 1 Routines x
Vector Arguments Naming Conventions for Sparse BLAS Routines Routines and Data Types BLAS Level 1 Routines That Can Work With Sparse Vectors ?axpyi ?doti ?dotci ?dotui ?gthr ?gthrz ?roti ?sctr
Sparse BLAS Level 2 and Level 3 Routines x
Naming Conventions in Sparse BLAS Level 2 and Level 3 Sparse Matrix Storage Formats for Sparse BLAS Routines Routines and Supported Operations Interface Consideration Sparse BLAS Level 2 and Level 3 Routines.
Sparse BLAS Level 2 and Level 3 Routines. x
mkl_?csrgemv mkl_?bsrgemv mkl_?coogemv mkl_?diagemv mkl_?csrsymv mkl_?bsrsymv mkl_?coosymv mkl_?diasymv mkl_?csrtrsv mkl_?bsrtrsv mkl_?cootrsv mkl_?diatrsv mkl_cspblas_?csrgemv mkl_cspblas_?bsrgemv mkl_cspblas_?coogemv mkl_cspblas_?csrsymv mkl_cspblas_?bsrsymv mkl_cspblas_?coosymv mkl_cspblas_?csrtrsv mkl_cspblas_?bsrtrsv mkl_cspblas_?cootrsv mkl_?csrmv mkl_?bsrmv mkl_?cscmv mkl_?coomv mkl_?csrsv mkl_?bsrsv mkl_?cscsv mkl_?coosv mkl_?csrmm mkl_?bsrmm mkl_?cscmm mkl_?coomm mkl_?csrsm mkl_?cscsm mkl_?coosm mkl_?bsrsm mkl_?diamv mkl_?skymv mkl_?diasv mkl_?skysv mkl_?diamm mkl_?skymm mkl_?diasm mkl_?skysm mkl_?dnscsr mkl_?csrcoo mkl_?csrbsr mkl_?csrcsc mkl_?csrdia mkl_?csrsky mkl_?csradd mkl_?csrmultcsr mkl_?csrmultd
Sparse QR Routines x
mkl_sparse_set_qr_hint mkl_sparse_?_qr mkl_sparse_qr_reorder mkl_sparse_?_qr_factorize mkl_sparse_?_qr_solve mkl_sparse_?_qr_qmult mkl_sparse_?_qr_rsolve
Inspector-executor Sparse BLAS Routines x
Naming Conventions in Inspector-Executor Sparse BLAS Routines Sparse Matrix Storage Formats for Inspector-executor Sparse BLAS Routines Supported Inspector-executor Sparse BLAS Operations Two-stage Algorithm in Inspector-Executor Sparse BLAS Routines Matrix Manipulation Routines Inspector-Executor Sparse BLAS Analysis Routines Inspector-Executor Sparse BLAS Execution Routines
Matrix Manipulation Routines x
mkl_sparse_?_create_csr mkl_sparse_?_create_csc mkl_sparse_?_create_coo mkl_sparse_?_create_bsr mkl_sparse_copy mkl_sparse_destroy mkl_sparse_convert_csr mkl_sparse_convert_bsr mkl_sparse_?_export_csr mkl_sparse_?_export_csc mkl_sparse_?_export_bsr mkl_sparse_?_set_value mkl_sparse_?_update_values mkl_sparse_order
Inspector-Executor Sparse BLAS Analysis Routines x
mkl_sparse_set_lu_smoother_hint mkl_sparse_set_mv_hint mkl_sparse_set_sv_hint mkl_sparse_set_mm_hint mkl_sparse_set_sm_hint mkl_sparse_set_dotmv_hint mkl_sparse_set_symgs_hint mkl_sparse_set_sorv_hint mkl_sparse_set_memory_hint mkl_sparse_optimize
Inspector-Executor Sparse BLAS Execution Routines x
mkl_sparse_?_lu_smoother mkl_sparse_?_mv mkl_sparse_?_trsv mkl_sparse_?_mm mkl_sparse_?_trsm mkl_sparse_?_add mkl_sparse_spmm mkl_sparse_?_spmmd mkl_sparse_sp2m mkl_sparse_?_sp2md mkl_sparse_sypr mkl_sparse_?_syprd mkl_sparse_?_symgs mkl_sparse_?_symgs_mv mkl_sparse_syrk mkl_sparse_?_syrkd mkl_sparse_?_dotmv mkl_sparse_?_sorv
BLAS-like Extensions x
?axpy_batch ?axpy_batch_strided ?axpby ?gem2vu ?gem2vc ?gemmt ?gemm3m ?gemm_batch ?gemm_batch_strided ?gemm3m_batch ?trsm_batch ?trsm_batch_strided mkl_?imatcopy mkl_?imatcopy_batch mkl_?imatcopy_batch_strided mkl_?omatadd_batch_strided mkl_?omatcopy mkl_?omatcopy_batch mkl_?omatcopy_batch_strided mkl_?omatcopy2 mkl_?omatadd ?gemm_pack_get_size, gemm_*_pack_get_size ?gemm_pack gemm_*_pack ?gemm_compute gemm_*_compute ?gemm_free gemm_* ?gemv_batch_strided ?gemv_batch ?dgmm_batch_strided ?dgmm_batch mkl_jit_create_?gemm mkl_jit_get_?gemm_ptr mkl_jit_destroy
LAPACK Routines x
Naming Conventions for LAPACK Routines Fortran 95 Interface Conventions for LAPACK Routines Matrix Storage Schemes for LAPACK Routines Mathematical Notation for LAPACK Routines Error Analysis LAPACK Linear Equation Routines LAPACK Least Squares and Eigenvalue Problem Routines LAPACK Auxiliary Routines LAPACK Utility Functions and Routines LAPACK Test Functions and Routines Additional LAPACK Routines (Included for Compatibility with Netlib LAPACK)
Fortran 95 Interface Conventions for LAPACK Routines x
Intel® MKL Fortran 95 Interfaces for LAPACK Routines vs. Netlib Implementation
LAPACK Linear Equation Routines x
LAPACK Linear Equation Computational Routines LAPACK Linear Equation Driver Routines
LAPACK Linear Equation Computational Routines x
Matrix Factorization: LAPACK Computational Routines Solving Systems of Linear Equations: LAPACK Computational Routines Estimating the Condition Number: LAPACK Computational Routines Refining the Solution and Estimating Its Error: LAPACK Computational Routines Matrix Inversion: LAPACK Computational Routines Matrix Equilibration: LAPACK Computational Routines
Matrix Factorization: LAPACK Computational Routines x
?getrf ?getrf_batch ?getrf_batch_strided mkl_?getrfnp ?getrfnp_batch_strided mkl_?getrfnpi ?getrf2 ?getri_oop_batch ?getri_oop_batch_strided ?gbtrf ?gttrf ?dttrfb ?potrf ?potrf2 ?pstrf ?pftrf ?pptrf ?pbtrf ?pttrf ?sytrf ?sytrf_aa ?sytrf_rook ?sytrf_rk ?hetrf ?hetrf_aa ?hetrf_rook ?hetrf_rk ?sptrf ?hptrf mkl_?spffrt2, mkl_?spffrtx
Solving Systems of Linear Equations: LAPACK Computational Routines x
?getrs ?getrs_batch_strided ?getrsnp_batch_strided ?gbtrs ?gttrs ?dttrsb ?potrs ?pftrs ?pptrs ?pbtrs ?pttrs ?sytrs ?sytrs_aa ?sytrs_rook ?hetrs ?hetrs_aa ?hetrs_rook ?sytrs2 ?hetrs2 ?sytrs_3 ?hetrs_3 ?sptrs ?hptrs ?trtrs ?tptrs ?tbtrs
Estimating the Condition Number: LAPACK Computational Routines x
?gecon ?gbcon ?gtcon ?pocon ?ppcon ?pbcon ?ptcon ?sycon ?sycon_rook ?sycon_3 ?hecon ?hecon_rook ?hecon_3 ?spcon ?hpcon ?trcon ?tpcon ?tbcon
Refining the Solution and Estimating Its Error: LAPACK Computational Routines x
?gerfs ?gerfsx ?gbrfs ?gbrfsx ?gtrfs ?porfs ?porfsx ?pprfs ?pbrfs ?ptrfs ?syrfs ?syrfsx ?herfs ?herfsx ?sprfs ?hprfs ?trrfs ?tprfs ?tbrfs
Matrix Inversion: LAPACK Computational Routines x
?getri mkl_?getrinp ?potri ?pftri ?pptri ?sytri ?sytri_rook ?hetri ?hetri_rook ?sytri2 ?hetri2 ?sytri2x ?hetri2x ?sytri_3 ?hetri_3 ?sptri ?hptri ?trtri ?tftri ?tptri
Matrix Equilibration: LAPACK Computational Routines x
?geequ ?geequb ?gbequ ?gbequb ?poequ ?poequb ?ppequ ?pbequ ?syequb ?heequb
LAPACK Linear Equation Driver Routines x
?gesv ?gesvx ?gesvxx ?gbsv ?gbsvx ?gbsvxx ?gtsv ?gtsvx ?dtsvb ?posv ?posvx ?posvxx ?ppsv ?ppsvx ?pbsv ?pbsvx ?ptsv ?ptsvx ?sysv ?sysv_aa ?sysv_rook ?sysv_rk ?sysvx ?sysvxx ?hesv ?hesv_aa ?hesv_rk ?hesv_rook ?hesvx ?hesvxx ?spsv ?spsvx ?hpsv ?hpsvx
LAPACK Least Squares and Eigenvalue Problem Routines x
LAPACK Least Squares and Eigenvalue Problem Computational Routines LAPACK Least Squares and Eigenvalue Problem Driver Routines
LAPACK Least Squares and Eigenvalue Problem Computational Routines x
Orthogonal Factorizations: LAPACK Computational Routines Singular Value Decomposition: LAPACK Computational Routines Symmetric Eigenvalue Problems: LAPACK Computational Routines Generalized Symmetric-Definite Eigenvalue Problems: LAPACK Computational Routines Nonsymmetric Eigenvalue Problems: LAPACK Computational Routines Generalized Nonsymmetric Eigenvalue Problems: LAPACK Computational Routines Generalized Singular Value Decomposition: LAPACK Computational Routines Cosine-Sine Decomposition: LAPACK Computational Routines
Orthogonal Factorizations: LAPACK Computational Routines x
?geqrf ?geqr ?geqrfp ?geqrt ?gemqrt ?geqpf ?geqp3 ?orgqr ?ormqr ?gemqr ?ungqr ?unmqr ?gelqf ?gelq ?gelqt ?gemlqt ?orglq ?ormlq ?gemlq ?unglq ?unmlq ?geqlf ?orgql ?ungql ?ormql ?unmql ?gerqf ?orgrq ?ungrq ?ormrq ?unmrq ?tzrzf ?ormrz ?unmrz ?ggqrf ?ggrqf ?tpqrt ?tpmqrt ?tplqt ?tpmlqt
Singular Value Decomposition: LAPACK Computational Routines x
?gebrd ?gbbrd ?orgbr ?ormbr ?ungbr ?unmbr ?bdsqr ?bdsdc
Symmetric Eigenvalue Problems: LAPACK Computational Routines x
?sytrd ?syrdb ?herdb ?orgtr ?ormtr ?hetrd ?ungtr ?unmtr ?orm22/?unm22 ?sptrd ?opgtr ?opmtr ?hptrd ?upgtr ?upmtr ?sbtrd ?hbtrd ?sterf ?steqr ?stemr ?stedc ?stegr ?pteqr ?stebz ?stein ?disna
Generalized Symmetric-Definite Eigenvalue Problems: LAPACK Computational Routines x
?sygst ?hegst ?spgst ?hpgst ?sbgst ?hbgst ?pbstf
Nonsymmetric Eigenvalue Problems: LAPACK Computational Routines x
?gehrd ?orghr ?ormhr ?unghr ?unmhr ?gebal ?gebak ?hseqr ?hsein ?trevc ?trevc3 ?trsna ?trexc ?trsen ?trsyl
Generalized Nonsymmetric Eigenvalue Problems: LAPACK Computational Routines x
?gghrd ?ggbal ?ggbak ?gghd3 ?hgeqz ?tgevc ?tgexc ?tgsen ?tgsyl ?tgsna
Generalized Singular Value Decomposition: LAPACK Computational Routines x
?ggsvp ?ggsvp3 ?ggsvd3 ?tgsja
Cosine-Sine Decomposition: LAPACK Computational Routines x
?bbcsd ?orbdb/?unbdb
LAPACK Least Squares and Eigenvalue Problem Driver Routines x
Linear Least Squares (LLS) Problems: LAPACK Driver Routines Generalized Linear Least Squares (LLS) Problems: LAPACK Driver Routines Symmetric Eigenvalue Problems: LAPACK Driver Routines Nonsymmetric Eigenvalue Problems: LAPACK Driver Routines Singular Value Decomposition: LAPACK Driver Routines Cosine-Sine Decomposition: LAPACK Driver Routines Generalized Symmetric Definite Eigenvalue Problems: LAPACK Driver Routines Generalized Nonsymmetric Eigenvalue Problems: LAPACK Driver Routines
Linear Least Squares (LLS) Problems: LAPACK Driver Routines x
?gels ?gelsy ?gelss ?gelsd ?getsls
Generalized Linear Least Squares (LLS) Problems: LAPACK Driver Routines x
?gglse ?ggglm
Symmetric Eigenvalue Problems: LAPACK Driver Routines x
?syev ?heev ?syevd ?heevd ?syevx ?heevx ?syevr ?heevr ?spev ?hpev ?spevd ?hpevd ?spevx ?hpevx ?sbev ?hbev ?sbevd ?hbevd ?sbevx ?hbevx ?stev ?stevd ?stevx ?stevr
Nonsymmetric Eigenvalue Problems: LAPACK Driver Routines x
?gees ?geesx ?geev ?geevx
Singular Value Decomposition: LAPACK Driver Routines x
?gesvd ?gesdd ?gejsv ?gesvj ?ggsvd ?gesvdx ?bdsvdx
Cosine-Sine Decomposition: LAPACK Driver Routines x
?orcsd/?uncsd ?orcsd2by1/?uncsd2by1
Generalized Symmetric Definite Eigenvalue Problems: LAPACK Driver Routines x
?sygv ?hegv ?sygvd ?hegvd ?sygvx ?hegvx ?spgv ?hpgv ?spgvd ?hpgvd ?spgvx ?hpgvx ?sbgv ?hbgv ?sbgvd ?hbgvd ?sbgvx ?hbgvx
Generalized Nonsymmetric Eigenvalue Problems: LAPACK Driver Routines x
?gges ?ggesx ?gges3 ?ggev ?ggevx ?ggev3
LAPACK Auxiliary Routines x
?lacgv ?lacrm ?lacrt ?laesy ?rot ?spmv ?spr ?syconv ?symv ?syr i?max1 ?sum1 ?gbtf2 ?gebd2 ?gehd2 ?gelq2 ?gelqt3 ?geql2 ?geqr2 ?geqr2p ?geqrt2 ?geqrt3 ?gerq2 ?gesc2 ?getc2 ?getf2 ?gtts2 ?isnan ?laisnan ?labrd ?lacn2 ?lacon ?lacpy ?ladiv ?lae2 ?laebz ?laed0 ?laed1 ?laed2 ?laed3 ?laed4 ?laed5 ?laed6 ?laed7 ?laed8 ?laed9 ?laeda ?laein ?laev2 ?laexc ?lag2 ?lags2 ?lagtf ?lagtm ?lagts ?lagv2 ?lahqr ?lahrd ?lahr2 ?laic1 ?lakf2 ?laln2 ?lals0 ?lalsa ?lalsd ?lamrg ?lamswlq ?lamtsqr ?laneg ?langb ?lange ?langt ?lanhs ?lansb ?lanhb ?lansp ?lanhp ?lanst/?lanht ?lansy ?lanhe ?lantb ?lantp ?lantr ?lanv2 ?lapll ?lapmr ?lapmt ?lapy2 ?lapy3 ?laqgb ?laqge ?laqhb ?laqp2 ?laqps ?laqr0 ?laqr1 ?laqr2 ?laqr3 ?laqr4 ?laqr5 ?laqsb ?laqsp ?laqsy ?laqtr ?laqz0 ?lar1v ?lar2v ?laran ?larf ?larfb ?larfg ?larfgp ?larft ?larfx ?larfy ?large ?largv ?larnd ?larnv ?laror ?larot ?larra ?larrb ?larrc ?larrd ?larre ?larrf ?larrj ?larrk ?larrr ?larrv ?lartg ?lartgp ?lartgs ?lartv ?laruv ?larz ?larzb ?larzt ?las2 ?lascl ?lasd0 ?lasd1 ?lasd2 ?lasd3 ?lasd4 ?lasd5 ?lasd6 ?lasd7 ?lasd8 ?lasd9 ?lasda ?lasdq ?lasdt ?laset ?lasq1 ?lasq2 ?lasq3 ?lasq4 ?lasq5 ?lasq6 ?lasr ?lasrt ?lassq ?lasv2 ?laswlq ?laswp ?lasy2 ?lasyf ?lasyf_aa ?lasyf_rook ?lahef ?lahef_aa ?lahef_rook ?latbs ?latm1 ?latm2 ?latm3 ?latm5 ?latm6 ?latme ?latmr ?latdf ?latps ?latrd ?latrs ?latrz ?latsqr ?lauu2 ?lauum ?orbdb1/?unbdb1 ?orbdb2/?unbdb2 ?orbdb3/?unbdb3 ?orbdb4/?unbdb4 ?orbdb5/?unbdb5 ?orbdb6/?unbdb6 ?org2l/?ung2l ?org2r/?ung2r ?orgl2/?ungl2 ?orgr2/?ungr2 ?orm2l/?unm2l ?orm2r/?unm2r ?orml2/?unml2 ?ormr2/?unmr2 ?ormr3/?unmr3 ?pbtf2 ?potf2 ?ptts2 ?rscl ?syswapr ?heswapr ?syswapr1 ?sygs2/?hegs2 ?sytd2/?hetd2 ?sytf2 ?sytf2_rook ?hetf2 ?hetf2_rook ?tgex2 ?tgsy2 ?trti2 clag2z dlag2s slag2d zlag2c ?larfp ila?lc ila?lr ?gsvj0 ?gsvj1 ?sfrk ?hfrk ?tfsm ?lansf ?lanhf ?tfttp ?tfttr ?tplqt2 ?tpqrt2 ?tprfb ?tpttf ?tpttr ?trttf ?trttp ?pstf2 dlat2s zlat2c ?lacp2 ?la_gbamv ?la_gbrcond ?la_gbrcond_c ?la_gbrcond_x ?la_gbrfsx_extended ?la_gbrpvgrw ?la_geamv ?la_gercond ?la_gercond_c ?la_gercond_x ?la_gerfsx_extended ?la_heamv ?la_hercond_c ?la_hercond_x ?la_herfsx_extended ?la_herpvgrw ?la_lin_berr ?la_porcond ?la_porcond_c ?la_porcond_x ?la_porfsx_extended ?la_porpvgrw ?laqhe ?laqhp ?larcm ?la_gerpvgrw ?larscl2 ?lascl2 ?la_syamv ?la_syrcond ?la_syrcond_c ?la_syrcond_x ?la_syrfsx_extended ?la_syrpvgrw ?la_wwaddw mkl_?tppack mkl_?tpunpack Additional LAPACK Routines
LAPACK Utility Functions and Routines x
ilaver ilaenv iparmq ieeeck ?labad ?lamch ?lamc1 ?lamc2 ?lamc3 ?lamc4 ?lamc5 chla_transtype iladiag ilaprec ilatrans ilauplo xerbla_array
LAPACK Test Functions and Routines x
?latms
ScaLAPACK Routines x
Overview of ScaLAPACK Routines ScaLAPACK Array Descriptors Naming Conventions for ScaLAPACK Routines ScaLAPACK Computational Routines ScaLAPACK Driver Routines ScaLAPACK Auxiliary Routines ScaLAPACK Utility Functions and Routines ScaLAPACK Redistribution/Copy Routines
ScaLAPACK Computational Routines x
Systems of Linear Equations: ScaLAPACK Computational Routines Matrix Factorization: ScaLAPACK Computational Routines Solving Systems of Linear Equations: ScaLAPACK Computational Routines Estimating the Condition Number: ScaLAPACK Computational Routines Refining the Solution and Estimating Its Error: ScaLAPACK Computational Routines Matrix Inversion: ScaLAPACK Computational Routines Matrix Equilibration: ScaLAPACK Computational Routines Orthogonal Factorizations: ScaLAPACK Computational Routines Symmetric Eigenvalue Problems: ScaLAPACK Computational Routines Nonsymmetric Eigenvalue Problems: ScaLAPACK Computational Routines Singular Value Decomposition: ScaLAPACK Driver Routines Generalized Symmetric-Definite Eigenvalue Problems: ScaLAPACK Computational Routines
Matrix Factorization: ScaLAPACK Computational Routines x
p?getrf p?gbtrf p?dbtrf p?dttrf p?potrf p?pbtrf p?pttrf
Solving Systems of Linear Equations: ScaLAPACK Computational Routines x
p?getrs p?gbtrs p?dbtrs p?dttrs p?potrs p?pbtrs p?pttrs p?trtrs
Estimating the Condition Number: ScaLAPACK Computational Routines x
p?gecon p?pocon p?trcon
Refining the Solution and Estimating Its Error: ScaLAPACK Computational Routines x
p?gerfs p?porfs p?trrfs
Matrix Inversion: ScaLAPACK Computational Routines x
p?getri p?potri p?trtri
Matrix Equilibration: ScaLAPACK Computational Routines x
p?geequ p?poequ
Orthogonal Factorizations: ScaLAPACK Computational Routines x
p?geqrf p?geqpf p?orgqr p?ungqr p?ormqr p?unmqr p?gelqf p?orglq p?unglq p?ormlq p?unmlq p?geqlf p?orgql p?ungql p?ormql p?unmql p?gerqf p?orgrq p?ungrq p?ormr3 p?unmr3 p?ormrq p?unmrq p?tzrzf p?ormrz p?unmrz p?ggqrf p?ggrqf
Symmetric Eigenvalue Problems: ScaLAPACK Computational Routines x
p?syngst p?syntrd p?sytrd p?ormtr p?hengst p?hentrd p?hetrd p?unmtr p?stebz p?stedc p?stein
Nonsymmetric Eigenvalue Problems: ScaLAPACK Computational Routines x
p?gehrd p?ormhr p?unmhr p?lahqr p?hseqr p?trevc
Singular Value Decomposition: ScaLAPACK Driver Routines x
p?gebrd p?ormbr p?unmbr
Generalized Symmetric-Definite Eigenvalue Problems: ScaLAPACK Computational Routines x
p?sygst p?hegst
ScaLAPACK Driver Routines x
p?geevx p?gesv p?gesvx p?gbsv p?dbsv p?dtsv p?posv p?posvx p?pbsv p?ptsv p?gels p?syev p?syevd p?syevr p?syevx p?heev p?heevd p?heevr p?heevx p?gesvd p?sygvx p?hegvx
ScaLAPACK Auxiliary Routines x
b?laapp b?laexc b?trexc p?lacgv p?max1 pilaver pmpcol pmpim2 ?combamax1 p?sum1 p?dbtrsv p?dttrsv p?gebal p?gebd2 p?gehd2 p?gelq2 p?geql2 p?geqr2 p?gerq2 p?getf2 p?labrd p?lacon p?laconsb p?lacp2 p?lacp3 p?lacpy p?laevswp p?lahrd p?laiect p?lamve p?lange p?lanhs p?lansy, p?lanhe p?lantr p?lapiv p?lapv2 p?laqge p?laqr0 p?laqr1 p?laqr2 p?laqr3 p?laqr4 p?laqr5 p?laqsy p?lared1d p?lared2d p?larf p?larfb p?larfc p?larfg p?larft p?larz p?larzb p?larzc p?larzt p?lascl p?lase2 p?laset p?lasmsub p?lasrt p?lassq p?laswp p?latra p?latrd p?latrs p?latrz p?lauu2 p?lauum p?lawil p?org2l/p?ung2l p?org2r/p?ung2r p?orgl2/p?ungl2 p?orgr2/p?ungr2 p?orm2l/p?unm2l p?orm2r/p?unm2r p?orml2/p?unml2 p?ormr2/p?unmr2 p?pbtrsv p?pttrsv p?potf2 p?rot p?rscl p?sygs2/p?hegs2 p?sytd2/p?hetd2 p?trord p?trsen p?trti2 ?lahqr2 ?lamsh ?lapst ?laqr6 ?lar1va ?laref ?larrb2 ?larrd2 ?larre2 ?larre2a ?larrf2 ?larrv2 ?lasorte ?lasrt2 ?stegr2 ?stegr2a ?stegr2b ?stein2 ?dbtf2 ?dbtrf ?dttrf ?dttrsv ?pttrsv ?steqr2 ?trmvt pilaenv pilaenvx pjlaenv Additional ScaLAPACK Routines
ScaLAPACK Utility Functions and Routines x
p?labad p?lachkieee p?lamch p?lasnbt descinit numroc
ScaLAPACK Redistribution/Copy Routines x
p?gemr2d p?trmr2d
Sparse Solver Routines x
oneMKL PARDISO - Parallel Direct Sparse Solver Interface Parallel Direct Sparse Solver for Clusters Interface Direct Sparse Solver (DSS) Interface Routines Iterative Sparse Solvers based on Reverse Communication Interface (RCI ISS) Preconditioners based on Incomplete LU Factorization Technique Sparse Matrix Checker Routines
oneMKL PARDISO - Parallel Direct Sparse Solver Interface x
pardiso pardisoinit pardiso_64 mkl_pardiso_pivot pardiso_getdiag pardiso_export pardiso_handle_store pardiso_handle_restore pardiso_handle_delete pardiso_handle_store_64 pardiso_handle_restore_64 pardiso_handle_delete_64 oneMKL PARDISO Parameters in Tabular Form pardiso iparm Parameter PARDISO_DATA_TYPE
Parallel Direct Sparse Solver for Clusters Interface x
cluster_sparse_solver cluster_sparse_solver_64 cluster_sparse_solver_get_csr_size cluster_sparse_solver_set_csr_ptrs cluster_sparse_solver_set_ptr cluster_sparse_solver_export cluster_sparse_solver iparm Parameter
Direct Sparse Solver (DSS) Interface Routines x
DSS Interface Description DSS Implementation Details DSS Routines
DSS Routines x
dss_create dss_define_structure dss_reorder dss_factor_real, dss_factor_complex dss_solve_real, dss_solve_complex dss_delete dss_statistics mkl_cvt_to_null_terminated_str
Iterative Sparse Solvers based on Reverse Communication Interface (RCI ISS) x
CG Interface Description FGMRES Interface Description RCI ISS Routines RCI ISS Implementation Details
RCI ISS Routines x
dcg_init dcg_check dcg dcg_get dcgmrhs_init dcgmrhs_check dcgmrhs dcgmrhs_get dfgmres_init dfgmres_check dfgmres dfgmres_get
Preconditioners based on Incomplete LU Factorization Technique x
ILU0 and ILUT Preconditioners Interface Description dcsrilu0 dcsrilut
Sparse Matrix Checker Routines x
sparse_matrix_checker sparse_matrix_checker_init
Extended Eigensolver Routines x
The FEAST Algorithm Extended Eigensolver Functionality Extended Eigensolver Interfaces for Eigenvalues within Interval Extended Eigensolver Interfaces for Extremal Eigenvalues/Singular Values
Extended Eigensolver Functionality x
Parallelism in Extended Eigensolver Routines Achieving Performance With Extended Eigensolver Routines
Extended Eigensolver Interfaces for Eigenvalues within Interval x
Extended Eigensolver Naming Conventions feastinit Extended Eigensolver Input Parameters Extended Eigensolver Output Details Extended Eigensolver RCI Routines Extended Eigensolver Predefined Interfaces
Extended Eigensolver RCI Routines x
Extended Eigensolver RCI Interface Description ?feast_srci/?feast_hrci
Extended Eigensolver Predefined Interfaces x
Matrix Storage ?feast_syev/?feast_heev ?feast_sygv/?feast_hegv ?feast_sbev/?feast_hbev ?feast_sbgv/?feast_hbgv ?feast_scsrev/?feast_hcsrev ?feast_scsrgv/?feast_hcsrgv
Extended Eigensolver Interfaces for Extremal Eigenvalues/Singular Values x
Extended Eigensolver Interfaces to find largest/smallest eigenvalues Extended Eigensolver Interfaces to find largest/smallest singular values mkl_sparse_ee_init Extended Eigensolver Input Parameters for Extremal Eigenvalue Problem
Extended Eigensolver Interfaces to find largest/smallest eigenvalues x
mkl_sparse_?_ev mkl_sparse_?_gv
Extended Eigensolver Interfaces to find largest/smallest singular values x
mkl_sparse_?_svd
Vector Mathematical Functions x
VM Data Types, Accuracy Modes, and Performance Tips VM Naming Conventions Vector Indexing Methods VM Error Diagnostics VM Mathematical Functions VM Pack/Unpack Functions VM Service Functions Miscellaneous VM Functions
VM Naming Conventions x
VM Function Interfaces
VM Function Interfaces x
VM Mathematical Function Interfaces VM Pack Function Interfaces VM Unpack Function Interfaces VM Service Function Interfaces VM Input Parameters VM Output Parameters
VM Mathematical Functions x
Special Value Notations Arithmetic Functions Power and Root Functions Exponential and Logarithmic Functions Trigonometric Functions Hyperbolic Functions Special Functions Rounding Functions
Arithmetic Functions x
v?Add v?Sub v?Sqr v?Mul v?MulByConj v?Conj v?Abs v?Arg v?LinearFrac v?Fmod v?Remainder
Power and Root Functions x
v?Inv v?Div v?Sqrt v?InvSqrt v?Cbrt v?InvCbrt v?Pow2o3 v?Pow3o2 v?Pow v?Powx v?Powr v?Hypot
Exponential and Logarithmic Functions x
v?Exp v?Exp2 v?Exp10 v?Expm1 v?Ln v?Log2 v?Log10 v?Log1p v?Logb
Trigonometric Functions x
v?Cos v?Sin v?SinCos v?CIS v?Tan v?Acos v?Asin v?Atan v?Atan2 v?Cospi v?Sinpi v?Tanpi v?Acospi v?Asinpi v?Atanpi v?Atan2pi v?Cosd v?Sind v?Tand
Hyperbolic Functions x
v?Cosh v?Sinh v?Tanh v?Acosh v?Asinh v?Atanh
Special Functions x
v?Erf v?Erfc v?CdfNorm v?ErfInv v?ErfcInv v?CdfNormInv v?LGamma v?TGamma v?ExpInt1
Rounding Functions x
v?Floor v?Ceil v?Trunc v?Round v?NearbyInt v?Rint v?Modf v?Frac
VM Pack/Unpack Functions x
v?Pack v?Unpack
VM Service Functions x
vmlSetMode vmlgetmode vmlSetErrStatus vmlgeterrstatus vmlclearerrstatus vmlSetErrorCallBack vmlGetErrorCallBack vmlClearErrorCallBack
Miscellaneous VM Functions x
v?CopySign v?NextAfter v?Fdim v?Fmax v?Fmin v?MaxMag v?MinMag
Statistical Functions x
Random Number Generators Convolution and Correlation Summary Statistics
Random Number Generators x
Random Number Generators Conventions Basic Generators Error Reporting VS RNG Usage ModelIntel® oneMKL RNG Usage Model Service Routines Distribution Generators Advanced Service Routines
Random Number Generators Conventions x
Random Number Generators Mathematical Notation Random Number Generators Naming Conventions
Basic Generators x
BRNG Parameter Definition Random Streams BRNG Data Types
Service Routines x
vslNewStream vslNewStreamEx vsliNewAbstractStream vsldNewAbstractStream vslsNewAbstractStream vslDeleteStream vslCopyStream vslCopyStreamState vslSaveStreamF vslLoadStreamF vslSaveStreamM vslLoadStreamM vslGetStreamSize vslLeapfrogStream vslSkipAheadStream vslSkipAheadStreamEx vslGetStreamStateBrng vslGetNumRegBrngs
Distribution Generators x
Continuous Distributions Discrete Distributions
Continuous Distributions x
vRngUniform Continuous Distribution Generators vRngGaussian vRngGaussianMV vRngExponential vRngLaplace vRngWeibull vRngCauchy vRngRayleigh vRngLognormal vRngGumbel vRngGamma vRngBeta vRngChiSquare
Discrete Distributions x
vRngUniform Discrete Distribution Generators vRngUniformBits vRngUniformBits32 vRngUniformBits64 vRngBernoulli vRngGeometric vRngBinomial vRngHypergeometric vRngPoisson vRngPoissonV vRngNegBinomial vRngMultinomial
Advanced Service Routines x
Advanced Service Routine Data Types vslGetBrngProperties
Convolution and Correlation x
Convolution and Correlation Naming Conventions Convolution and Correlation Data Types Convolution and Correlation Parameters Convolution and Correlation Task Status and Error Reporting Convolution and Correlation Task Constructors Convolution and Correlation Task Editors Task Execution Routines Convolution and Correlation Task Destructors Convolution and Correlation Task Copiers Convolution and Correlation Usage Examples Convolution and Correlation Mathematical Notation and Definitions Convolution and Correlation Data Allocation
Convolution and Correlation Task Constructors x
vslConvNewTask/vslCorrNewTask vslConvNewTask1D/vslCorrNewTask1D vslConvNewTaskX/vslCorrNewTaskX vslConvNewTaskX1D/vslCorrNewTaskX1D
Convolution and Correlation Task Editors x
vslConvSetMode/vslCorrSetMode vslConvSetInternalPrecision/vslCorrSetInternalPrecision vslConvSetStart/vslCorrSetStart vslConvSetDecimation/vslCorrSetDecimation
Task Execution Routines x
vslConvExec/vslCorrExec vslConvExec1D/vslCorrExec1D vslConvExecX/vslCorrExecX vslConvExecX1D/vslCorrExecX1D
Convolution and Correlation Task Destructors x
vslConvDeleteTask/vslCorrDeleteTask
Convolution and Correlation Task Copiers x
vslConvCopyTask/vslCorrCopyTask
Summary Statistics x
Summary Statistics Naming Conventions Summary Statistics Data Types Summary Statistics Parameters Summary Statistics Task Status and Error Reporting Summary Statistics Task Constructors Summary Statistics Task Editors Summary Statistics Task Computation Routines Summary Statistics Task Destructor Summary Statistics Usage Examples Summary Statistics Mathematical Notation and Definitions
Summary Statistics Task Constructors x
vslSSNewTask
Summary Statistics Task Editors x
vslSSEditTask vslSSEditMoments vslSSEditSums vslSSEditCovCor vslSSEditCP vslSSEditPartialCovCor vslSSEditQuantiles vslSSEditStreamQuantiles vslSSEditPooledCovariance vslSSEditRobustCovariance vslSSEditOutliersDetection vslSSEditMissingValues vslSSEditCorParameterization
Summary Statistics Task Computation Routines x
vslSSCompute
Summary Statistics Task Destructor x
vslSSDeleteTask
Fourier Transform Functions x
FFT Functions Cluster FFT Functions
FFT Functions x
FFT Interface Computing an FFT Configuration Settings FFT Descriptor Manipulation Functions FFT Descriptor Configuration Functions FFT Computation Functions Status Checking Functions
Configuration Settings x
DFTI_PRECISION DFTI_FORWARD_DOMAIN DFTI_DIMENSION, DFTI_LENGTHS DFTI_PLACEMENT DFTI_FORWARD_SCALE, DFTI_BACKWARD_SCALE DFTI_NUMBER_OF_USER_THREADS DFTI_THREAD_LIMIT DFTI_INPUT_STRIDES, DFTI_OUTPUT_STRIDES DFTI_NUMBER_OF_TRANSFORMS DFTI_INPUT_DISTANCE, DFTI_OUTPUT_DISTANCE DFTI_COMPLEX_STORAGE, DFTI_REAL_STORAGE, DFTI_CONJUGATE_EVEN_STORAGE DFTI_PACKED_FORMAT DFTI_WORKSPACE DFTI_COMMIT_STATUS DFTI_ORDERING
FFT Descriptor Manipulation Functions x
DftiCreateDescriptor DftiCommitDescriptor DftiFreeDescriptor DftiCopyDescriptor
FFT Descriptor Configuration Functions x
DftiSetValue DftiGetValue
FFT Computation Functions x
DftiComputeForward DftiComputeBackward Configuring and Computing an FFT in Fortran
Status Checking Functions x
DftiErrorClass DftiErrorMessage
Cluster FFT Functions x
Computing Cluster FFT Distributing Data Among Processes Cluster FFT Interface Cluster FFT Descriptor Manipulation Functions Cluster FFT Computation Functions Cluster FFT Descriptor Configuration Functions Error Codes
Cluster FFT Descriptor Manipulation Functions x
DftiCreateDescriptorDM DftiCommitDescriptorDM DftiFreeDescriptorDM
Cluster FFT Computation Functions x
DftiComputeForwardDM DftiComputeBackwardDM
Cluster FFT Descriptor Configuration Functions x
DftiSetValueDM DftiGetValueDM
PBLAS Routines x
PBLAS Routines Overview PBLAS Routine Naming Conventions PBLAS Level 1 Routines PBLAS Level 2 Routines PBLAS Level 3 Routines
PBLAS Level 1 Routines x
p?amax p?asum p?axpy p?copy p?dot p?dotc p?dotu p?nrm2 p?scal p?swap
PBLAS Level 2 Routines x
p?gemv p?agemv p?ger p?gerc p?geru p?hemv p?ahemv p?her p?her2 p?symv p?asymv p?syr p?syr2 p?trmv p?atrmv p?trsv
PBLAS Level 3 Routines x
p?geadd p?tradd p?gemm p?hemm p?herk p?her2k p?symm p?syrk p?syr2k p?tran p?tranu p?tranc p?trmm p?trsm
Partial Differential Equations Support x
Trigonometric Transform Routines Fast Poisson Solver Routines Calling PDE Support Routines from Fortran
Trigonometric Transform Routines x
Trigonometric Transforms Implemented Sequence of Invoking TT Routines Trigonometric Transform Interface Description TT Routines Common Parameters of the Trigonometric Transforms Trigonometric Transform Implementation Details
TT Routines x
?_init_trig_transform ?_commit_trig_transform ?_forward_trig_transform ?_backward_trig_transform free_trig_transform
Fast Poisson Solver Routines x
Poisson Solver Implementation Sequence of Invoking Poisson Solver Routines Fast Poisson Solver Interface Description Routines for the Cartesian Solver Routines for the Spherical Solver Common Parameters for the Poisson Solver Poisson Solver Implementation Details
Routines for the Cartesian Solver x
?_init_Helmholtz_2D/?_init_Helmholtz_3D _commit_Helmholtz_2D/?_commit_Helmholtz_3D ?_Helmholtz_2D/?_Helmholtz_3D free_Helmholtz_2D/free_Helmholtz_3D
Routines for the Spherical Solver x
?_init_sph_p/?_init_sph_np ?_commit_sph_p/?_commit_sph_np ?_sph_p/?_sph_np free_sph_p/free_sph_np
Common Parameters for the Poisson Solver x
ipar dpar and spar Caveat on Parameter Modifications Parameters That Define Boundary Conditions
Nonlinear Optimization Problem Solvers x
Nonlinear Solver Organization and Implementation Nonlinear Solver Routine Naming Conventions Nonlinear Least Squares Problem without Constraints Nonlinear Least Squares Problem with Linear (Bound) Constraints Jacobian Matrix Calculation Routines
Nonlinear Least Squares Problem without Constraints x
?trnlsp_init ?trnlsp_check ?trnlsp_solve ?trnlsp_get ?trnlsp_delete
Nonlinear Least Squares Problem with Linear (Bound) Constraints x
?trnlspbc_init ?trnlspbc_check ?trnlspbc_solve ?trnlspbc_get ?trnlspbc_delete
Jacobian Matrix Calculation Routines x
?jacobi_init ?jacobi_solve ?jacobi_delete ?jacobi ?jacobix
Support Functions x
Using a Fortran Interface Module for Support Functions Version Information Threading Control Error Handling Character Equality Testing Timing Memory Management Single Dynamic Library Control Conditional Numerical Reproducibility Control Miscellaneous
Version Information x
mkl_get_version_string
Threading Control x
mkl_set_num_threads mkl_domain_set_num_threads mkl_set_num_threads_local mkl_set_dynamic mkl_get_max_threads mkl_domain_get_max_threads mkl_get_dynamic mkl_set_num_stripes mkl_get_num_stripes
Error Handling x
Error Handling for Linear Algebra Routines Handling Fatal Errors
Error Handling for Linear Algebra Routines x
xerbla pxerbla
Handling Fatal Errors x
mkl_set_exit_handler
Character Equality Testing x
lsame lsamen
Timing x
second/dsecnd mkl_get_cpu_clocks mkl_get_cpu_frequency mkl_get_max_cpu_frequency mkl_get_clocks_frequency
Memory Management x
mkl_free_buffers mkl_thread_free_buffers mkl_disable_fast_mm mkl_mem_stat mkl_peak_mem_usage mkl_malloc mkl_calloc mkl_realloc mkl_free mkl_set_memory_limit Usage Examples for the Memory Functions
Single Dynamic Library Control x
mkl_set_interface_layer mkl_set_threading_layer mkl_set_xerbla mkl_set_progress mkl_set_pardiso_pivot
Conditional Numerical Reproducibility Control x
mkl_cbwr_set mkl_cbwr_get mkl_cbwr_get_auto_branch Named Constants for CNR Control Reproducibility Conditions Usage Examples for CNR Support Functions
Miscellaneous x
mkl_progress mkl_enable_instructions mkl_set_env_mode mkl_verbose mkl_verbose_output_file mkl_set_mpi mkl_finalize
BLACS Routines x
Matrix Shapes Repeatability and Coherence BLACS Combine Operations BLACS Point To Point Communication BLACS Broadcast Routines BLACS Support Routines Examples of BLACS Routines Usage
BLACS Combine Operations x
?gamx2d ?gamn2d ?gsum2d
BLACS Point To Point Communication x
?gesd2d ?trsd2d ?gerv2d ?trrv2d
BLACS Broadcast Routines x
?gebs2d ?trbs2d ?gebr2d ?trbr2d
BLACS Support Routines x
Initialization Routines Destruction Routines Informational Routines Miscellaneous Routines
Initialization Routines x
blacs_pinfo blacs_setup blacs_get blacs_set blacs_gridinit blacs_gridmap
Destruction Routines x
blacs_freebuff blacs_gridexit blacs_abort blacs_exit
Informational Routines x
blacs_gridinfo blacs_pnum blacs_pcoord
Miscellaneous Routines x
blacs_barrier
Data Fitting Functions x
Data Fitting Function Naming Conventions Data Fitting Function Data Types Mathematical Conventions for Data Fitting Functions Data Fitting Usage Model Data Fitting Usage Examples Data Fitting Function Task Status and Error Reporting Data Fitting Task Creation and Initialization Routines Task Configuration Routines Data Fitting Computational Routines Data Fitting Task Destructors
Data Fitting Task Creation and Initialization Routines x
df?newtask1d
Task Configuration Routines x
df?editppspline1d df?editptr dfieditval df?editidxptr df?queryptr dfiqueryval df?queryidxptr
Data Fitting Computational Routines x
df?construct1d df?interpolate1d/df?interpolateex1d df?integrate1d/df?integrateex1d df?searchcells1d/df?searchcellsex1d df?interpcallback df?integrcallback df?searchcellscallback
Data Fitting Task Destructors x
dfdeletetask
Appendix A: Linear Solvers Basics x
Sparse Linear Systems Sparse Matrix Storage Formats
Sparse Linear Systems x
Matrix Fundamentals Direct Method
Sparse Matrix Storage Formats x
DSS Symmetric Matrix Storage DSS Nonsymmetric Matrix Storage DSS Structurally Symmetric Matrix Storage DSS Distributed Symmetric Matrix Storage Sparse BLAS CSR Matrix Storage Format Sparse BLAS CSC Matrix Storage Format Sparse BLAS Coordinate Matrix Storage Format Sparse BLAS Diagonal Matrix Storage Format Sparse BLAS Skyline Matrix Storage Format Sparse BLAS BSR Matrix Storage Format
Appendix B: Routine and Function Arguments x
Vector Arguments in BLAS Vector Arguments in Vector Math Matrix Arguments
Appendix D: FFTW Interface to Intel® Math Kernel Library x
FFTW Notational Conventions FFTW2 Interface to Intel® oneAPI Math Kernel Library FFTW3 Interface to Intel® oneAPI Math Kernel Library
FFTW2 Interface to Intel® oneAPI Math Kernel Library x
Wrappers Reference Calling FFTW2 Interface Wrappers from Fortran Limitations of the FFTW2 Interface to Intel® oneAPI Math Kernel Library (oneMKL) Installing FFTW2 Interface Wrappers
Wrappers Reference x
One-dimensional Complex-to-complex FFTs Multi-dimensional Complex-to-complex FFTs One-dimensional Real-to-half-complex/Half-complex-to-real FFTs Multi-dimensional Real-to-complex/Complex-to-real FFTs Multi-threaded FFTW FFTW Support Functions
Installing FFTW2 Interface Wrappers x
Creating the Wrapper Library Application Assembling Running FFTW2 Interface Wrapper Examples
FFTW3 Interface to Intel® oneAPI Math Kernel Library x
Using FFTW3 Wrappers Calling FFTW3 Interface Wrappers from Fortran Building Your Own FFTW3 Interface Wrapper Library Building an Application With FFTW3 Interface Wrappers Running FFTW3 Interface Wrapper Examples MPI FFTW3 Wrappers
MPI FFTW3 Wrappers x
Building Your Own Wrapper Library Building an Application Running Examples
Appendix E: Code Examples x
BLAS Code Examples Fourier Transform Functions Code Examples
Fourier Transform Functions Code Examples x
FFT Code Examples Examples for Cluster FFT Functions Auxiliary Data Transformations
FFT Code Examples x
Examples of Using OpenMP* Threading for FFT Computation
Appendix F: oneMKL Functionality x
BLAS Functionality Transposition Functionality LAPACK Functionality DFT Functionality Sparse BLAS Functionality Sparse Solvers Functionality Graphs Functionality Random Number Generators Functionality Vector Math Functionality Data Fitting Functionality Summary Statistics Functionality
Developer Reference for Intel® oneAPI Math Kernel Library - Fortran

Error Analysis

In practice, most computations are performed with rounding errors. Besides, you often need to solve a system Ax = b, where the data (the elements of A and b) are not known exactly. Therefore, it is important to understand how the data errors and rounding errors can affect the solution x.

Data perturbations. If x is the exact solution of Ax = b, and x + δx is the exact solution of a perturbed problem (A + δA)(x + δx) = (b + δb), then this estimate, given up to linear terms of perturbations, holds:


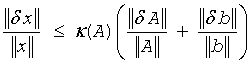
Equation

where A + δA is nonsingular and

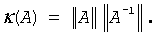
Equation

In other words, relative errors in A or b may be amplified in the solution vector x by a factor κ(A) = ||A|| ||A-1|| called the condition number of A.

Rounding errors have the same effect as relative perturbations c(n)ε in the original data. Here ε is the machine precision, defined as the smallest positive number x such that 1 + x > 1; and c(n) is a modest function of the matrix order n. The corresponding solution error is

||δx||/||x||≤c(n)κ(A)ε. (The value of c(n) is seldom greater than 10n.)

NOTE:

Machine precision depends on the data type used.

Thus, if your matrix A is ill-conditioned (that is, its condition number κ(A) is very large), then the error in the solution x can also be large; you might even encounter a complete loss of precision. LAPACK provides routines that allow you to estimate κ(A) (see Routines for Estimating the Condition Number) and also give you a more precise estimate for the actual solution error (see Refining the Solution and Estimating Its Error).

Parent topic: LAPACK Routines
Level Two Title