Notes for Intel® oneAPI Math Kernel Library Vector Statistics

Download PDF
ID 772987
Date 12/04/2020
Public

A newer version of this document is available. Customers should click here to go to the newest version.

Document Table of Contents
Document Table of Contents x
Notes for Intel® oneAPI Math Kernel Library Vector Statistics
Notes for Intel® oneAPI Math Kernel Library Vector Statistics x
Introduction Randomness and Scientific Experiment Random Numbers Figures of Merit for Random Number Generators Vector Statistics Structure Testing of Basic Random Number Generators Testing of Distribution Random Number Generators Bibliography Notices and Disclaimers
Introduction x
What's New About Vector Statistics About This Document Conventions
Figures of Merit for Random Number Generators x
Uniform Probability Distribution and Basic Pseudo- and Quasi-Random Number Generators Figures of Merit for General (Non-Uniform) Distribution Generators
Vector Statistics Structure x
Why Vector Type Generators? Basic Random Number Generators Random Streams and RNGs in Parallel Computation Generating Methods for Random Numbers of Non-Uniform Distribution Accurate and Fast Modes of Random Number Generation Example of VS Use
Random Streams and RNGs in Parallel Computation x
Initializing a BRNG Creating and Initializing Random Streams Creating Random Stream Copy and Copying Stream State Saving and Restoring Random Streams Independent Streams. Block-Splitting and Leapfrogging Abstract Basic Random Number Generators. Abstract Streams
Generating Methods for Random Numbers of Non-Uniform Distribution x
Inverse Transformation Acceptance/Rejection Mixture of Distributions Special Properties
Testing of Basic Random Number Generators x
BRNG Implementations and Categories Interpreting Test Results BRNG Test Descriptions BRNG Properties and Testing Results
Interpreting Test Results x
One-Level (Threshold) Testing Two-Level Testing
BRNG Test Descriptions x
3D Spheres Test Birthday Spacing Test Bitstream Test Rank of 31x31 Binary Matrices Test Rank of 32x32 Binary Matrices Test Rank of 6x8 Binary Matrices Test Count-the-1's Test (Stream of Bits) Count-the-1's Test (Stream of Specific Bytes) Craps Test Parking Lot Test Self-Avoiding Random Walk Test Template Test
BRNG Properties and Testing Results x
MCG31m1 R250 MRG32k3a MCG59 WH MT19937 SFMT19937 MT2203 SOBOL NIEDERREITER Philox4x32-10 ARS5
Testing of Distribution Random Number Generators x
Interpreting Test Results Description of Distribution Generator Tests Continuous Distribution Random Number Generators Discrete Distribution Random Number Generators
Description of Distribution Generator Tests x
Confidence Test Distribution Moments Test Chi-Squared Goodness-of-Fit Test Performance
Continuous Distribution Random Number Generators x
Uniform (VSL_RNG_METHOD_UNIFORM_STD/VSL_RNG_METHOD_UNIFORM_STD_ACCURATE) Gaussian (VSL_RNG_METHOD_GAUSSIAN_BOXMULLER) Gaussian (VSL_RNG_METHOD_GAUSSIAN_BOXMULLER2) Gaussian (VSL_RNG_METHOD_GAUSSIAN_ICDF) GaussianMV (VSL_RNG_METHOD_GAUSSIANMV_BOXMULLER) GaussianMV (VSL_RNG_METHOD_GAUSSIANMV_BOXMULLER2) GaussianMV  (VSL_RNG_METHOD_GAUSSIANMV_ICDF) Exponential (VSL_RNG_METHOD_EXPONENTIAL_ICDF/VSL_RNG_METHOD_EXPONENTIAL_ICDF_ACCURATE) Laplace (VSL_RNG_METHOD_LAPLACE_ICDF) Weibull (VSL_RNG_METHOD_WEIBULL_ICDF/ VSL_RNG_METHOD_WEIBULL_ICDF_ACCURATE) Cauchy (VSL_RNG_METHOD_CAUCHY_ICDF) Rayleigh (VSL_RNG_METHOD_RAYLEIGH_ICDF/ VSL_RNG_METHOD_RAYLEIGH_ICDF_ACCURATE) Lognormal (VSL_RNG_METHOD_LOGNORMAL_ BOXMULLER2/VSL_RNG_METHOD_LOGNORMAL_BOXMULLER2_ACCURATE) Lognormal (VSL_RNG_METHOD_LOGNORMAL_ICDF/VSL_RNG_METHOD_LOGNORMAL_ICDF_ACCURATE) Gumbel (VSL_RNG_METHOD_GUMBEL_ICDF) Gamma (VSL_RNG_METHOD_GAMMA_GNORM/ VSL_RNG_METHOD_GAMMA_GNORM_ACCURATE) Beta (VSL_RNG_METHOD_BETA_CJA/ VSL_RNG_METHOD_BETA_CJA_ACCURATE) ChiSquare (VSL_RNG_METHOD_CHISQUARE_CHI2GAMMA)
Discrete Distribution Random Number Generators x
Uniform (VSL_RNG_METHOD_UNIFORM_STD) UniformBits (VSL_RNG_METHOD_UNIFORMBITS_STD) UniformBits32 (VSL_RNG_METHOD_UNIFORMBITS32_STD) UniformBits64 (VSL_RNG_METHOD_UNIFORMBITS64_STD) Bernoulli (VSL_RNG_METHOD_BERNOULLI_ICDF) Geometric (VSL_RNG_METHOD_GEOMETRIC_ICDF) Binomial (VSL_RNG_METHOD_BINOMIAL_BTPE) Hypergeometric (VSL_RNG_METHOD_HYPERGEOMETRIC_H2PE) Poisson (VSL_RNG_METHOD_POISSON_PTPE) Poisson (VSL_RNG_METHOD_POISSON_POISNORM) PoissonV (VSL_RNG_METHOD_POISSONV_POISNORM) NegBinomial (VSL_RNG_METHOD_NEGBINOMIAL_NBAR) Multinomial (VSL_RNG_METHOD_MULTINOMIAL_MULTPOISSON)
Notes for Intel® oneAPI Math Kernel Library Vector Statistics

ChiSquare (VSL_RNG_METHOD_CHISQUARE_CHI2GAMMA)

Random number generator of the chi-square distribution with degrees of freedom v. You can generate any successful random number x of the chi-square distribution as follows:

  1. If v = 1 and v = 3, a chi-square distributed number is generated as a sum of squares of v independent normal random numbers with parameter mean value a = 0 and standard deviation σ = 1.
  2. If v is even and 2 ≤ v ≤ 16, a chi-square distributed random number is generated according to the formula:

    , where ui is a vector of successive random numbers uniformly distributed over the interval (0, 1).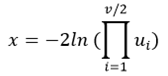
  3. If v ≥ 17 or v is odd and 5 ≤ v ≤ 15, the ChiSquare distribution is reduced to Gamma distribution with parameters shape α = v/2, offset a = 0, and scalefactor β = 2. Random numbers of the Gamma distribution are generated using method VSL_RNG_METHOD_GAMMA_GNORM.

See Intel® oneAPI Math Kernel Library Vector Statistics Random Number Generator Performance Data for test results summary and performance graphs.

Parent topic: Continuous Distribution Random Number Generators
Level Two Title