Accelerating the 2D Fourier Correlation Algorithm with ArrayFire and oneAPI

Implement the Fourier Correlation Algorithm Using oneAPI (The Parallel Universe, Issue 44) showed how to compute the 1D cross-correlation of two signals using a combination of SYCL and oneMKL functions. The present article looks at 2D cross-correlation to find the best overlap of two similar images (Figure 1). In addition to illustrating a 2D use case, this article expands on the previous work by comparing two approaches to write once, run anywhere heterogeneous parallelism: oneAPI and ArrayFire.

Editor’s note: Readers may be interested in ArrayFire Interoperability with oneAPI, Libraries, and OpenCL (The Parallel Universe, Issue 47).

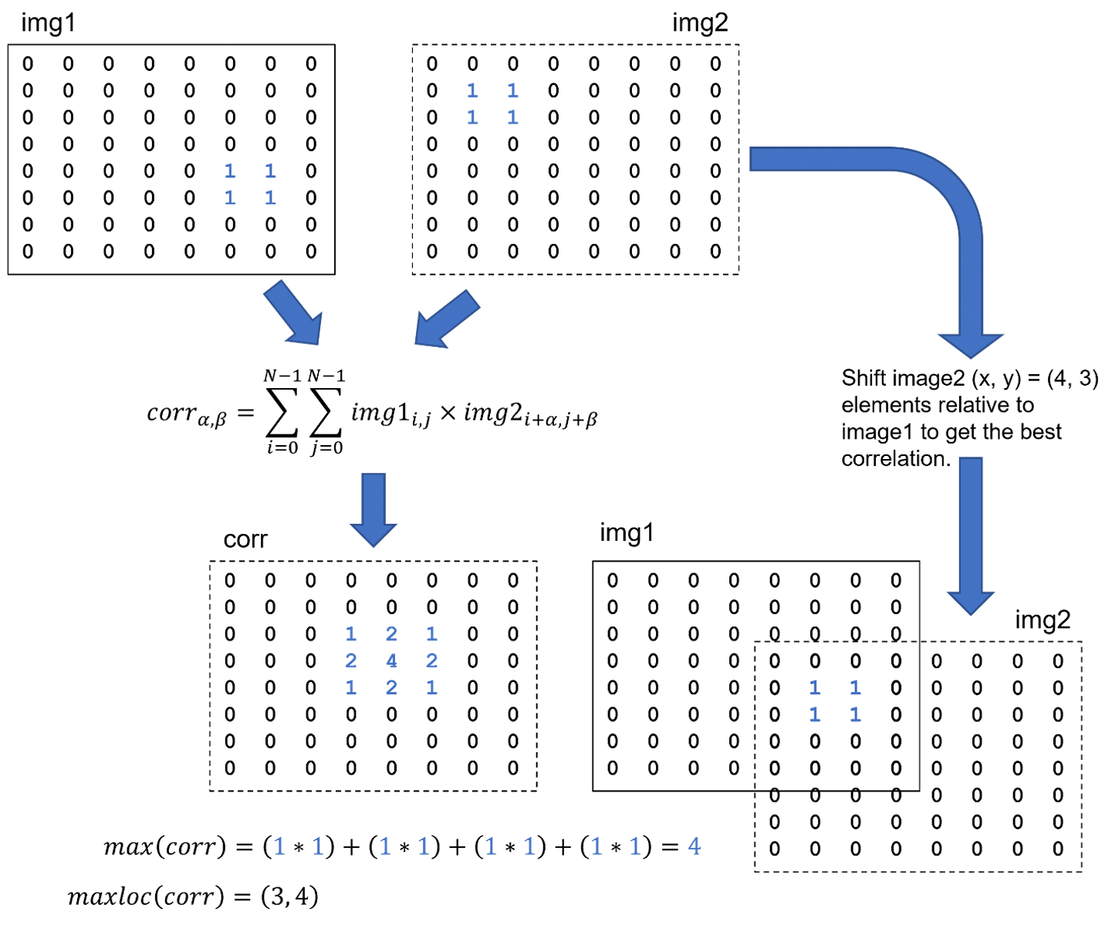
Figure 1. Finding the optimal alignment of two images (represented as binary, square matrices), where (α, β) is the displacement of img2 relative to img1. Note that the second image is circularly shifted when computing the correlation.

The brute force summation shown in Figure 1 is inefficient and possibly infeasible for large problems, so like the previous 1D example, the 2D cross-correlation will also take advantage of the Fourier correlation algorithm to significantly reduce the computational complexity (Figure 2). The 2D Fourier correlation is implemented using both approaches, and the codes are shown side-by-side to illustrate their differences and relative strengths.

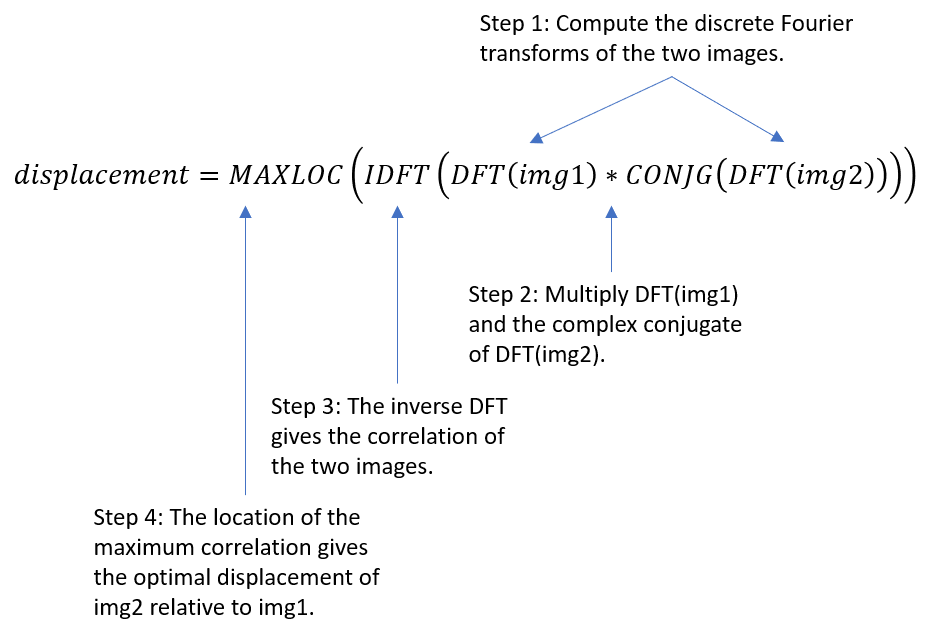
Figure 2. The Fourier correlation algorithm in four steps. DFT is the discrete Fourier transform, IDFT is the inverse DFT, CONJG is the complex conjugate, and MAXLOC is the location of the maximum correlation score.

The 2D oneAPI implementation also illustrates differences and improvements over the previous 1D implementation. First, multidimensional Fourier transforms in oneMKL must account for data layout in the real and complex domains. This is demonstrated in the oneAPI examples below. Second, the 1D implementation used a MAXLOC reduction operator written in SYCL. The 2D implementation replaces this code with standard functions from the oneAPI DPC++ Library (oneDPL). This makes the code clearer and much more succinct.

Implementing the Fourier Correlation Algorithm

Ideally, the entire computation should be performed on the device once the images are loaded into the device memory. Only the final displacement (two scalars in the 2D correlation) is needed by the host. Any other host-device data transfer is unnecessary, and will hurt performance, especially if the images are large

Accelerator Offload with ArrayFire

It is easy to implement the Fourier correlation algorithm in ArrayFire because each step in Figure 2 practically maps to a single statement (Figure 3). Even without the comments, this code should be readable by programmers familiar with C++ or MATLAB, Fortran, and NumPy array notation. There are no explicit loops in this code, and there is no explicit host-device data transfer or device offload. The coding abstraction is implicitly data parallel, so these details are handled by the ArrayFire runtime library.

Figure 3. Fourier correlation algorithm implemented using ArrayFire.

Most ArrayFire functions are asynchronous, so the caller proceeds without waiting for the function to return. Function calls are added to an internal, in-order device queue. However, explicit synchronization can be used to wait until the queue is empty. For example:

The sync statement forces the caller to wait until the two forward transforms are finished.

ArrayFire also does lazy evaluation of some computations. In this case, it stores the order of instructions, but it does not submit work to the device queue until the result is needed. Only then will a kernel be generated and added to the queue. The multiply-by-conjugate statement is an example of lazy evaluation:

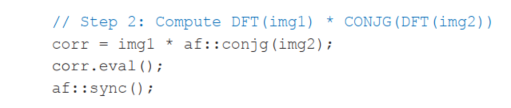
The eval statement forces a kernel to be created and added to the queue. The sync statement forces the caller to wait until the multiply-by-conjugate operation is finished.

Accelerator Offload with oneAPI

Implementing a 1D Fourier correlation using oneAPI has been demonstrated in a previous article and webinar. The principles are the same for the 2D case, so rather than explain each step of the oneAPI implementation, this section will compare the oneAPI and ArrayFire code and highlight differences between these two approaches to heterogeneous parallelism

Initializing the Images on the Device

Data movement between the host CPU and various accelerator devices is an important consideration in heterogeneous parallel programming. If some steps of an algorithm are performed on the host and others on the device, back-and-forth data transfer could limit the performance benefit of accelerator offload. Fortunately, each step of the Fourier correlation algorithm can be done on the device. Once the images are transferred to the device memory, they do not need to be transferred back to the host.

The ArrayFire and SYCL code to initialize the data on the device is shown in Figure 4. The same artificial images from Figure 1 are used for the sake of simplicity. After setting the offload device, the ArrayFire code initializes the data using convenience functions and array syntax (Figure 4, left). Likewise, the oneAPI code initializes a SYCL queue for the default device, allocates sufficient space in the unified shared memory for an in-place, real-to-complex transform, and defines the data layout (Figure 4, right). (Describing the data layout for multidimensional DFTs is beyond the scope of this article, but the FFTW documentation provides a good overview.) The SYCL code performs the initialization on the device by submitting work to the SYCL queue (that is, the parallel_for and single_task kernels). SYCL queues are asynchronous, so these kernels are explicitly told to wait for the work to finish before proceeding.

Figure 4. Initializing the data on the device using ArrayFire (left) and SYCL (right).

The host should not modify the data once it is in the device memory because this will trigger unnecessary host-device transfer. Notice that the image elements are set using a single_task kernel. Without this kernel, the elements would be set on the host, forcing the oneAPI runtime to make the host and device data consistent. This could hurt performance if the data is large (e.g., volumetric images from medical imaging applications).

The ArrayFire code is more compact and intuitive. The oneAPI code is more explicit about where data is allocated and where and when computation is performed. It is also more consistent with FFTW, the popular open-source fast Fourier transform package.

Step 1: Performing the Forward Transforms

Once again, the ArrayFire code is simple and intuitive (Figure 5, left). The function call specifies a 2D real-to-complex (R2C), unnormalized FFT with precision defined by the input data. The oneMKL DFT descriptor approach (Figure 5, right), while not as compact, is familiar to previous MKL DFTI and FFTW users. The oneMKL code initializes a descriptor for a single-precision, real-to-complex transform of the required size and dimensionality, commits this descriptor to the SYCL queue, and then computes the forward transforms. The compute_forward function returns a SYCL event that is used later for synchronization

Figure 5. Performing the forward transforms (real-to-complex) on the device using ArrayFire (left)
and oneMKL (right)

Step 2: Complex Conjugate Multiplication

ArrayFire and oneMKL use different approaches to perform the multiply-by-conjugate operation. ArrayFire uses a straightforward array notation (Figure 6, left). The programmer does not have to specify the device or data layout. oneMKL provides a convenient mulbyconj function (Figure 6, right). The mulbyconj function is more complex, but it gives the programmer explicit control over the data layout and where and when the computation runs (i.e., the SYCL queue and events).

Figure 6. Complex conjugate multiplication using ArrayFire (left) and oneMKL (right).

Step 3: Performing the Backward Transform

The code for steps 1 and 3 is similar except that only a single complex-to-real transform is performed. The ArrayFire code (Figure 7, left) calls fftC2R instead of the fftR2C function. The oneMKL code (Figure 7, right) initializes a new DFT descriptor specifying the complex-to-real data layout.

Figure 7. Performing the backward transforms (complex-to-real) on the device using
ArrayFire (left) and oneMKL (right).

Step 4: MAXLOC Reduction

The SYCL MAXLOC reduction operator used in previous experiments added complexity to the code (see fcorr_1d_usm.cpp). oneDPL provides the same functionality in two functions that will be familiar to C++ programmers: max_element and distance. The MAXLOC reduction shown in Figure 8 (right) uses the oneDPL implementations of these functions. The SYCL queue tells max_element where to perform the computation. It is worth noting that unlike SYCL kernels, oneDPL algorithms are synchronous so there are no explicit wait statements.

The ArrayFire code (Figure 8, left) is not as straightforward as previous steps. The af::flat function flattens the 2D corr array, and then the af::max function finds the maximum correlation score and its location in the flattened array. This location is converted to the x- and y-shift that gives the optimal alignment of the two images, taking into account that ArrayFire is column-major (as noted in Figure 3). The oneDPL code (Figure 8, right) performs similar operations, but must take the oneMKL data layout into account.

Figure 8. Performing the MAXLOC reduction in ArrayFire (left) and oneDPL (right).

Conclusions

The oneAPI and ArrayFire approaches both accomplish the goal of write once, run anywhere heterogeneous parallelism. Performance is not discussed because the entire 2D Fourier correlation computation is done in oneAPI or ArrayFire libraries. The separation of concerns between applications developers and compiler/library developers is a recurring theme in The Parallel Universe. The latter group is primarily concerned with performance and computing efficiency. The former group is primarily concerned with solving a problem as productively as possible. If you’re in this group, you probably prefer high-level programming abstractions that still deliver performance. It’s a reasonable expectation that the libraries will give good performance.

ArrayFire provides a higher level of abstraction, so the ArrayFire Fourier correlation implementation is more concise. Its array notation will be familiar to Fortran, MATLAB, and Python NumPy programmers.

ArrayFire also has a Python API. Lazy evaluation means the runtime controls when computations are launched, but as noted above, programmers can take control if they want to.

The oneAPI implementation is more verbose because it gives the programmer more control over host-device data transfer and where and when computations are performed. The oneMKL DFT descriptors and data layout will be familiar to previous MKL DFTI and FFTW users. In fact, Intel® oneAPI Math Kernel Library supports the FFTW interface. Finally, oneDPL functions will be familiar to C++ programmers.

Ultimately, project requirements and personal preference will guide the choice between oneAPI and ArrayFire.