?gbtrs

Developer Reference for Intel® oneAPI Math Kernel Library for Fortran

Download PDF

ID 766686

Date 12/16/2022

Version

Public

A newer version of this document is available. Customers should click here to go to the newest version.

Visible to Intel only — GUID: GUID-C489B35B-78DE-4C7A-A542-2190CFED44A7

View Details

?gbtrs

Solves a system of linear equations with an LU-factored band coefficient matrix, with multiple right-hand sides.

Syntax

call sgbtrs( trans, n, kl, ku, nrhs, ab, ldab, ipiv, b, ldb, info )

call dgbtrs( trans, n, kl, ku, nrhs, ab, ldab, ipiv, b, ldb, info )

call cgbtrs( trans, n, kl, ku, nrhs, ab, ldab, ipiv, b, ldb, info )

call zgbtrs( trans, n, kl, ku, nrhs, ab, ldab, ipiv, b, ldb, info )

call gbtrs( ab, b, ipiv, [, kl] [, trans] [, info] )

Include Files

mkl.fi, lapack.f90

Description

The routine solves for X the following systems of linear equations:

A*X = B	if `trans`='N',
`A^T*X = B`	if `trans`='T',
`A^H*X = B`	if `trans`='C' (for complex matrices only).

Here A is an LU-factored general band matrix of order n with kl non-zero subdiagonals and ku nonzero superdiagonals. Before calling this routine, call ?gbtrf to compute the LU factorization of A.

Input Parameters

trans	CHARACTER*1. Must be 'N' or 'T' or 'C'.
n	INTEGER. The order of `A`; the number of rows in `B`; `n`≥ 0.
kl	INTEGER. The number of subdiagonals within the band of `A`; `kl`≥ 0.
ku	INTEGER. The number of superdiagonals within the band of `A`; `ku`≥ 0.
nrhs	INTEGER. The number of right-hand sides; `nrhs`≥ 0.
ab, b	REAL for sgbtrs DOUBLE PRECISION for dgbtrs COMPLEX for cgbtrs DOUBLE COMPLEX for zgbtrs. Arrays: `ab(ldab,)`, `b(ldb,)`. The array `ab` contains elements of the LU factors of the matrix `A` as returned by gbtrf. The second dimension of `ab` must be at least `max(1, n)`. The array `b` contains the matrix `B` whose columns are the right-hand sides for the systems of equations. The second dimension of `b` at least `max(1,nrhs)`.
ldab	INTEGER. The leading dimension of the array `ab`; `ldab`≥ 2*`kl` + `ku` +1.
ldb	INTEGER. The leading dimension of `b`; `ldb≥ max(1, n)`.
ipiv	INTEGER. Array, size at least `max(1, n)`. The `ipiv` array, as returned by ?gbtrf.

Output Parameters

Overwritten by the solution matrix X.

info

INTEGER. If info=0, the execution is successful.

If info = -i, the i-th parameter had an illegal value.

LAPACK 95 Interface Notes

Routines in Fortran 95 interface have fewer arguments in the calling sequence than their FORTRAN 77 counterparts. For general conventions applied to skip redundant or reconstructible arguments, see LAPACK 95 Interface Conventions.

Specific details for the routine gbtrs interface are as follows:

ab	Holds the array `A` of size (`2*kl+ku+1,n`).
b	Holds the matrix `B` of size (`n`, `nrhs`).
ipiv	Holds the vector of length min(`m`, `n`).
kl	If omitted, assumed `kl = ku`.
ku	Restored as `lda-2*kl-1`.
trans	Must be 'N', 'C', or 'T'. The default value is 'N'.

Application Notes

For each right-hand side b, the computed solution is the exact solution of a perturbed system of equations (A + E)x = b, where

|E| ≤ c(kl + ku + 1)ε P|L||U|

c(k) is a modest linear function of k, and ε is the machine precision.

If x₀ is the true solution, the computed solution x satisfies this error bound:

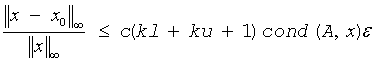
where cond(A,x)= || |A^-1||A| |x| ||_∞ / ||x||_∞≤ ||A^-1||_∞ ||A||_∞ = κ_∞(A).

Note that cond(A,x) can be much smaller than κ_∞(A); the condition number of A^T and A^H might or might not be equal to κ_∞(A).

The approximate number of floating-point operations for one right-hand side vector is 2n(ku + 2kl) for real flavors. The number of operations for complex flavors is 4 times greater. All these estimates assume that kl and ku are much less than min(m,n).

To estimate the condition number κ_∞(A), call ?gbcon.

To refine the solution and estimate the error, call ?gbrfs.

Parent topic: Solving Systems of Linear Equations: LAPACK Computational Routines

Select Your Language

Using Intel.com Search

Quick Links

Recent Searches

Advanced Search

Only search in

Developer Reference for Intel® oneAPI Math Kernel Library for Fortran

?gbtrs

See Also