Developer Reference for Intel® oneAPI Math Kernel Library for C
A newer version of this document is available. Customers should click here to go to the newest version.
Summary Statistics Mathematical Notation and Definitions
The following notations are used in the mathematical definitions and the description of the Intel® oneAPI Math Kernel Library Summary Statistics functions.
Matrix and Weights of Observations
For a random p-dimensional vector ξ = (ξ1,..., ξi,..., ξp), this manual denotes the following:
(X)i=(xij)j=1..n is the result of n independent observations for the i-th component ξi of the vector ξ.
The two-dimensional array X=(xij)n x p is the matrix of observations.
The column [X]j=(xij)i=1..p of the matrix X is the j-th observation of the random vector ξ.
Each observation [X]j is assigned a non-negative weight wj , where
The vector (wj)j=1..n is a vector of weights corresponding to n observations of the random vector ξ.
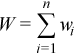
is the accumulated weight corresponding to observations X.
Vector of sample means
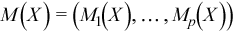with 
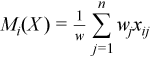
for all i = 1, ..., p.
Vector of sample partial sums
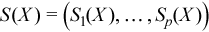with 
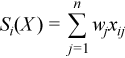
for all i = 1, ..., p.
Vector of sample variances
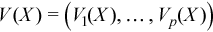with 
, 
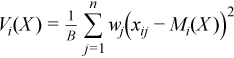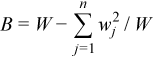
for all i = 1, ..., p.
Vector of sample raw/algebraic moments of k-th order, k≥ 1
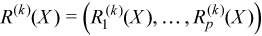with 
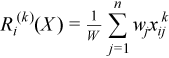
for all i = 1, ..., p.
Vector of sample raw/algebraic partial sums of k-th order, k= 2, 3, 4 (raw/algebraic partial sums of squares/cubes/fourth powers)
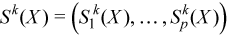with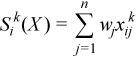 
for all i = 1, ..., p.
Vector of sample central moments of the third and the fourth order
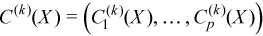with 
, 
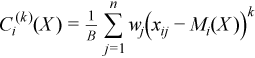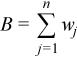
for all i = 1, ..., p and k = 3, 4.
Vector of sample central partial sums of k-th order, k= 2, 3, 4 (central partial sums of squares/cubes/fourth powers)
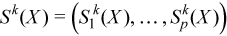with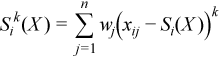 
for all i = 1, ..., p.
Vector of sample excess kurtosis values
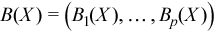with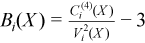 
for all i = 1, ..., p.
Vector of sample skewness values
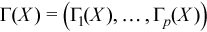with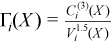 
for all i = 1, ..., p.
Vector of sample variation coefficients
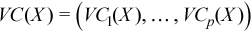with 
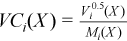
for all i = 1, ..., p.
Matrix of order statistics
Matrix Y = (yij)pxn, in which the i-th row (Y)i = (yij)j=1..n is obtained as a result of sorting in the ascending order of row (X)i = (xij)j=1..n in the original matrix of observations.
Vector of sample minimum values
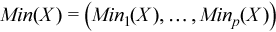, where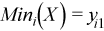 
for all i = 1, ..., p.
Vector of sample maximum values
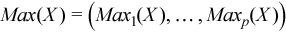, where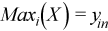 
for all i = 1, ..., p.
Vector of sample median values
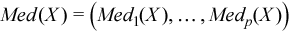, where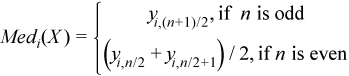 
for all i = 1, ..., p.
Vector of sample median absolute deviations
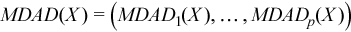, where 
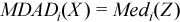with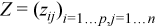 
, 
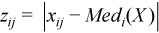
for all i = 1, ..., p.
Vector of sample mean absolute deviations
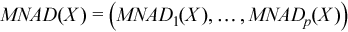, where 
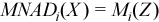with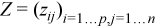 
, 
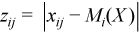
for all i = 1, ..., p.
Vector of sample quantile values
For a positive integer number q and k belonging to the interval [0, q-1], point zi is the k-th q quantile of the random variable ξi if P{ξi≤zi} ≥β and P{ξi≤zi} ≥ 1 - β, where
P is the probability measure.
β = k/n is the quantile order.
The calculation of quantiles is as follows:
j = [(n-1)β] and f = {(n-1)β} as integer and fractional parts of the number (n-1)β, respectively, and the vector of sample quantile values is
Q(X,β) = (Q1(X,β), ..., Qp(X,β))
where
(Qi(X,β) = yi,j+1 + f(yi,j+2 - yi,j+1)
for all i = 1, ..., p.
Variance-covariance matrix
C(X) = (cij(X))p x p
where
, 
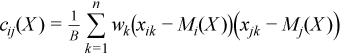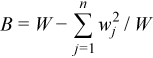
Cross-product matrix (matrix of cross-products and sums of squares)
CP(X) = (cpij(X))p x p
where
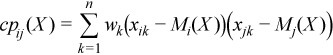
Pooled and group variance-covariance matrices
The set N = {1, ..., n} is partitioned into non-intersecting subsets
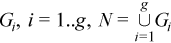
The observation [X]j = (xij)i=1..p belongs to the group r if j∈Gr. One observation belongs to one group only. The group mean and variance-covariance matrices are calculated similarly to the formulas above:
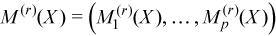with 
, 
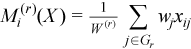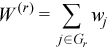
for all i = 1, ..., p,
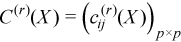
where
, 
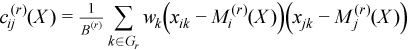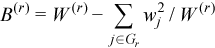
for all i = 1, ..., p and j = 1, ..., p.
A pooled variance-covariance matrix and a pooled mean are computed as weighted mean over group covariance matrices and group means, correspondingly:
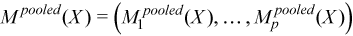with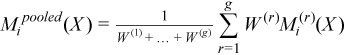 
for all i = 1, ..., p,
, 
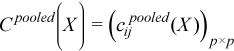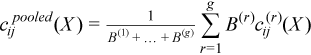
for all i = 1, ..., p and j = 1, ..., p.
Correlation matrix
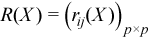, where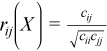 
for all i = 1, ..., p and j = 1, ..., p.
Partial variance-covariance matrix
For a random vector ξ partitioned into two components Z and Y, a variance-covariance matrix C describes the structure of dependencies in the vector ξ:
.
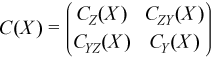The partial covariance matrix P(X) =(pij(X))kxk is defined as
.
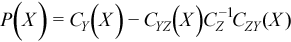where k is the dimension of Y.
Partial correlation matrix
The following is a partial correlation matrix for all i = 1, ..., k and j = 1, ..., k:
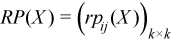, where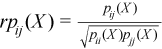 
where
k is the dimension of Y.
pij(X) are elements of the partial variance-covariance matrix.
Sorted dataset
Matrix Y = (yij)pxn, in which the i-th row (Y)i is obtained as a result of sorting in ascending order the row (X)i = (xij)j = 1..n in the original matrix of observations.