A newer version of this document is available. Customers should click here to go to the newest version.
Distributions Template Parameter Method
Method Type |
Distributions |
Math Description |
|---|---|---|
uniform_method::standard uniform_method::accurate |
uniform |
Standard method. Currently there is only one method for these functions. uniform_method::accurate checks for additional s and d data types. For integer data types, it uses d as a BRNG data type (sBRNG data type is used in uniform_method::standard method on GPU). |
gaussian_method::box_muller |
gaussian |
Generates normally distributed random number x thru the pair of uniformly distributed numbers u1 and u2 according to the formula: |
gaussian_method::box_muller2 |
gaussian |
Generates normally distributed random numbers x1 and x2 thru the pair of uniformly distributed numbers u1 and u2 according to the formulas: |
gaussian_method::icdfgeometric_method::icdf |
gaussian geometric |
Inverse cumulative distribution function (ICDF) method. |
exponential_method::icdfexponential_method::icdf_accurate |
exponential |
Inverse cumulative distribution function (ICDF) method. |
weibull_method::icdf weibull_method::icdf_accurate |
weibull |
Inverse cumulative distribution function (ICDF) method. |
cauchy_method::icdf |
cauchy |
Inverse cumulative distribution function (ICDF) method. |
rayleigh_method::icdf rayleigh_method::icdf_accurate |
rayleigh |
Inverse cumulative distribution function (ICDF) method. |
lognormal_method::icdflognormal_method::icdf_accurate |
lognormal |
Inverse cumulative distribution function (ICDF) method. |
lognormal_method::box_muller2lognormal_method::box_muller2_accurate |
lognormal |
Normally distributed random numbers x1 and x2 are produced through the pair of uniformly distributed numbers u1 and u2 according to the formulas: |
gumbel_method::icdf |
gumbel |
Inverse cumulative distribution function (ICDF) method. |
bernoulli_method::icdf |
bernoulli |
Inverse cumulative distribution function (ICDF) method. |
gamma_method::marsagliagamma_method::marsaglia_accurate |
gamma |
For α > 1, a gamma distributed random number is generated as a cube of properly scaled normal random number; for 0.6 ≤α < 1, a gamma distributed random number is generated using rejection from Weibull distribution; for α < 0.6, a gamma distributed random number is obtained using transformation of exponential power distribution; for α = 1, gamma distribution is reduced to exponential distribution. |
beta_method::cja beta_method::cja_accurate |
beta |
Cheng-Johnk-Atkinson method. For min(p, q) > 1, Cheng method is used; for min(p, q) < 1, Johnk method is used, if q + K·p2+ C≤ 0 (K = 0.852..., C=-0.956...) otherwise, Atkinson switching algorithm is used; for max(p, q) < 1, method of Johnk is used; for min(p, q) < 1, max(p, q)> 1, Atkinson switching algorithm is used (CJA stands for Cheng, Johnk, Atkinson); for p = 1or q = 1, inverse cumulative distribution function method is used; for p = 1 and q = 1, beta distribution is reduced to uniform distribution. |
chi_square_method::gamma_based |
chi_square |
(most common): If ν ≥ 17 or ν is odd and 5 ≤ ν ≤ 15, a chi-square distribution is reduced to a Gamma distribution with these parameters: Shape α = ν / 2 Offset a = 0 Scale factor β = 2. The random numbers of the Gamma distribution are generated. |
gaussian_mv_method::box_mullergaussian_mv_method::box_muller2gaussian_mv_method::icdf |
gaussian_mv |
BoxMuller method for multivariate Gaussian distribution. BoxMuller_2 method for multivariate Gaussian distribution. Inverse cumulative distribution function (ICDF) method. |
binomial_method::btpe |
binomial |
Acceptance/rejection method for ntrial·min(p, 1p) ≥ 30 with decomposition into four regions: Two parallelograms Triangle Left exponential tail Right exponenetial tail |
poisson_method::ptpe |
poisson |
Acceptance/rejection method for λ≥ 27 with decomposition into four regions: Two parallelograms Triangle Left exponential tail Right exponenetial tail |
poisson_method::gaussian_icdf_basedpoisson_v_method::gaussian_icdf_based |
poissonpoisson_v |
for λ≥ 1, method based on Poisson inverse CDF approximation by Gaussian inverse CDF; for λ < 1, table lookup method is used. |
hypergeometric_method::h2pe |
hypergeometric |
Acceptance/rejection method for large mode of distribution with decomposition into three regions: Rectangular Left exponential tail Right exponential tail |
negative_binomial_method::nbar |
negative_binomial |
Acceptance/rejection method for: Rectangular (2) trapezoid Left exponential tail Right exponential tail |
multinomial_method::poisson_icdf_based |
multinomial |
Multinomial distribution with parameters m, k, and a probability vector p. Random numbers of the multinomial distribution are generated by Poisson Approximation method. |
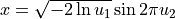
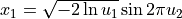
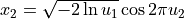Lognormal distribution: generated normally distributed random numbers x1 and x2 are converted to lognormal distribution.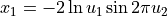
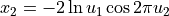Then x1 and x2 are converted to lognormal distribution.
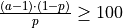with decomposition into five regions: