Developer Reference for Intel® oneAPI Math Kernel Library for C
?feast_sbev/?feast_hbev
Extended Eigensolver interface for standard eigenvalue problem with banded matrices.
Syntax
void sfeast_sbev (const char * uplo, const MKL_INT * n, const MKL_INT * kla, const float * a, const MKL_INT * lda, MKL_INT * fpm, float * epsout, MKL_INT * loop, const float * emin, const float * emax, MKL_INT * m0, float * e, float * x, MKL_INT * m, float * res, MKL_INT * info);
void dfeast_sbev (const char * uplo, const MKL_INT * n, const MKL_INT * kla, const double * a, const MKL_INT * lda, MKL_INT * fpm, double * epsout, MKL_INT * loop, const double * emin, const double * emax, MKL_INT * m0, double * e, double * x, MKL_INT * m, double * res, MKL_INT * info);
void cfeast_hbev (const char * uplo, const MKL_INT * n, const MKL_INT * kla, const MKL_Complex8 * a, const MKL_INT * lda, MKL_INT * fpm, float * epsout, MKL_INT * loop, const float * emin, const float * emax, MKL_INT * m0, float * e, MKL_Complex8 * x, MKL_INT * m, float * res, MKL_INT * info);
void zfeast_hbev (const char * uplo, const MKL_INT * n, const MKL_INT * kla, const MKL_Complex16 * a, const MKL_INT * lda, MKL_INT * fpm, double * epsout, MKL_INT * loop, const double * emin, const double * emax, MKL_INT * m0, double * e, MKL_Complex16 * x, MKL_INT * m, double * res, MKL_INT * info);
Include Files
- mkl.h
Description
The routines compute all the eigenvalues and eigenvectors for standard eigenvalue problems, Ax = λx, within a given search interval.
Input Parameters
- uplo
-
Must be 'U' or 'L' or 'F' .
If uplo = 'U', a stores the upper triangular parts of A.
If uplo = 'L', a stores the lower triangular parts of A.
If uplo= 'F' , a stores the full matrix A.
- n
-
Sets the size of the problem. n > 0.
- kla
-
The number of super- or sub-diagonals within the band in A (kla≥ 0).
- a
-
Array of dimension lda by n, contains either full matrix A or upper or lower triangular part of the matrix A, as specified by uplo
- lda
-
The leading dimension of the array a. Must be at least max(1, n).
- fpm
-
Array, dimension of 128. This array is used to pass various parameters to Extended Eigensolver routines. See Extended Eigensolver Input Parameters for a complete description of the parameters and their default values.
- emin, emax
-
The lower and upper bounds of the interval to be searched for eigenvalues; emin ≤ emax.
NOTE:Users are advised to avoid situations in which eigenvalues nearly coincide with the interval endpoints. This may lead to unpredictable selection or omission of such eigenvalues. Users should instead specify a slightly larger interval than needed and, if required, pick valid eigenvalues and their corresponding eigenvectors for subsequent use. - m0
-
On entry, specifies the initial guess for subspace dimension to be used, 0 < m0≤n. Set m0 ≥ m where m is the total number of eigenvalues located in the interval [emin, emax]. If the initial guess is wrong, Extended Eigensolver routines return info=3.
- x
-
On entry, if fpm[4]=1, the array x of size n by m contains a basis of guess subspace where n is the order of the input matrix.
Output Parameters
- epsout
-
On output, contains the relative error on the trace: |tracei - tracei-1| /max(|emin|, |emax|)
- loop
-
On output, contains the number of refinement loop executed. Ignored on input.
- e
-
Array of length m0. On output, the first m entries of e are eigenvalues found in the interval.
- x
-
On output, the first m columns of x contain the orthonormal eigenvectors corresponding to the computed eigenvalues e, with the i-th column of x holding the eigenvector associated with e[i].
- m
-
The total number of eigenvalues found in the interval [emin, emax]: 0 ≤ m ≤ m0.
- res
-
Array of length m0. On exit, the first m components contain the relative residual vector:
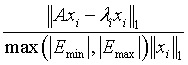
for i=1, 2, …, m, and where m is the total number of eigenvalues found in the search interval.
- info
-
If info=0, the execution is successful. If info ≠ 0, see Output Eigensolver info Details.