Extended Eigensolver Input Parameters

Developer Reference for Intel® oneAPI Math Kernel Library for C

Download PDF

ID 766684

Date 6/30/2025

Version

Public

Extended Eigensolver Input Parameters

The input parameters for Extended Eigensolver routines are contained in an MKL_INT array named fpm. To call the Extended Eigensolver interfaces, this array should be initialized using the routine feastinit.

Parameter	Default	Description
fpm`[0]`	0	Specifies whether Extended Eigensolver routines print runtime status. fpm`[0]`=0 Extended Eigensolver routines do not generate runtime messages at all. fpm`[0]`=1 Extended Eigensolver routines print runtime status to the screen.
fpm`[1]`	8	The number of contour points `N`_e = 8 (see the description of FEAST algorithm). Must be one of {3,4,5,6,8,10,12,16,20,24,32,40,48}.
fpm`[2]`	12	Error trace double precision stopping criteria `ε` (`ε` = 10^-fpm[2]) .
fpm`[3]`	20	Maximum number of Extended Eigensolver refinement loops allowed. If no convergence is reached within fpm`[3]` refinement loops, Extended Eigensolver routines return info=2.
fpm`[4]`	0	User initial subspace. If fpm`[4]`=0 then Extended Eigensolver routines generate initial subspace, if fpm`[4]`=1 the user supplied initial subspace is used.
fpm`[5]`	0	Extended Eigensolver stopping test. fpm`[5]`=0 Extended Eigensolvers are stopped if this residual stopping test is satisfied: generalized eigenvalue problem: standard eigenvalue problem: where `mode` is the total number of eigenvalues found in the search interval and `ε` = 10^-fpm[6] for real and complex or `ε` = 10^-fpm[2] for double precision and double complex. fpm`[5]`=1 Extended Eigensolvers are stopped if this trace stopping test is satisfied: , where `trace`_j denotes the sum of all eigenvalues found in the search interval [emin, emax] at the `j`-th Extended Eigensolver iteration: .
fpm`[6]`	5	Error trace single precision stopping criteria (10^-fpm[6]) .
fpm`[13]`	0	fpm`[13]`=0 Standard use for Extended Eigensolver routines. fpm`[13]`=1 Non-standard use for Extended Eigensolver routines: return the computed eigenvectors subspace after one single contour integration.
fpm`[26]`	0	Specifies whether Extended Eigensolver routines check input matrices (applies to CSR format only). fpm`[26]`=0 Extended Eigensolver routines do not check input matrices. fpm`[26]`=1 Extended Eigensolver routines check input matrices.
fpm`[27]`	0	Check if matrix `B` is positive definite. Set fpm`[27]` `= 1` to check if `B` is positive definite.
fpm`[29]` to fpm`[62]`	-	Reserved for future use.
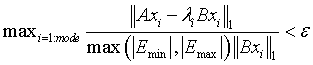
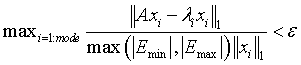
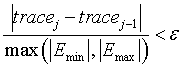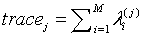fpm`[63]`	0	Use the Intel® oneAPI Math Kernel Library (oneMKL) PARDISO solver with the user-defined PARDISOiparm array settings. NOTE: This option can only be used by Extended Eigensolver Predefined Interfaces for Sparse Matrices. fpm`[63]`=0 Extended Eigensolver routines use the Intel® oneAPI Math Kernel Library (oneMKL) PARDISO defaultiparm settings defined by calling the pardisoinit subroutine. fpm`[63]`=1 The values from fpm`[64]` to fpm`[127]` correspond to `iparm[0]` to `iparm[63]` respectively according to the formula fpm`[64 + i]`= iparm`[i]` for `i` = 0, 1, ..., 63.

Parent topic: Extended Eigensolver Interfaces for Eigenvalues within Interval

Select Your Language

Using Intel.com Search

Quick Links

Recent Searches

Advanced Search

Only search in

Developer Reference for Intel® oneAPI Math Kernel Library for C

Extended Eigensolver Input Parameters