Intel® oneAPI Math Kernel Library Cookbook

Download PDF
ID 758503
Date 11/07/2023
Public
Document Table of Contents
Document Table of Contents x
Intel® oneAPI Math Kernel Library Cookbook
Intel® oneAPI Math Kernel Library Cookbook x
Notices and Disclaimers Getting Technical Support What's New Notational Conventions Related Information Finding an approximate solution to a stationary nonlinear heat equation Factoring general block tridiagonal matrices Solving a system of linear equations with an LU-factored block tridiagonal coefficient matrix Factoring block tridiagonal symmetric positive definite matrices Solving a system of linear equations with a block tridiagonal symmetric positive definite coefficient matrix Computing principal angles between two subspaces Computing principal angles between invariant subspaces of block triangular matrices Evaluating a Fourier integral Using Fast Fourier Transforms for computer tomography image reconstruction Noise filtering in financial market data streams Using the Monte Carlo method for simulating European options pricing Using the Black-Scholes formula for European options pricing Multiple simple random sampling without replacement Using a histospline technique to scale images Speeding up Python* scientific computations Bibliography
Intel® oneAPI Math Kernel Library Cookbook

Solving a system of linear equations with a block tridiagonal symmetric positive definite coefficient matrix

Goal

Solve a system of linear equations with a Cholesky-factored symmetric positive definite block tridiagonal coefficient matrix.

Solution

Given a coefficient symmetric positive definite block tridiagonal matrix (with square blocks each of the same NB-by-NB size) is LLT factored, the solving stage consists of:

  1. Solve the system of linear equations with a lower bidiagonal coefficient matrix which is composed of N by N blocks of size NB by NB and with diagonal blocks which are lower triangular matrices:

    1. Solve the N local systems of equations with lower triangular diagonal blocks of size NB by NB which are used as coefficient matrices and respective parts of the right hand side vectors.

    2. Update the local right hand sides.

  2. Solve the system of linear equations with an upper bidiagonal coefficient matrix which is composted of block size N by N blocks of size NB by NB and with diagonal blocks which are upper triangular matrices.

    1. Solve the local systems of equations.

    2. Update the local right hand sides.

Source code: see the BlockTDS_SPD/source/dpbltrs.f file in the samples archive available at https://www.intel.com/content/dam/develop/external/us/en/documents/mkl-cookbook-samples-120115.zip.

Cholesky factorization of a symmetric positive definite block tridiagonal matrix

      …
      …
      CALL DTRSM('L', 'L', 'N', 'N', NB, NRHS, 1D0, D, LDD, F, LDF)
      DO K = 2, N
          CALL DGEMM('N', 'N', NB, NRHS, NB, -1D0, B(1,(K-2)*NB+1), LDB, F((K-2)*NB+1,1), LDF, 1D0, F((K-1)*NB+1,1), LDF)
          CALL DTRSM('L','L', 'N', 'N', NB, NRHS, 1D0, D(1,(K-1)*NB+1), LDD, F((K-1)*NB+1,1), LDF)
      END DO

      CALL DTRSM('L', 'L', 'T', 'N', NB, NRHS, 1D0, D(1,(N-1)*NB+1), LDD, F((N-1)*NB+1,1), LDF)
      DO K = N-1, 1, -1
          CALL DGEMM('T', 'N', NB, NRHS, NB, -1D0, B(1,(K-1)*NB+1), LDB, F(K*NB+1,1), LDF, 1D0, F((K-1)*NB+1,1), LDF)
          CALL DTRSM('L','L', 'T', 'N', NB, NRHS, 1D0, D(1,(K-1)*NB+1), LDD, F((K-1)*NB+1,1), LDF)
      END DO     
      …

Routines Used

Task

Routine

Description

Solve a local system of linear equations

DTRSM

Solves a triangular matrix equation.

Update the local right hand sides

DGEMM

Computes a matrix-matrix product with general matrices.

Discussion

Consider a system of linear equations described by:


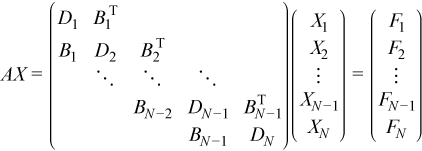
Assume that matrix A is a symmetric positive definite block tridiagonal coefficient matrix with all blocks of size NB by NB. A can be factored as described in Factoring block tridiagonal symmetric positive definite matrices to give:


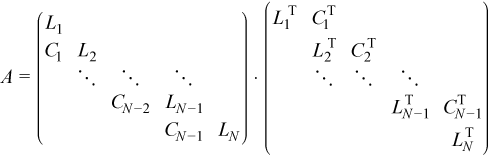
Then the algorithm to solve the system of equations is:

  1. Solve the system of linear equations with a lower bidiagonal coefficient matrix in which the diagonal blocks are lower triangular matrices: 

    Y1=L1-1 F1 //trsm()
do i=2,N
     Gi=Fi - Ci - 1 Yi - 1 //gemm()
     Yi=Li-1 Gi //trsm()
end do

  2. Solve the system of linear equations with an upper bidiagonal coefficient matrix in which the diagonal blocks are upper triangular matrices: 

    XN=LN-T YN //trsm()
do i=N-1,1,-1
     Zi=Fi-CiT Xi + 1 //gemm()
     Xi=Li-T Zi //trsm()
end do
Parent topic: Intel® oneAPI Math Kernel Library Cookbook
Level Two Title