Intel® oneAPI Math Kernel Library Cookbook

Download PDF
ID 758503
Date 11/07/2023
Public
Document Table of Contents
Document Table of Contents x
Intel® oneAPI Math Kernel Library Cookbook
Intel® oneAPI Math Kernel Library Cookbook x
Notices and Disclaimers Getting Technical Support What's New Notational Conventions Related Information Finding an approximate solution to a stationary nonlinear heat equation Factoring general block tridiagonal matrices Solving a system of linear equations with an LU-factored block tridiagonal coefficient matrix Factoring block tridiagonal symmetric positive definite matrices Solving a system of linear equations with a block tridiagonal symmetric positive definite coefficient matrix Computing principal angles between two subspaces Computing principal angles between invariant subspaces of block triangular matrices Evaluating a Fourier integral Using Fast Fourier Transforms for computer tomography image reconstruction Noise filtering in financial market data streams Using the Monte Carlo method for simulating European options pricing Using the Black-Scholes formula for European options pricing Multiple simple random sampling without replacement Using a histospline technique to scale images Speeding up Python* scientific computations Bibliography
Intel® oneAPI Math Kernel Library Cookbook

Factoring block tridiagonal symmetric positive definite matrices

Goal

Perform Cholesky factorization of a symmetric positive definite block tridiagonal matrix.

Solution

To perform Cholesky factorization of a symmetric positive definite block tridiagonal matrix, with N square blocks of size NB by NB:

  1. Perform Cholesky factorization of the first diagonal block.

  2. Repeat N - 1 times moving down along the diagonal:

    1. Compute the off-diagonal block of the triangular factor.

    2. Update the diagonal block with newly computed off-diagonal block.

    3. Perform Cholesky factorization of a diagonal block.

Source code: see the BlockTDS_SPD/source/dpbltrf.f file in the samples archive available at https://www.intel.com/content/dam/develop/external/us/en/documents/mkl-cookbook-samples-120115.zip.

Cholesky factorization of a symmetric positive definite block tridiagonal matrix

      …
      CALL DPOTRF('L', NB, D, LDD, INFO)
      …      
      DO K=1,N-1
          CALL DTRSM('R', 'L', 'T', 'N', NB, NB, 1D0, D(1,(K-1)*NB+1), LDD, B(1,(K-1)*NB+1), LDB)
          CALL DSYRK('L', 'N', NB, NB, -1D0, B(1,(K-1)*NB+1), LDB, 1D0, D(1,K*NB+1), LDD)
          CALL DPOTRF('L', NB, D(1,K*NB+1), LDD, INFO)
          …
      END DO

Routines Used

Task

Routine

Description

Perform Cholesky factorization of diagonal blocks

DPOTRF

Computes the Cholesky factorization of a symmetric (Hermitian) positive-definite matrix.

Compute off-diagonal blocks of the triangular factor

DTRSM

Solves a triangular matrix equation.

Update the diagonal blocks

DSYRK

Performs a symmetric rank-k update.

Discussion

A symmetric positive definite block tridiagonal matrix, with N diagonal blocks Di and N - 1 sub-diagonal blocks Bi of size NB by NB is factored as:


Multiplying the blocks of the matrices on the right gives:


Equating the elements of the original block tridiagonal matrix to the elements of the multiplied factors yields:


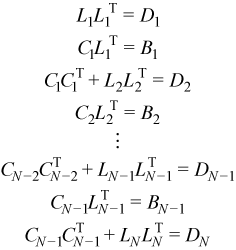
Solving for Ci and LiLiT:


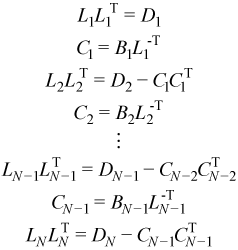
Note that the right-hand sides of the equations for LiLiT is a Cholesky factorization. Therefore a routine chol() for performing Cholesky factorization can be applied to this problem using code such as: 

L1=chol(D1) 
do i=1,N-1
     Ci=Bi∙Li-T //trsm()
     Di + 1:=Di + 1 - Ci∙CiT //syrk()
     Li + 1=chol(Di + 1) 
end do
Parent topic: Intel® oneAPI Math Kernel Library Cookbook
Level Two Title