Intel® oneAPI Math Kernel Library Cookbook

Download PDF
ID 758503
Date 9/27/2021
Public

A newer version of this document is available. Customers should click here to go to the newest version.

Document Table of Contents
Document Table of Contents x
Intel® oneAPI Math Kernel Library Cookbook
Intel® oneAPI Math Kernel Library Cookbook x
Notices and Disclaimers Getting Technical Support What's New Notational Conventions Related Information Finding an approximate solution to a stationary nonlinear heat equation Factoring general block tridiagonal matrices Solving a system of linear equations with an LU-factored block tridiagonal coefficient matrix Factoring block tridiagonal symmetric positive definite matrices Solving a system of linear equations with a block tridiagonal symmetric positive definite coefficient matrix Computing principal angles between two subspaces Computing principal angles between invariant subspaces of block triangular matrices Evaluating a Fourier integral Using Fast Fourier Transforms for computer tomography image reconstruction Noise filtering in financial market data streams Using the Monte Carlo method for simulating European options pricing Using the Black-Scholes formula for European options pricing Multiple simple random sampling without replacement Using a histospline technique to scale images Speeding up Python* scientific computations Bibliography
Intel® oneAPI Math Kernel Library Cookbook

Factoring general block tridiagonal matrices

Goal

Perform LU factorization of a general block tridiagonal matrix.

Solution

oneMKL LAPACK provides a wide range of subroutines for LU factorization of general matrices, including dense matrices, band matrices, and tridiagonal matrices. This recipe extends the range of functionality to general block tridiagonal matrices subject to condition all the blocks are square and have the same order.

To perform LU factorization of a block tridiagonal matrix with square blocks of size NB by NB:

  1. Sequentially apply partial LU factorization to rectangular blocks of size M by N formed by the first two block rows and first three block columns of the matrix (where M = 2NB, N = 3NB, and K = NB), and moving down along the diagonal until the last but one block row is processed.

    Partial LU factorization: for LU factorization of a general block tridiagonal matrix it is useful to have separate functionality for partial LU factorization of a rectangular M-by-N matrix. The partial LU factorization algorithm with parameter K, where K≤ min(M, N), consists of

    1. Perform LU factorization of the M-by-K submatrix.

    2. Solve the system with triangular coefficient matrix.

    3. Update the lower right (M - K)-by-(N - K) block.

    The resulting matrix is A = P(LU + A1) where L is a lower trapezoidal M-by-K matrix, U is an upper trapezoidal matrix, P is permutation (pivoting) matrix, and A1 is a matrix with nonzero elements only in the intersection of the last M - K rows and N - K columns.

  2. Apply general LU factorization to the last (2NB) by (2NB) block.

Source code: see the BlockTDS_GE/source/dgeblttrf.f file in the samples archive available at https://software.intel.com/content/dam/develop/external/us/en/documents/mkl-cookbook-samples-120115.zip.

Performing partial LU factorization

      SUBROUTINE PTLDGETRF(M, N, K, A, LDA, IPIV, INFO)
      …     
          CALL DGETRF( M, K, A, LDA, IPIV, INFO )
          …
          DO I=1,K
              IF(IPIV(I).NE.I)THEN
                  CALL DSWAP(N-K, A(I,K+1), LDA, A(IPIV(I), K+1), LDA)
              END IF
          END DO
          CALL DTRSM('L','L','N','U',K,N-K,1D0, A, LDA, A(1,K+1), LDA)
          CALL DGEMM('N', 'N', M-K, N-K, K, -1D0, A(K+1,1), LDA, 
     &            A(1,K+1), LDA, 1D0, A(K+1,K+1), LDA)
          …

Factoring a block tridiagonal matrix

      …
      DO K=1,N-2
C Form a 2*NB by 3*NB submatrix A with block structure        
C     (D_K   C_K 0    )
C     (B_K D_K+1 C_K+1)         
      …
C Partial factorization of the submatrix
          CALL PTLDGETRF(2*NB, 3*NB, NB, A, 2*NB, IPIV(1,K), INFO)
C Factorization results to be copied back to arrays storing blocks of the tridiagonal matrix
      …
      END DO
C Out of loop factorization of the last 2*NB by 2*NB submatrix 
      CALL DGETRF(2*NB, 2*NB, A, 2*NB, IPIV(1,N-1), INFO)
C Copy the last result back to arrays storing blocks of the tridiagonal matrix
      …

Routines Used

Task

Routine

Description

LU factorization of the M-by-K submatrix

DGETRF

Compute the LU factorization of a general m-by-n matrix

Permute rows of the matrix

DSWAP

Swap two vectors

Solving a system with triangular coefficient matrix

DTRSM

Solve a triangular matrix equation

Update lower-right (M - K)-by-(N - K) block

DGEMM

Compute a matrix-matrix product with general matrices.

Discussion

For partial LU factorization, let A be a rectangular m-by-n matrix:


NOTE:

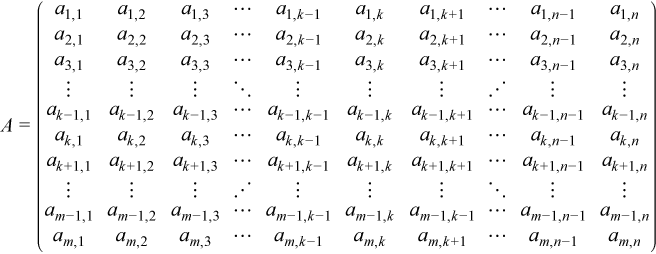
For ease of reading, lower-case indexes such as m, n, k, and nb are used in this discussion. These correspond to the upper-case indexes used in the Fortran solution and code samples.

The matrix can be decomposed using LU factorization of the m-by-k submatrix, where 0 < k≤n. For this application, k< min(m, n), because ?getrf can be used directly to factor the matrix if m≤k≤n or n = k≤m.

A can be represented as a block matrix:


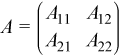
where A11 is a k-by-k submatrix, A12 is a k-by-(n - k) submatrix, A21 is an (m - k)-by-k submatrix, and A22 is an (m - k)-by-(n - k) submatrix.

The m-by-k panel A1 can be defined as


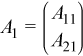
A1 can be LU factored (using ?getrf) as A1 = PLU, where P is a permutation (pivoting) matrix, L is lower trapezoidal with unit elements on the diagonal, and U is upper triangular:



NOTE:

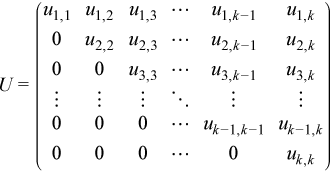
Since the diagonal elements of L do not need to be stored, the array used to store A1 can be used to store the elements of L and U.

Applying PT to the second panel of A gives:


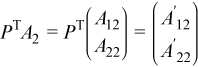
This yields the equation:


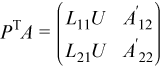
Introducing the term A''12 defined as


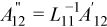
and substituting it into the equation for PTA yields:


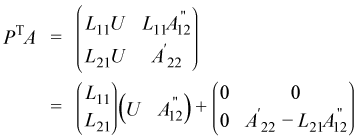
Multiplying the previous equation by P gives:


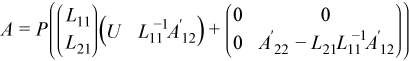
This can be considered a partial LU factorization of the initial matrix.

NOTE:

  • The product L-111A'12 can be computed by calling ?trsm and can be stored in place of the array used for A12. The update A'22 - L21(L-111A'12) can be computed by calling ?gemm and can be stored in place of the array used for A22.

  • If the submatrices do not have full rank, this method cannot be applied because LU factorization would fail.

  • Unlike LU factorization of general matrices, for general block tridiagonal matrices the factorization A = LU described below cannot be written in the form A = PLU (where P is a permutation matrix). Because of pivoting, the structure of the left factor, L, includes permutations. Pivoting also complicates the right factor, U, which has three diagonals instead of two.

For LU factorization of a block tridiagonal matrix, let A be a block tridiagonal matrix where all blocks are square and of the same order nb:


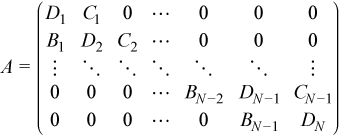
The matrix is to be factored as A = LU.

First, consider 2-by-3 block submatrix


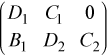
which can be decomposed as


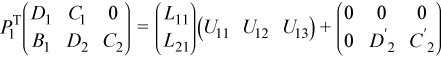
This decomposition can be obtained by applying the partial LU factorization described previously. Here PT1 is a product of nb elementary permutations which can be represented as a 2nb-by-2nb matrix:


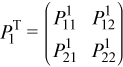
Introducing an N-by-N block matrix where all blocks are size nb-by-nb:


This allows the previous decomposition to be rewritten as:


Next, factor the 2-by-3 block matrix of the second and third rows of the matrix on the right-hand side of that equation:


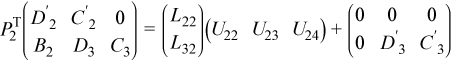
where PT2 is defined as:


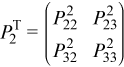
The previous decomposition can be continued as:


Introducing this notation for the pivoting matrix simplifies the equations:



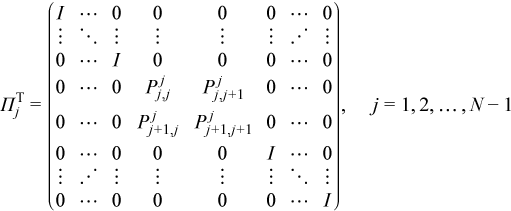
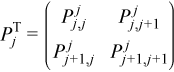
where PTj is 2nb by 2nb, and is located at the intersection of the j-th and (j+1)-st rows and columns. This allows the decomposition above to be written more compactly as


At step N - 2 the local factorization is:


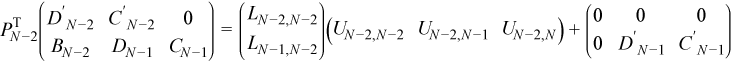
After this step, multiplying by the pivoting matrix:


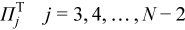
gives:


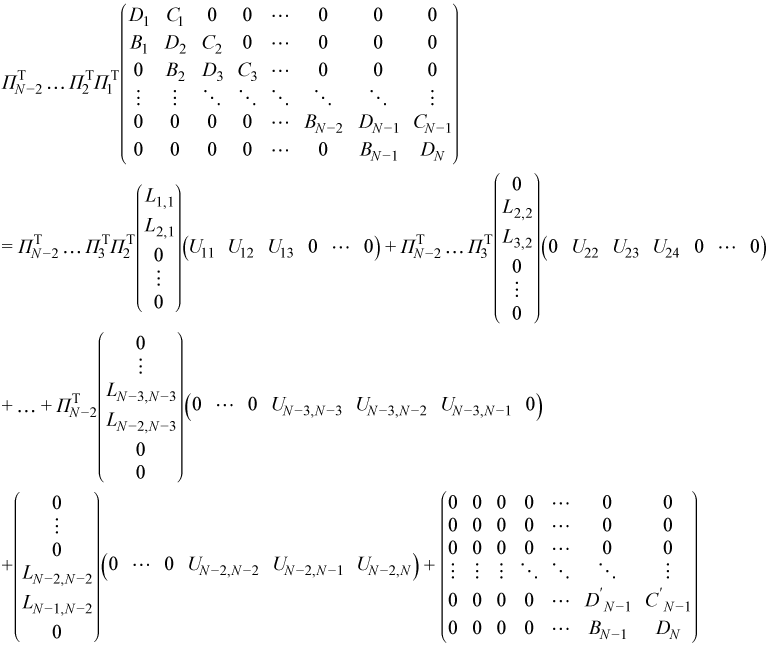
At the last (N - 1)-st step the matrix is square and factorization is complete:


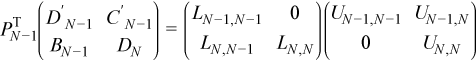
The last step differs from previous ones in the structure of the pivoting as well: all previous PTj for j = 1, 2, ..., N - 2 were products of nb permutations (they depend on nb integer parameters), whereas PTN-1 is applied to a square matrix of order 2nb ( it depends on 2nb parameters). So in order to store all of the pivoting indices an integer array of length (N - 2) nb + 2nb = Nnb is necessary.

Multiplying the previous decomposition from the left by ΠTN-1 gives the final decomposition


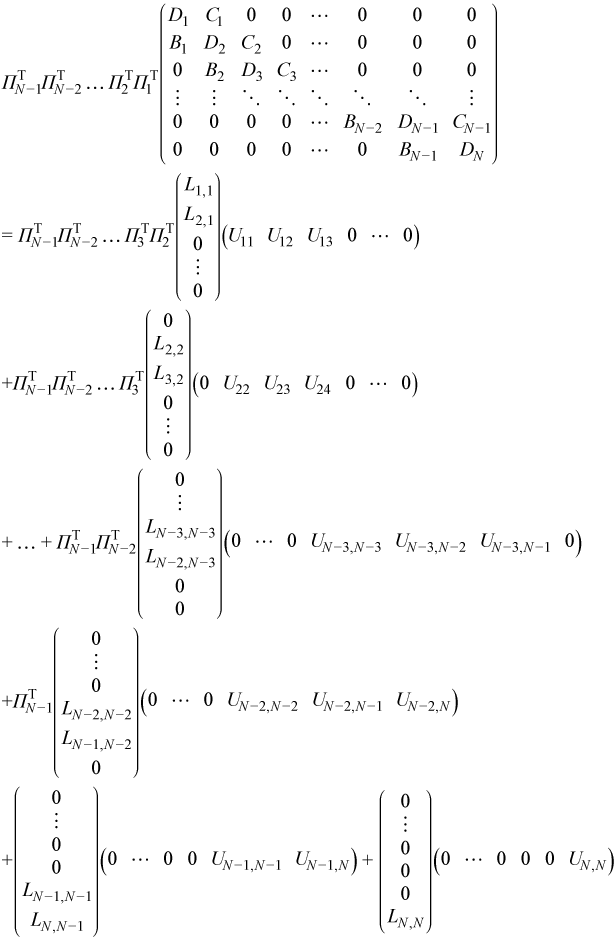
Multiplying this decomposition by Π1Π2...ΠN-1allows it to be written in LU factorization form:


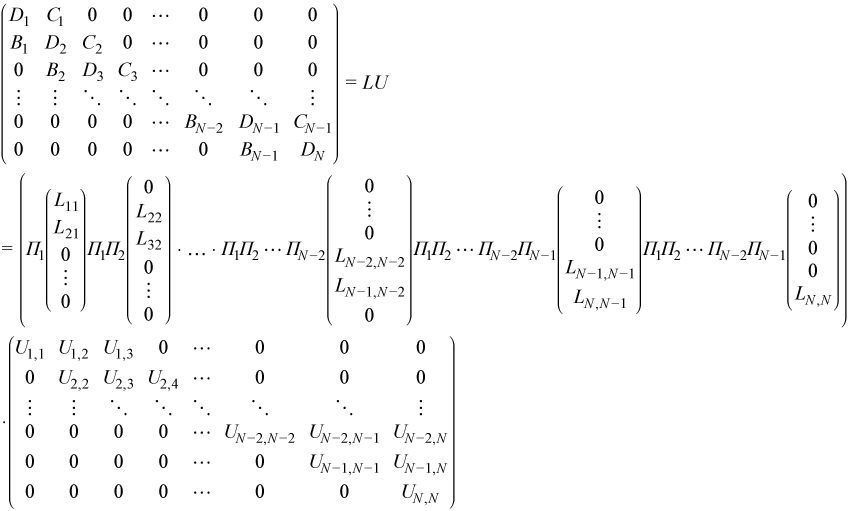
While applying this formula it should be taken into account that Πj for j = 1, 2, …, N-2 are products of nb elementary transpositions applied to block rows with indices j and j+1, but ΠN-1 is the product of 2nb transpositions applied to the last two block rows N-1 and N.

Parent topic: Intel® oneAPI Math Kernel Library Cookbook
Level Two Title