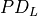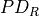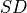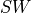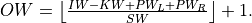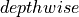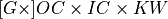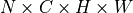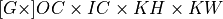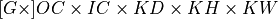Intel® oneAPI Deep Neural Network Developer Guide and Reference
A newer version of this document is available. Customers should click here to go to the newest version.
Convolution
General
The convolution primitive computes forward, backward, or weight update for a batched convolution operation on 1D, 2D, or 3D spatial data with bias.
The convolution operation is defined by the following formulas. We show formulas only for 2D spatial data which are straightforward to generalize to cases of higher and lower dimensions. Variable names follow the standard Naming Conventions.
Let  ,
,  and
and  be
be  ,
,  , and
, and 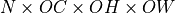 tensors respectively. Let
tensors respectively. Let  be a 1D tensor with
be a 1D tensor with  elements.
elements.
Furthermore, let the remaining convolution parameters be:
Parameter |
Depth |
Height |
Width |
Comment |
|---|---|---|---|---|
Padding: Front, top, and left |
|
|
|
In the API we use padding_l to indicate the corresponding vector of paddings ( _l in the name stands for left ) |
Padding: Back, bottom, and right |
|
|
|
In the API we use padding_r to indicate the corresponding vector of paddings ( _r in the name stands for right ) |
Stride |
|
|
|
Convolution without strides is defined by setting the stride parameters to 1 |
Dilation |
|
|
|
Non-dilated convolution is defined by setting the dilation parameters to 0 |
The following formulas show how oneDNN computes convolutions. They are broken down into several types to simplify the exposition, but in reality the convolution types can be combined.
To further simplify the formulas, we assume that 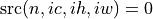 if
if 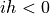 , or
, or  , or
, or 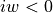 , or
, or  .
.
Forward
Regular Convolution

Here:
Convolution with Groups
In the API, oneDNN adds a separate groups dimension to memory objects representing  tensors and represents weights as
tensors and represents weights as 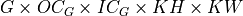 5D tensors for 2D convolutions with groups.
5D tensors for 2D convolutions with groups.
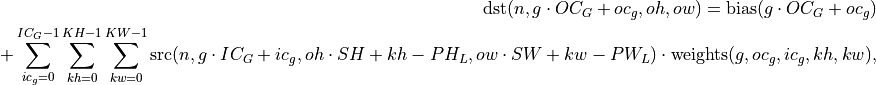
where
 ,
, , and
, and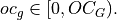
The case when 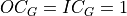 is also known as a depthwise convolution.
is also known as a depthwise convolution.
Convolution with Dilation
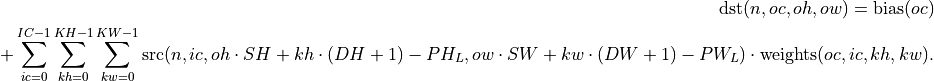
Here:
 where
where 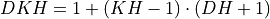 , and
, and where
where 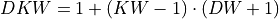 .
.
Deconvolution (Transposed Convolution)
Deconvolutions (also called fractionally strided convolutions or transposed convolutions) work by swapping the forward and backward passes of a convolution. One way to put it is to note that the weights define a convolution, but whether it is a direct convolution or a transposed convolution is determined by how the forward and backward passes are computed.
Difference Between Forward Training and Forward Inference
There is no difference between the dnnl_forward_training and dnnl_forward_inference propagation kinds.
Backward
The backward propagation computes  based on
based on 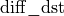 and
and  .
.
The weights update computes  and
and  based on
based on 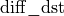 and
and  .
.
 and
and
 might be different on forward propagation, backward propagation, and weights update.
might be different on forward propagation, backward propagation, and weights update.
Execution Arguments
When executed, the inputs and outputs should be mapped to an execution argument index as specified by the following table.
Primitive input/output |
Execution argument index |
|---|---|
|
DNNL_ARG_SRC |
|
DNNL_ARG_WEIGHTS |
|
DNNL_ARG_BIAS |
|
DNNL_ARG_DST |
|
DNNL_ARG_DIFF_SRC |
|
DNNL_ARG_DIFF_WEIGHTS |
|
DNNL_ARG_DIFF_BIAS |
|
DNNL_ARG_DIFF_DST |
|
DNNL_ARG_ATTR_POST_OP_DW |
|
DNNL_ARG_ATTR_MULTIPLE_POST_OP(binary_post_op_position) | DNNL_ARG_SRC_1 |
|
DNNL_ARG_ATTR_MULTIPLE_POST_OP(prelu_post_op_position) | DNNL_ARG_WEIGHTS |
Implementation Details
General Notes
N/A.
Data Types
Convolution primitive supports the following combination of data types for source, destination, and weights memory objects:
Propagation |
Source |
Weights |
Destination |
Bias |
|---|---|---|---|---|
forward |
f32 |
f32 |
f32, u8, s8 |
f32 |
forward |
f16 |
f16 |
f16, f32, u8, s8 |
f16, f32 |
forward |
u8, s8 |
s8 |
u8, s8, s32, f32, f16, bf16 |
u8, s8, s32, f32, f16, bf16 |
forward |
bf16 |
bf16 |
f32, bf16 |
f32, bf16 |
forward |
f8_e5m2 |
f8_e5m2 |
f8_e5m2, f32, f16, bf16 |
f32 |
forward |
f64 |
f64 |
f64 |
f64 |
backward |
f32, bf16 |
bf16 |
bf16 |
|
backward |
f32, f16 |
f16 |
f16 |
|
backward |
f8_e5m2 |
f8_e5m2 |
f8_e5m2 |
|
backward |
f32 |
f32 |
f32 |
f32 |
backward |
f64 |
f64 |
f64 |
f64 |
weights update |
bf16 |
f32, bf16 |
bf16, s8, u8 |
f32, bf16 |
weights update |
f16 |
f32, f16 |
f16 |
f32, f16 |
weights update |
f8_e5m2 |
f32, f8_e5m2 |
f8_e5m2 |
f32 |
Data Representation
Like other CNN primitives, the convolution primitive expects the following tensors:
Spatial |
Source / Destination |
Weights |
|---|---|---|
1D |
|
|
2D |
|
|
3D |
|
|
Physical format of data and weights memory objects is critical for convolution primitive performance. In the oneDNN programming model, convolution is one of the few primitives that support the placeholder memory format tag dnnl::memory::format_tag::any (shortened to any from now on) and can define data and weight memory objects format based on the primitive parameters. When using any it is necessary to first create a convolution primitive descriptor and then query it for the actual data and weight memory objects formats.
While convolution primitives can be created with memory formats specified explicitly, the performance may be suboptimal. The table below shows the combinations of memory formats the convolution primitive is optimized for.
Source / Destination |
Weights |
Limitations |
|---|---|---|
any |
any |
N/A |
any |
N/A |
|
Only on GPUs with Xe-HPC architecture only |
||
any |
Only on CPU |
Post-ops and Attributes
Post-ops and attributes enable you to modify the behavior of the convolution primitive by applying the output scale to the result of the primitive and by chaining certain operations after the primitive. The following attributes and post-ops are supported:
Propagation |
Type |
Operation |
Description |
Restrictions |
|---|---|---|---|---|
forward |
attribute |
Scales the result of convolution by given scale factor(s) |
int8 convolutions only |
|
forward |
attribute |
Sets zero point(s) for the corresponding tensors |
int8 convolutions only |
|
forward |
post-op |
Applies an Eltwise operation to the result |
||
forward |
post-op |
Adds the operation result to the destination tensor instead of overwriting it |
||
forward |
post-op |
Applies a Binary operation to the result |
General binary post-op restrictions |
|
forward |
post-op |
Applies a Convolution operation to the result |
||
forward |
post-op |
Applies an PReLU operation to the result |
The following masks are supported by the primitive:
0, which applies one zero point value to an entire tensor, and
2, which applies a zero point value per each element in a IC or OC dimension for DNNL_ARG_SRC or DNNL_ARG_DST arguments respectively.
When scales and/or zero-points masks are specified, the user must provide the corresponding scales and/or zero-points as additional input memory objects with argument DNNL_ARG_ATTR_SCALES | DNNL_ARG_${MEMORY_INDEX} or DNNL_ARG_ATTR_ZERO_POINTS | DNNL_ARG_${MEMORY_INDEX} during the execution stage. For instance, a source tensor zero points memory argument would be passed with index (DNNL_ARG_ATTR_ZERO_POINTS | DNNL_ARG_SRC).
The library supports any number and order of post operations, but only the following sequences deploy optimized code:
Type of convolutions |
Post-ops sequence supported |
|---|---|
float convolution |
eltwise, sum, sum -> eltwise |
int8 convolution |
eltwise, sum, sum -> eltwise, eltwise -> sum |
The operations during attributes and post-ops applying are done in single precision floating point data type. The conversion to the actual destination data type happens just before the actual storing.
Example 1
Consider the following pseudo-code:
primitive_attr attr;
attr.set_scale(src, mask=0);
attr.set_post_ops({
{ sum={scale=beta} },
{ eltwise={scale=gamma, type=tanh, alpha=ignore, beta=ignored } }
});
convolution_forward(src, weights, dst, attr);The would lead to the following:
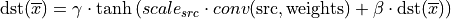
Example 2
The following pseudo-code:
primitive_attr attr;
attr.set_scale(wei, mask=0);
attr.set_post_ops({
{ eltwise={scale=gamma, type=relu, alpha=eta, beta=ignored } },
{ sum={scale=beta} }
});
convolution_forward(src, weights, dst, attr);That would lead to the following:
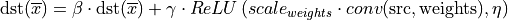
Example 3
The following pseudo-code:
primitive_attr attr;
attr.set_scale(src, mask=0);
attr.set_zero_point(src, mask=0);
attr.set_zero_point(dst, mask=0);
attr.set_post_ops({
{ eltwise={scale=gamma, type=relu, alpha=eta, beta=ignored } }
});
convolution_forward(src, weights, dst, attr);That would lead to the following:
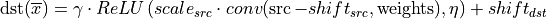
Algorithms
oneDNN implements convolution primitives using several different algorithms:
Direct. The convolution operation is computed directly using SIMD instructions. This is the algorithm used for the most shapes and supports int8, f32, bf16, f16, f8_e5m2, and f64 data types.
Winograd. This algorithm reduces computational complexity of convolution at the expense of accuracy loss and additional memory operations. The implementation is based on the Fast Algorithms for Convolutional Neural Networks by A. Lavin and S. Gray. The Winograd algorithm often results in the best performance, but it is applicable only to particular shapes. Winograd supports GPU (f16 and f32) and AArch64 CPU engines. Winograd does not support threadpool on AArch64 CPU engines.
Implicit GEMM. The convolution operation is reinterpreted in terms of matrix-matrix multiplication by rearranging the source data into a scratchpad memory. This is a fallback algorithm that is dispatched automatically when other implementations are not available. GEMM convolution supports the int8, f32, and bf16 data types.
Direct Algorithm
oneDNN supports the direct convolution algorithm on all supported platforms for the following conditions:
Data and weights memory formats are defined by the convolution primitive (user passes any).
The number of channels per group is a multiple of SIMD width for grouped convolutions.
For each spatial direction padding does not exceed one half of the corresponding dimension of the weights tensor.
Weights tensor width does not exceed 14.
In case any of these constraints are not met, the implementation will silently fall back to an explicit GEMM algorithm.
Winograd Convolution
oneDNN supports the Winograd convolution algorithm on GPU and AArch64 CPU systems. Winograd does not support threadpool on AArch64 CPU systems.
The following side effects should be weighed against the (potential) performance boost achieved from using the Winograd algorithm:
Memory consumption. Winograd implementation in oneDNN requires additional scratchpad memory to store intermediate results. As more convolutions using Winograd are added to the topology, the amount of memory required can grow significantly. This growth can be controlled if the scratchpad memory can be reused across multiple primitives. See Primitive Attributes: Scratchpad for more details.
Accuracy. In some cases Winograd convolution produce results that are significantly less accurate than results from the direct convolution.
Create a Winograd convolution by simply creating a convolution primitive descriptor (step 6 in simple network example specifying the Winograd algorithm. The rest of the steps are exactly the same.
auto conv1_pd = convolution_forward::primitive_desc(engine,
prop_kind::forward_inference, algorithm::convolution_winograd,
conv1_src_md, conv1_weights_md, conv1_bias_md, conv1_dst_md,
conv1_strides, conv1_padding_l, conv1_padding_r);Automatic Algorithm Selection
oneDNN supports dnnl::algorithm::convolution_auto algorithm that instructs the library to automatically select the best algorithm based on the heuristics that take into account tensor shapes and the number of logical processors available. (For automatic selection to work as intended, use the same thread affinity settings when creating the convolution as when executing the convolution.)
Implementation Limitations
Refer to Data Types for limitations related to data types support.
See Winograd Convolution section for limitations of Winograd algorithm implementations.
GPU
Depthwise post-op is not supported
Only reference support is available for f8_e4m3. Optimized implementation is available for f8_e5m2 on Intel(R) Data Center GPU Max Series only.
CPU
Only reference support for fp8 data types (f8_e5m2, f8_e4m3) is is available on CPU.
No support is available for f64.
Performance Tips
Use dnnl::memory::format_tag::any for source, weights, and destinations memory format tags when create a convolution primitive to allow the library to choose the most appropriate memory format.
Example
This C++ API example demonstrates how to create and execute a Convolution primitive in forward propagation mode in two configurations - with and without groups.
Key optimizations included in this example:
Creation of optimized memory format from the primitive descriptor;
Primitive attributes with fused post-ops.