Visible to Intel only — GUID: GUID-35ED9571-066C-4B3B-BBF7-0DF61596CF06
Legal Information
About This Document
About Summary Statistics
Algorithms and Interfaces in Summary Statistics
Common Usage Model of Summary Statistics Algorithms
Processing Data in Blocks
Detecting Outliers in Datasets
Dealing with Missing Observations
Computing Quantiles for Streaming Data
Bibliography
Estimating Raw and Central Moments and Sums, Skewness, Excess Kurtosis, Variation, and Variance-Covariance/Correlation/Cross-Product Matrix
Computing Median Absolute Deviation
Computing Mean Absolute Deviation
Computing Minimum/Maximum Values
Calculating Order Statistics
Estimating Quantiles
Estimating a Pooled/Group Variance-Covariance Matrices/Means
Estimating a Partial Variance-Covariance Matrix
Performing Robust Estimation of a Variance-Covariance Matrix
Detecting Multivariate Outliers
Handling Missing Values in Matrices of Observations
Parameterizing a Correlation Matrix
Sorting an Observation Matrix
Visible to Intel only — GUID: GUID-35ED9571-066C-4B3B-BBF7-0DF61596CF06
Calculating Multiple Estimates
Using Summary Statistics, you can calculate several estimates at a time. In this case, the maximal order of the raw moment required for the computation is defined by the computation method and determines the number of arrays to hold the raw moments. For details, see Computing Estimations for Large Datasets.
To compute a new estimate for the next data portion, you need to allocate, initialize, and pass into the library additional buffers before calling the Compute routine. You can also compute a specific estimate for the next data portion in the environment of a new task.
Summary Statistics provides unbiased estimates for the central moment of the second order and a variance-covariance matrix with standardizing coefficient:
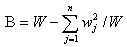
where
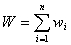
For details, see the Mathematical Notation and Definitions chapter in the Summary Statistics section of [MKLMan].
Before the first call to the Compute routine, you should initialize the elements of the array with zeros or any other values that meet the requirements of the application.
To ensure correct computation of the estimates, you need to pass a pointer to the WA array of two elements:
The first element of the array holds the sum of weights assigned to the observations
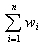
The second element contains the sum of squares of the weights:
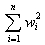
If the whole matrix of observations is available at once and no other data portions are expected, passing a pointer to the WA array is unnecessary.
Estimates of the third and fourth central moments provided by the library are biased and require the sum of weights only, which is the first element of the array described above.
The following example illustrates calculation of the central sum of second order (sums of squares) and a correlation matrix:
#include "mkl_vsl.h"
#define DIM 3 /* dimension of the task */
#define N 1000 /* number of observations */
int main()
{
int i;
VSLSSTaskPtr task;
double x[DIM][N]; /* matrix of observations */
double cor[DIM*(DIM+1)/2], mean[DIM];
double w[2];
MKL_INT p, n, xstorage, corstorage;
int status;
/* Parameters of the task and initialization */
p = DIM;
n = N;
xstorage = VSL_SS_MATRIX_STORAGE_ROWS;
corstorage = VSL_SS_MATRIX_STORAGE_U_PACKED;
w[0] = 0.0; /* sum of weights */
w[1] = 0.0; /* sum of squares of weights */
for ( i = 0; i < p; i++ ) mean[i] = 0.0;
for ( i = 0; i < p*(p+1)/2; i++ ) cor[i] = 0.0;
/* Create a task */
status = vsldSSNewTask( &task, &p, &n, &xstorage, x, 0, 0 );
/* Initialize the task parameters */
status = vsldSSEditTask( task, VSL_SS_ED_ACCUM_WEIGHT, w );
status = vsldSSEditCovCor( task, mean,
NULL, NULL, cor, &corstorage );
/* Compute a correlation matrix */
status = vsldSSCompute( task, VSL_SS_COR, VSL_SS_METHOD_1PASS );
/* Deallocate the task resources */
status = vslSSDeleteTask( &task );
return 0;
}