Developer Reference for Intel® oneAPI Math Kernel Library for C
A newer version of this document is available. Customers should click here to go to the newest version.
?tpmqrt
Applies a real or complex orthogonal matrix obtained from a "triangular-pentagonal" complex block reflector to a general real or complex matrix, which consists of two blocks.
Syntax
lapack_int LAPACKE_stpmqrt (int matrix_layout, char side, char trans, lapack_int m, lapack_int n, lapack_int k, lapack_int l, lapack_int nb, const float* v, lapack_int ldv, const float* t, lapack_int ldt, float* a, lapack_int lda, float* b, lapack_int ldb);
lapack_int LAPACKE_dtpmqrt (int matrix_layout, char side, char trans, lapack_int m, lapack_int n, lapack_int k, lapack_int l, lapack_int nb, const double* v, lapack_int ldv, const double* t, lapack_int ldt, double* a, lapack_int lda, double* b, lapack_int ldb);
lapack_int LAPACKE_ctpmqrt (int matrix_layout, char side, char trans, lapack_int m, lapack_int n, lapack_int k, lapack_int l, lapack_int nb, const lapack_complex_float* v, lapack_int ldv, const lapack_complex_float* t, lapack_int ldt, lapack_complex_float* a, lapack_int lda, lapack_complex_float* b, lapack_int ldb);
lapack_int LAPACKE_ztpmqrt (int matrix_layout, char side, char trans, lapack_int m, lapack_int n, lapack_int k, lapack_int l, lapack_int nb, const lapack_complex_double* v, lapack_int ldv, const lapack_complex_double* t, lapack_int ldt, lapack_complex_double* a, lapack_int lda, lapack_complex_double* b, lapack_int ldb);
Include Files
- mkl.h
Description
The columns of the pentagonal matrix V contain the elementary reflectors H(1), H(2), ..., H(k); V is composed of a rectangular block V1 and a trapezoidal block V2:
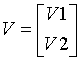
The size of the trapezoidal block V2 is determined by the parameter l, where 0 ≤ l ≤ k. V2 is upper trapezoidal, consisting of the first l rows of a k-by-k upper triangular matrix.
If l=k, V2 is upper triangular;
If l=0, there is no trapezoidal block, so V = V1 is rectangular.
If side = 'L':
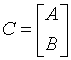
where A is k-by-n, B is m-by-n and V is m-by-k.
If side = 'R':
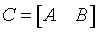
where A is m-by-k, B is m-by-n and V is n-by-k.
The real/complex orthogonal matrix Q is formed from V and T.
If trans='N' and side='L', c contains Q * C on exit.
If trans='T' and side='L', C contains QT * C on exit.
If trans='C' and side='L', C contains QH * C on exit.
If trans='N' and side='R', C contains C * Q on exit.
If trans='T' and side='R', C contains C * QT on exit.
If trans='C' and side='R', C contains C * QH on exit.
Input Parameters
- matrix_layout
-
Specifies whether matrix storage layout is row major (LAPACK_ROW_MAJOR) or column major (LAPACK_COL_MAJOR).
- side
-
='L': apply Q, QT, or QH from the left.
='R': apply Q, QT, or QH from the right.
- trans
-
='N', no transpose, apply Q.
='T', transpose, apply QT.
='C', transpose, apply QH.
- m
-
The number of rows in the matrix B, (m ≥ 0).
- n
-
The number of columns in the matrix B, (n ≥ 0).
- k
-
The number of elementary reflectors whose product defines the matrix Q, (k ≥ 0).
- l
-
The order of the trapezoidal part of V (k ≥ l ≥ 0).
- nb
-
The block size used for the storage of t, k ≥ nb ≥ 1. This must be the same value of nb used to generate t in tpqrt.
- v
-
Size ldv*k for column major layout; ldv*m for row major layout and side = 'L', ldv*n for row major layout and side = 'R'.
The ith column must contain the vector which defines the elementary reflector H(i), for i = 1,2,...,k, as returned by tpqrt in array argument b.
- ldv
-
The leading dimension of the array v.
If side = 'L', ldv must be at least max(1,m) for column major layout and max(1, k for row major layout;
If side = 'R', ldv must be at least max(1,n) for column major layout and max(1, k for row major layout.
- t
-
Array, size ldt*k for column major layout and ldt*nb for row major layout.
The upper triangular factors of the block reflectors as returned by tpqrt
- ldt
-
The leading dimension of the array t. ldt must be at least nb for column major layout and max(1, k for row major layout.
- a
-
If side = 'L', size lda*n for column major layout and lda*k for row major layout ..
If side = 'R', size lda*k for column major layout and lda*m for row major layout ..
The k-by-n or m-by-k matrix A.
- lda
-
The leading dimension of the array a.
If side = 'L', lda must be at least max(1,k) for column major layout and max(1, n for row major layout.
If side = 'R', lda must be at least max(1,m) for column major layout and max(1, k for row major layout.
- b
-
Size ldb*n for column major layout and ldb*m for row major layout.
The m-by-n matrix B.
- ldb
-
The leading dimension of the array b. ldb must be at least max(1,m) for column major layout and max(1, n for row major layout.
Output Parameters
- a
-
Overwritten by the corresponding block of the product Q*C, C*Q, QT*C, C*QT, QH*C, or C*QH.
- b
-
Overwritten by the corresponding block of the product Q*C, C*Q, QT*C, C*QT, QH*C, or C*QH.
Return Values
This function returns a value info.
If info=0, the execution is successful.
If info = -i, the i-th parameter had an illegal value.