Intel® oneAPI Data Analytics Library Developer Guide and Reference
Quality Metrics for Linear Regression
Given a data set 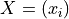 that contains vectors of input variables
that contains vectors of input variables 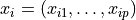 , respective responses
, respective responses 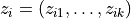 computed at the prediction stage of the linear regression model defined by its coefficients
computed at the prediction stage of the linear regression model defined by its coefficients 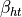 ,
, 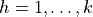 ,
, 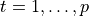 , and expected responses
, and expected responses 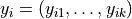 ,
,  , the problem is to evaluate the linear regression model by computing the root mean square error, variance-covariance matrix of beta coefficients, various statistics functions, and so on. See Linear Regression for additional details and notations.
, the problem is to evaluate the linear regression model by computing the root mean square error, variance-covariance matrix of beta coefficients, various statistics functions, and so on. See Linear Regression for additional details and notations.
For linear regressions, the library computes statistics listed in tables below for testing insignificance of beta coefficients and one of the following values of QualityMetricsId:
singleBeta for a single coefficient
groupOfBetas for a group of coefficients
For more details, see [Hastie2009].
Details
The statistics are computed given the following assumptions about the data distribution:
Responses
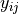 ,
,  , are independent and have a constant variance
, are independent and have a constant variance 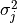 ,
, 
Conditional expectation of responses
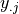 ,
,  , is linear in input variables
, is linear in input variables 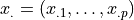
Deviations of
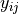 ,
,  , around the mean of expected responses
, around the mean of expected responses 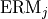 ,
,  , are additive and Gaussian.
, are additive and Gaussian.
Testing Insignificance of a Single Beta
The library uses the following quality metrics:
Quality Metric |
Definition |
|---|---|
Root Mean Square (RMS) Error |
|
Vector of variances |
|
A set of variance-covariance matrices |
|
Z-score statistics used in testing of insignificance of a single coefficient |
|
Confidence interval for |
|
Testing Insignificance of a Group of Betas
The library uses the following quality metrics:
Quality Metric |
Definition |
|---|---|
Mean of expected responses, |
|
Variance of expected responses, |
|
Regression Sum of Squares |
|
Sum of Squares of Residuals |
|
Total Sum of Squares |
|
Determination Coefficient |
|
F-statistics used in testing insignificance of a group of betas |
|
Batch Processing
Testing Insignificance of a Single Beta
Algorithm Input
The quality metric algorithm for linear regression accepts the input described below. Pass the Input ID as a parameter to the methods that provide input for your algorithm. For more details, see Algorithms.
Input ID |
Input |
|---|---|
expectedResponses |
Pointer to the This table can be an object of any class derived from NumericTable. |
model |
Pointer to the model computed at the training stage of the linear regression algorithm. The model can only be an object of the linear_regression::Model class. |
predictedResponses |
Pointer to the This table can be an object of any class derived from NumericTable. |
Algorithm Parameters
The quality metric algorithm for linear regression has the following parameters:
Parameter |
Default Value |
Description |
|---|---|---|
algorithmFPType |
float |
The floating-point type that the algorithm uses for intermediate computations. Can be float or double. |
method |
defaultDense |
Performance-oriented computation method, the only method supported by the algorithm. |
alpha |
0.05 |
Significance level used in the computation of confidence intervals for coefficients of the linear regression model. |
accuracyThreshold |
0.001 |
Values below this threshold are considered equal to it. |
Algorithm Output
The quality metric algorithm for linear regression calculates the result described below. Pass the Result ID as a parameter to the methods that access the results of your algorithm. For more details, see Algorithms.
Result ID |
Result |
|---|---|
rms |
Pointer to the
NOTE:
By default, this result is an object of the HomogenNumericTable class, but you can define the result as an object of any class derived from NumericTable, except for PackedTriangularMatrix, PackedSymmetricMatrix, and CSRNumericTable.
|
variance |
Pointer to the
NOTE:
By default, this result is an object of the HomogenNumericTable class, but you can define the result as an object of any class derived from NumericTable, except for PackedTriangularMatrix, PackedSymmetricMatrix, and CSRNumericTable.
|
betaCovariances |
Pointer to the DataCollection object that contains k numeric tables, each with the The collection can contain objects of any class derived from NumericTable. |
zScore |
Pointer to the
NOTE:
By default, this result is an object of the HomogenNumericTable class, but you can define the result as an object of any class derived from NumericTable, except for PackedTriangularMatrix, PackedSymmetricMatrix, and CSRNumericTable.
|
confidenceIntervals |
Pointer to the
where m is the number of betas in the model (m is equal to p when interceptFlag is set to false at the training stage of the linear regression algorithm; otherwise, m is equal to
NOTE:
By default, this result is an object of the HomogenNumericTable class, but you can define the result as an object of any class derived from NumericTable, except for PackedTriangularMatrix, PackedSymmetricMatrix, and CSRNumericTable.
|
inverseOfXtX |
Pointer to the |
Testing Insignificance of a Group of Betas
Algorithm Input
The quality metric algorithm for linear regression accepts the input described below. Pass the Input ID as a parameter to the methods that provide input for your algorithm. For more details, see Algorithms.
Input ID |
Input |
|---|---|
expectedResponses |
Pointer to the This table can be an object of any class derived from NumericTable. |
predictedResponses |
Pointer to the This table can be an object of any class derived from NumericTable. |
predictedReducedModelResponses |
Pointer to the This table can be an object of any class derived from NumericTable. |
Algorithm Parameters
The quality metric algorithm for linear regression has the following parameters:
Parameter |
Default Value |
Description |
|---|---|---|
algorithmFPType |
float |
The floating-point type that the algorithm uses for intermediate computations. Can be float or double. |
method |
defaultDense |
Performance-oriented computation method, the only method supported by the algorithm. |
numBeta |
0 |
Number of beta coefficients used for prediction. |
numBetaReducedModel |
0 |
Number of beta coefficients ( |
Algorithm Output
The quality metric algorithm for linear regression calculates the result described below. Pass the Result ID as a parameter to the methods that access the results of your algorithm. For more details, see Algorithms.
Result ID |
Result |
|---|---|
expectedMeans |
Pointer to the |
expectedVariance |
Pointer to the |
regSS |
Pointer to the |
resSS |
Pointer to the |
tSS |
Pointer to the |
determinationCoeff |
Pointer to the |
fStatistics |
Pointer to the |
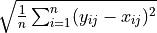 ,
, 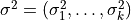
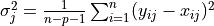 ,
, 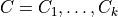 for vectors of betas
for vectors of betas 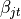 ,
, 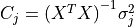 ,
, 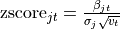 ,
, 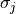 is the j-th element of the vector of variance
is the j-th element of the vector of variance 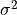 and
and 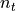 is the t-th diagonal element of the matrix
is the t-th diagonal element of the matrix 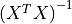
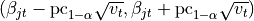 ,
, 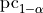 is the
is the 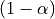 percentile of the Gaussian distribution,
percentile of the Gaussian distribution, 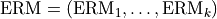
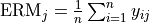 ,
, 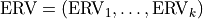
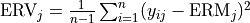 ,
, 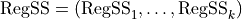
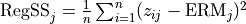 ,
, 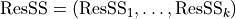
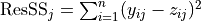 ,
, 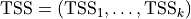
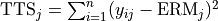 ,
, 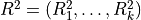
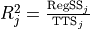 ,
, 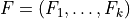
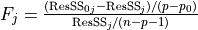 ,
, 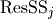 are computed for a model with
are computed for a model with 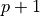 betas and
betas and 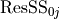 are computed for a reduced model with
are computed for a reduced model with 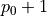 betas (
betas (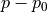 betas are set to zero)
betas are set to zero)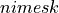 numeric table with responses (k dependent variables) used for training the linear regression model.
numeric table with responses (k dependent variables) used for training the linear regression model. numeric table that contains root mean square errors computed for each response (dependent variable)
numeric table that contains root mean square errors computed for each response (dependent variable)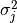 ,
, 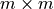 variance-covariance matrix for betas of the j-th response (dependent variable), where m is the number of betas in the model (m is equal to p when interceptFlag is set to false at the training stage of the linear regression algorithm; otherwise, m is equal to p + 1 ).
variance-covariance matrix for betas of the j-th response (dependent variable), where m is the number of betas in the model (m is equal to p when interceptFlag is set to false at the training stage of the linear regression algorithm; otherwise, m is equal to p + 1 ). numeric table that contains the Z-score statistics used in the testing of insignificance of individual linear regression coefficients, where m is the number of betas in the model (m is equal to p when interceptFlag is set to false at the training stage of the linear regression algorithm; otherwise, m is equal to
numeric table that contains the Z-score statistics used in the testing of insignificance of individual linear regression coefficients, where m is the number of betas in the model (m is equal to p when interceptFlag is set to false at the training stage of the linear regression algorithm; otherwise, m is equal to 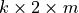 numeric table that contains limits of the confidence intervals for linear regression coefficients:
numeric table that contains limits of the confidence intervals for linear regression coefficients: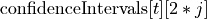 is the left limit of the confidence interval computed for the j-th beta of the t-th response (dependent variable)
is the left limit of the confidence interval computed for the j-th beta of the t-th response (dependent variable)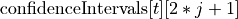 is the right limit of the confidence interval computed for the j-th beta of the t-th response (dependent variable),
is the right limit of the confidence interval computed for the j-th beta of the t-th response (dependent variable),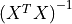 matrix, where m is the number of betas in the model (m is equal to p when interceptFlag is set to false at the training stage of the linear regression algorithm; otherwise, m is equal to
matrix, where m is the number of betas in the model (m is equal to p when interceptFlag is set to false at the training stage of the linear regression algorithm; otherwise, m is equal to 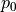 ) used for prediction with the reduced linear regression model, where
) used for prediction with the reduced linear regression model, where