Single Instruction Multiple Data Made Easy with Intel® Implicit SPMD Program Compiler

What are the best ways to vectorize game code, to access the power of Intel^® Streaming SIMD Extensions (Intel^® SSE) vector units across the broadest range of popular and emerging CPUs?

Traditionally, SIMD (single instruction, multiple data) code is written with hand-coded intrinsics or generated by an auto-vectorizing compiler. Targeting multiple families of SIMD intrinsics in your game can add a lot of development time.

Auto-vectorizing compilers have tried to ease the burden of writing code against multiple instruction sets, but often leave performance lacking.

There are trade-offs to both approaches. But if you want easy and portable code, with a low barrier of entry and improved productivity, use Intel^® Implicit SPMD Program Compiler (Intel^® ISPC).

Why SIMD

SIMD boosts CPU performance by applying the same operations across multiple data lanes. More lanes usually mean better performance—as long as the code aligns with the processor’s instruction set.

Game developers typically vectorize their code for the most widely available SIMD instruction set. As a result, instruction sets such as Intel^® Streaming SIMD Extensions 4 (Intel^® SSE4) garner the lion’s share of support. Meanwhile, newer sets such as Intel^® Advanced Vector Extensions 2 (Intel^® AVX2) and Intel^® Advanced Vector Extensions 512 (Intel^® AVX-512) are comparatively untapped. In some cases, hardcore gamers and early adopters may wonder why their state-of-the-art CPU hasn’t delivered the performance boost they expected.

It is likely that developers do not code for every available SIMD set because of the high productivity cost of targeting multiple ISAs (instruction set architectures). To make things more complicated, different versions of a processor within a processor family might offer different SIMD instruction sets. Writing intrinsic code for every instruction set is simply impractical.

Current Methods

SIMD programming techniques are applied at compile-time or link-time. These techniques include:

• Compiler-based auto-vectorization
• Calls to vector-class libraries
• Hand-coded intrinsics
• Inline assembly

Each approach has its pros and cons. Hand-coded intrinsics—when handled by an intrinsics ninja—typically deliver excellent results. But hand-coding for a wide range of SIMD instruction sets can increase complexity, is time-consuming, and increases maintenance costs. For example, if you want to target multiple ISAs, you need to write multiple algorithms. This decreases productivity and increases code complexity.

Auto-vectorizing compilers can reduce the complexity of targeting multiple ISAs, but they are far from perfect. The compiler is no substitute for an experienced programmer. The programmer is often left to optimize manually, using SIMD intrinsics or inline assembly.

Enter Intel ISPC®

Intel ISPC is a C-like language with new keywords that make vectorization straightforward. It abstracts the width of the SIMD registers, and the programmer need only write the program for one instance. The compiler then parallelizes the execution across the SIMD units.

Intel ISPC has a rich standard library for math, bit manipulation, memory, and cross-lane operations. It’s relatively easy to include in C/C++ applications: simply include a generated header and link the resulting object files.

Essentially, Intel ISPC will explicitly vectorize your code to optimize it for various SIMD instruction sets on x86 (32 bit and 64 bit) and 64 bit ARM CPUs. It uses an SPMD (single program, multiple data) execution model that runs a number of program instances in parallel.

Intel ISPC is available on GitHub* and runs on Windows*, Mac* OS X*, and Linux* operating systems.

Testing One, Two, Three

We compared the programmer-hours spent writing intrinsics in C++ for multiple ISAs to those spent on write-once Intel ISPC code for the same algorithm. Our hypothesis was that Intel ISPC would beat a novice SIMD developer in both programmer-hours and performance. 

Tests compared the performance of:

• Scalar C++ code
• Auto-vectorized C++ code (Microsoft* C/C++ Optimizing Compiler Version 19.15.26726)
• Manually vectorized C++ code
• Explicitly vectorized Intel ISPC code

The test platform consisted of:

• CPU: Intel^® Core™ i9-9780XE
• SIMD support: Intel SSE2, Intel AVX, Intel AVX2 and Intel AVX-512
• Memory: 32 GB RAM
• Operating system: Windows^® 10 Pro (64-bit)

Shoelace Formula Workload

We used a triangle culling algorithm called the shoelace formula as a test workload. The shoelace formula computes the area of triangles. Its name comes from the criss-cross pattern used to multiply the X-Y coordinates of a triangle’s vertices. Each vertex has two components, X and Y. The sign of the area determines whether the triangle faces front or back, based on the winding order. This can be used to determine which triangles need to be culled.

Figure 1. The criss-cross, shoelace-style pattern illustrates how the area of a triangle is calculated by the shoelace formula.

Test Cases

We used the test cases with the shoelace formula triangle-culling algorithm, as shown in Figure 2, to determine whether a triangle faces forward or backward.

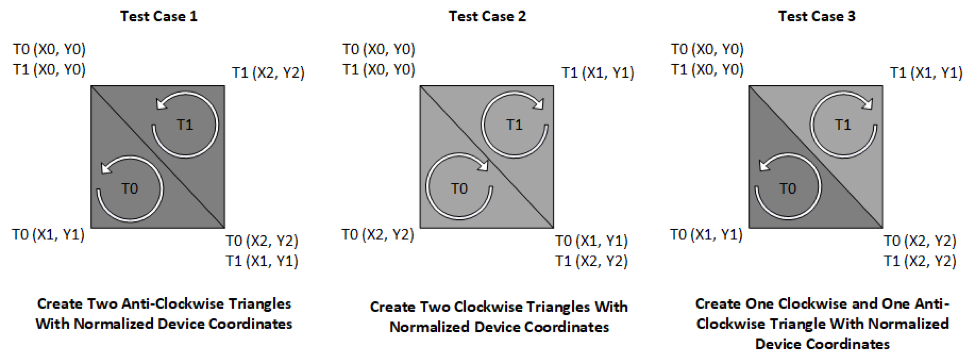
Figure 2. Test cases with the shoelace formula triangle-culling algorithm.

Test Case 1 used one million counterclockwise triangles that were not culled by our algorithm. Test Case 2 used one million clockwise triangles that were culled by our algorithm. Test Case 3 used half a million counterclockwise triangles and half a million clockwise triangles, of which 50% were culled.

Data Layout Optimization

Our naïve approach assumed that we could fit all three vertices of a triangle into two Intel SSE SIMD registers. This approach worked, but the fourth lane duplicated the first.

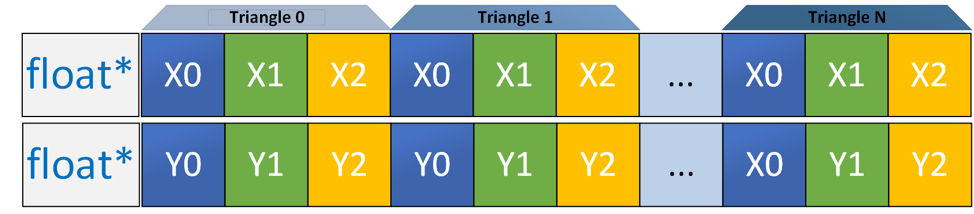
Figure 3. Array of structures (AoS) data layout: vertex components from each triangle are interleaved in an array.

We realized we had fallen into one of the classic pitfalls of SIMD programming: We had chosen a data layout that didn’t fully utilize our SIMD registers. We were only using three-quarters of the lanes available in SSE.

Figure 4. AoS Data Layout loaded into two Intel^® SSE registers. Notice Lane 3 is a duplicate of Lane 0.

The approach shown in Figure 3 worked with the shoelace algorithm, but required an extra load operation to fill Lane 3 with the data from Lane 0. Additionally, we were able to operate on only one triangle at a time in our Intel SSE registers.

Figure 5. Code showing our per-triangle data layout.

// Naïve Approach (Structure of Arrays of Structures)
struct alignas(16) Mesh
{
    // Per-Triangle X-Components
    // [t0x0][t0x1][t0x2] ... [tNx0][tNx1][tNx2]
    float* x;
    // Per-Triangle Y-Components
    // [t0y0][t0y1][t0y2] ... [tNy0][tNy1][tNy2]
    float* y;
};

Our first attempt resulted in a bottleneck. We determined that we could transpose the data using additional SIMD registers. This eliminated the need to duplicate a vertex in Lane 3 of the SIMD register.

We reorganized our data into a Struct of Arrays (SoA) layout that allowed us to fully utilize our SIMD lanes.

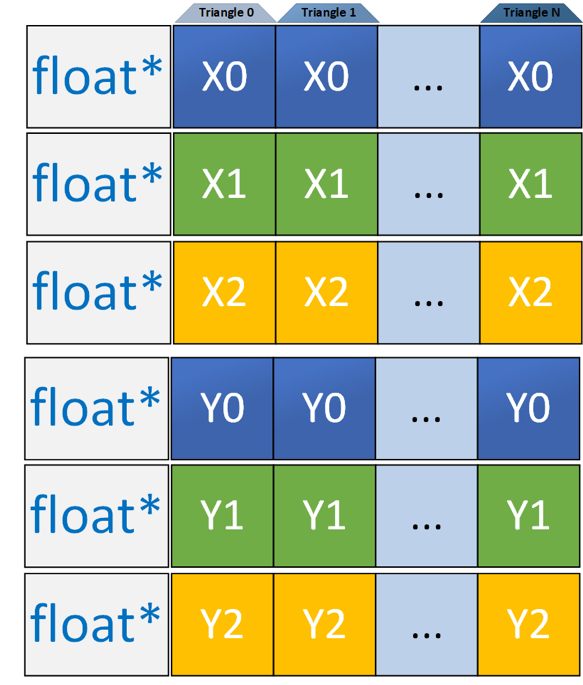
Figure 6. SoA data layout: vertex components from each triangle are transposed into unique arrays.

Using the SoA layout with the Intel SSE instruction set, you can process four triangles concurrently. There is no need for the additional load of duplicated Lane 0 data.

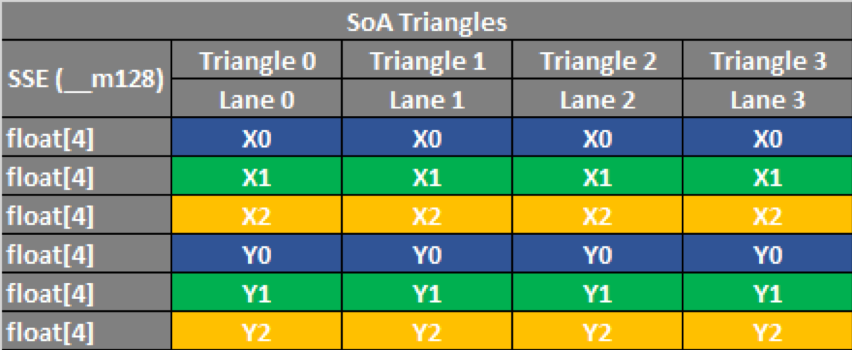
Figure 7. SoA data layout loaded into six SSE registers. Note that four triangles can be computed concurrently.

Our transposed approach required four additional SSE registers. However, as you can see, Lane 3 is no longer a duplicate, and we can compute four triangles concurrently with the same size registers as our AoS layout.

Figure 8. Code sample showing our SoA per-vertex data layout.

// Optimized Approach (Struct of Arrays)
struct alignas(16) MeshSoA
{
    // Per-Vertex X-Components
    // [t0x0][t1x0][t2x0][t3x0] ... [tNx0]
    // [t0x1][t1x1][t2x1][t3x1] ... [tNx1]
    // [t0x2][t1x2][t2x2][t3x2] ... [tNx2]
    float *x0, *x1, *x2;
 
    // Per-Vertex Y-Components
    // [t0y0][t1y0][t2y0][t3y0] ... [tNy0]
    // [t0y1][t1y1][t2y1][t3y1] ... [tNy1]
    // [t0y2][t1y2][t2y2][t3y2] ... [tNy2]
    float *y0, *y1, *y2;
};

Running Intel AVX2 with 256-bit registers would allow us to expand to eight triangles. Intel AVX-512 would process 16 triangles concurrently. Our conclusion: optimizing data layout results in a huge, portable performance gain.

Data Translation

In a large code base, refactoring the data layout of a core data structure is often challenging. It requires significant developer time and regression testing. However, using SIMD, you can translate your data in memory before calculation. This can impact performance, because you need to call additional SIMD instructions, but it reduces refactoring time.

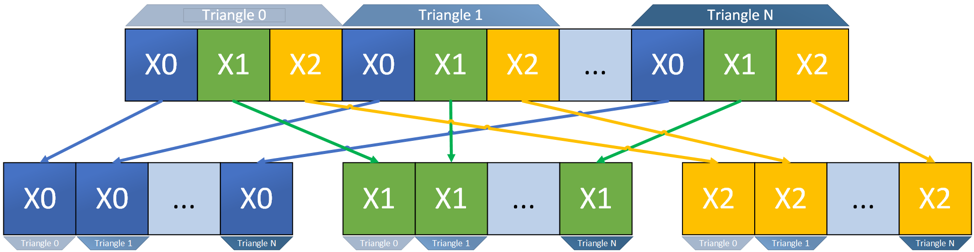
Figure 9. Conceptual diagram of in-memory data layout translation.

The built-in functions of Intel ISPC make this easy. It’s as simple as calling aos_to_soa3 with your starting memory location. This loads it into three varying float variables, representing the X and Y components of each triangle’s vertices.

Figure 10. Code sample showing the function call aos_to_sao3. This is used to translate data layouts in memory using Intel^® ISPC.

// Load X Values 
varying float x0, x1, x2;
aos_to_soa3(&xx[3*i], &x0, &x1, &x2);

// Load Y Values
varying float y0, y1, y2;
aos_to_soa3(&yy[3*i], &y0, &y1, &y2);

Porting Scalar C++ to Intel® ISPC

A novice or intermediate software developer may need several attempts to write well optimized SIMD code. However, translating our scalar implementation to Intel^® ISPC took less than an hour and was straightforward. More complex algorithms may take longer to port, but nowhere near as long as writing all of the hand-coded intrinsics yourself.

Figure 11. A line-by-line comparison of C++ scalar code and Intel ISPC vector code.

void CPP_Scalar_SoA(
    float const* const x0,
    float const* const x1,
    float const* const x2,
    float const* const y0,
    float const* const y1,
    float const* const y2,
    int cullMode,
    int &trisCulled
)
{
    trisCulled = 0;

    // Loop Through Triangles
    for ( int i = 0; i < 1000000; i++ )
    {    
        // First Shift & Multiply
        float v0m0 = x0[i] * y1[i];
        float v1m0 = x1[i] * y2[i];
        float v2m0 = x2[i] * y0[i];

        // Second Shift & Multiply
        float v0m1 = x1[i] * y0[i];
        float v1m1 = x2[i] * y1[i];
        float v2m1 = x0[i] * y2[i];

        // Subtract for Differences
        float v0s0 = v0m0 - v0m1;
        float v1s0 = v1m0 - v1m1;
        float v2s0 = v2m0 - v2m1;

        // Sum for Area
        float area = v0s0 + v1s0 + v2s0;

        if (( cullMode == BACK_CW
             || cullMode == FRONT_CCW)
            && area < 0.0f)
        {
             trisCulled++;
        }
        else if  (( cullMode == FRONT_CW
                     || cullMode == BACK_CCW)
                    && area > 0.0f)
        {
            trisCulled++;
        }
    }
}

void ISPC_AVX_SoA(
    uniform float const* uniform const x0,
    uniform float const* uniform const x1,
    uniform float const* uniform const x2,
    uniform float const* uniform const y0,
    uniform float const* uniform const y1,
    uniform float const* uniform const y2,
    uniform int cullMode,
    uniform int &trisCulled,
)
{
    trisCulled = 0;

     // Loop Through Triangles
    foreach ( i=0 ... 1000000 )
    {
        // First Shift & Multiply
        varying float v0m0 = x0[i] * y1[i];
        varying float v1m0 = x1[i] * y2[i];
        varying float v2m0 = x2[i] * y0[i];

        // Second Shift & Multiply
        varying float v0m1 = x1[i] * y0[i];
        varying float v1m1 = x2[i] * y1[i];
        varying float v2m1 = x0[i] * y2[i];

        // Subtract for Differences
        varying float v0s0 = v0m0 - v0m1;
        varying float v1s0 = v1m0 - v1m1;
        varying float v2s0 = v2m0 - v2m1;

        // Sum for Area
        varying float area = v0s0 + v1s0 + v2s0;

        if  (( cullMode == BACK_CW
              || cullMode == FRONT_CCW))
        {
            varying int test = area < 0.0f;
            trisCulled += reduce_add( test );
        }
        else if (( cullMode == FRONT_CW
                    || cullMode == BACK_CCW))
        {
            varying int test = area > 0.0f;
            trisCulled += reduce_add( test );
        }
    }
}

As you can see in the code comparison above, the function signature was modified to add uniform keywords. Instead of a for loop, we used the foreach keyword offered by Intel^® ISPC and iterated over the same range with a slightly modified loop syntax. Variables in the loop body use the varying keyword. This can be used implicitly but is shown here for clarity. Uniform variables represent scalar values, and varying variables represent a vector, with the number of lanes defined by programCount.

Compare the above Intel^® ISPC implementation with our hand-optimized AVX code, below.

Figure 12. Our hand-optimized AVX code.

void Manual_AVX_SoA(
    float const*const x0,
    float const*const x1,
    float const*const x2,
    float const*const y0,
    float const*const y1,
    float const*const y2,
    int cullMode,
    int &trisCulled
)
{
    int i;
    trisCulled = 0;
 
    // Loop Through 8 Triangles Per Pass
    for (i = 0; i < 1000000; i += 8)
   { 
        // Load Per-Triangle X-Components
        const __m256 i0x0 = _mm256_load_ps(x0 + i);
        const __m256 i1x1 = _mm256_load_ps(x1 + i);
        const __m256 i2x2 = _mm256_load_ps(x2 + i);

        // Load Per-Triangle Y-Components
        const __m256 i3y0 = _mm256_load_ps(y0 + i);
        const __m256 i4y1 = _mm256_load_ps(y1 + i);
        const __m256 i5y2 = _mm256_load_ps(y2 + i);
 
        // First Shift & Multiply
        const __m256 m0g0 = _mm256_mul_ps(i0x0, i4y1);
        const __m256 m0g1 = _mm256_mul_ps(i1x1, i5y2);
        const __m256 m0g2 = _mm256_mul_ps(i2x2, i3y0);

        // Second Shift & Multiply
        const __m256 m1g0 = _mm256_mul_ps(i1x1, i3y0);
        const __m256 m1g1 = _mm256_mul_ps(i2x2, i4y1);
        const __m256 m1g2 = _mm256_mul_ps(i0x0, i5y2);
 
        // Subtract for Differences
        const __m256 d0 = _mm256_sub_ps(m0g0, m1g0);
        const __m256 d1 = _mm256_sub_ps(m0g1, m1g1);
        const __m256 d2 = _mm256_sub_ps(m0g2, m1g2);
 
        // Sum for Area
        const __m256 s = _mm256_add_ps(_mm256_add_ps(d0, d1), d2);

        // Create a comparison mask 
        const __m256 m = _mm256_setzero_ps();

        // compare the values against 0 - result will be 0xffffffff or 0
        const __m256 test = _mm256_cmp_ps(s, m, _CMP_NLE_US);
        const __m256i test_int = _mm256_cvtps_epi32(test);  // convert the result to an integer
  
        // set the max to 1
        const __m256i one = _mm256_set1_epi32(1);
 
         // compute the min between 0xffffffff/0x0 stored in test_int and 1
        const __m256i max = _mm256_min_epu32(one, test_int);
 
         // horizontally add the values to get the result in element 0
         // adds elements 0 & 1, and 2 & 3 and stores them in elements 0, 1
        __m256i sum = _mm256_hadd_epi32(max, max);          	
        
        // adds elements 0 and 1, the total should now be in element 0
        sum = _mm256_hadd_epi32(sum, sum);           

        // adds elements 0 and 1, the total should now be in element 0
        sum = _mm256_hadd_epi32(sum, sum);  

        // extract the total from element zero
        int total = _mm256_extract_epi32(sum, 0);
 
        if (cullMode == BACK_CW || cullMode == FRONT_CCW)
        {
            trisCulled += (8 - total);
        }
        else if (cullMode == FRONT_CW || cullMode == BACK_CCW)
        {
             trisCulled += total;
         }
    }
}

As you can see, operations that compare whether the area is greater than or less than zero introduce complexity. Meanwhile, readability is reduced when compared to the original scalar implementation.

SIMD Width/Workload Performance

Measuring our test cases showed that the Intel ISPC code performed just as well as our hand-optimized C++. However, the Intel ISPC code was much easier to write.

Both proved faster than the naïvely enabled auto-vectorization code. Auto-vectorization might improve with additional analysis and optimization. However, such iterations would require more development than was necessary to calculate our Intel ISPC performance results.

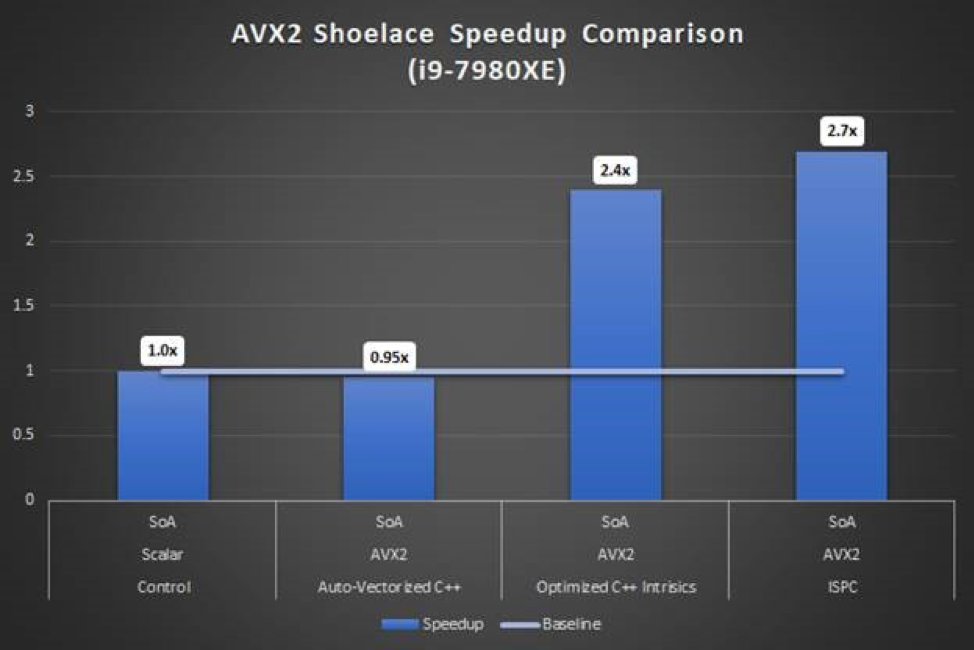
Figure 13. Performance data shows Intel^® ISPC has near identical performance to hand-coded intrinsics. Both are faster than naïvely enabled auto-vectorization.

Our test algorithm was memory-bound. Nonetheless, even in a memory-bound application, Intel ISPC and/or hand-optimized C++ are faster than scalar or naïve enabling of auto-vectorization.

Conclusion

It takes significant time and effort to learn an instruction set, and its corresponding compiler intrinsics. For programmers new to writing intrinsics, achieving working and efficient code is time-consuming. And once an algorithm or system is coded in intrinsics, further effort is required to port it to another instruction set.

However, we spent several hours writing tests for the various SIMD ISAs in C++ intrinsics, and were able to write these tests in Intel^® ISPC in a matter of hours. Creating subsequent tests for different ISAs was as easy as changing a command line option.

Our testing demonstrated that, for this algorithm, Intel ISPC-generated code performance is on par with hand-coded compiler intrinsics. We also learned that Intel ISPC code is significantly easier to read than C++ intrinsics. In terms of readability, portability, performance, and time savings for new code it pays to spend a short while learning a new language: Intel ISPC.

Appendix: Machine Configuration

• Processor: Intel Core™ i9-7980XE CPU @ 2.60 GHz (36 CPUs), ~2.6 GHz 
• Operating System: Windows 10 Pro 64-bit (10.0, Build 17134)
• System Manufacturer: Alienware*
• System Model: Alienware Area-51* R4
• SSD: NVMe KXG50ZNV1T02 NVM
• Memory: 32 GB DDR4, ~1.3 GHz

Resources

Fog, Agner, PhD: Software Optimization Resources

Intel^® SPMD Program Compiler

Intel^® Intrinsics Guide

Lomont, Chris: Introduction to Intel® Intrinsics Guide

Sharma, Kamal; Karlin, Ian; Keasler, Jeff; McGraw, James R.; Sarkar, Vivek: Data Layout Optimization for Portable Performance

uncredited: Programming Guidelines for Vectorization