Performance Benchmarks: Intel® oneAPI Math Kernel Library on the Latest Intel® Xeon® Processors

Introduction

The 4^th Gen Intel® Xeon® Scalable Processor launched with many new capabilities and architectural advances, including having the most built-in accelerators of any CPU on the market¹. It behooves developers to ensure their software takes full advantage of these latest improvements. A chief way to achieve this is by using the latest performance libraries, optimized to unleash the new Intel Xeon Processor’s latest instruction set and architecture advances.

To this end, we are providing updated benchmark data of the Intel oneAPI Math Kernel Library (oneMKL), measured on the new processor. These benchmarks are offered to help you make informed decisions about which routines to use in your applications. They cover performance for each major function domain in oneMKL by processor family. Some benchmark charts only include absolute performance measurements for specific problem sizes. Others compare previous versions as well as popular alternate open-source libraries and other standard-function implementations with oneMKL.

We provide guidance on performance scaling across available thread utilization and data types. oneMKL for instance directly leverages Intel® Advanced Matrix Extensions (Intel® AMX) to optimize matrix multiply computations for BF16 and INT8 data types. This can directly benefit many convolutional filtering and linear algebra use cases.

Here, we touch upon all key functional domains: Linear Algebra (BLAS, LAPACK), Vector Math, Fast Fourier Transforms (FFT), Random Number Generation (RNG) as well as Direct Sparse Solvers (PARDISO).

Linear Algebra (BLAS and LAPACK)

Let us start with insights into performance characterization for linear algebra.

One reference is standard single-precision General Matrix Multiplication (GEMM) performance compared with performance using the newly supported BF16 data type on oneMKL. GEMM is commonly used for machine learning using matrix multiplication in neural networks, scientific computing such as numerical simulations, and several other inference and training operations. (Figure 1)

General Matrix Multiplication (GEMM)

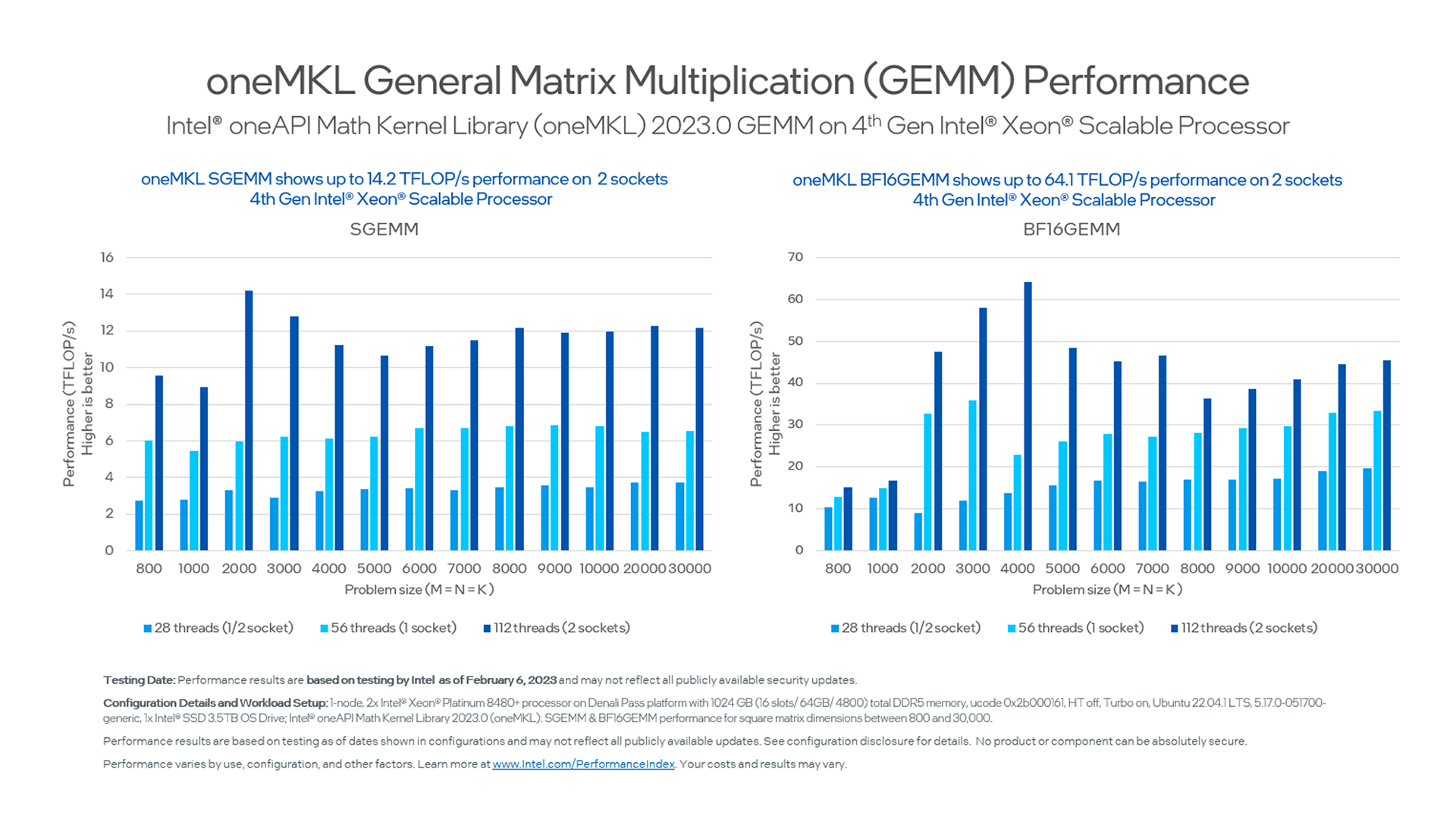
Figure 1. oneMKL GEMM Performance with BF16 Data Type

As we can see, depending on the problem size and number of threads available on the 4^th Gen Intel Xeon Scalable Processor, oneMKL allows you to execute BF16 matrix multiply operations up to 4 times faster than regular single-precision matrix multiply.

Takeaway: Machine learning workloads and other workloads that take advantage of this data type can be accelerated significantly. This is something worth considering while you design your application or define an execution path for the latest generation of Intel server processors.

Reference oneMKL Code Sample for GEMM on GitHub:

• Block LU Decomposition shows how to use the Intel® oneAPI Math Kernel Library (oneMKL) BLAS and LAPACK functionality to solve a block tridiagonal linear equation.

Linear Algebra Package (LAPACK)

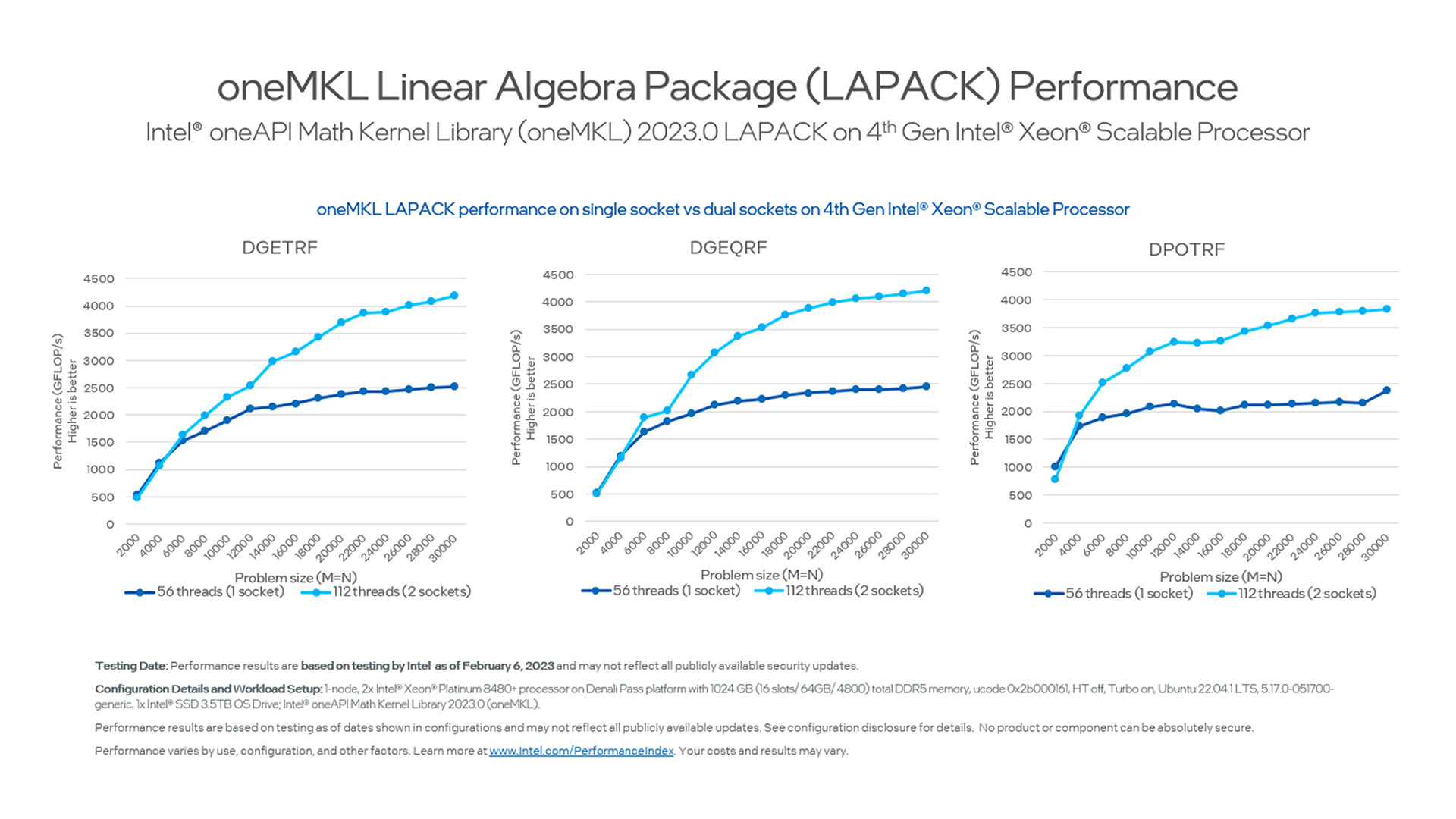
Figure 2. LAPACK Performance Scaling with varying Problem Size

As we look at numerical linear algebra functions and look at the scaling of factorization performance with increasing problem size, the degree to which these operations benefit from threading becomes obvious. The peak performance level for a dual-socket system scales directly with the number of available threads and, as such, almost double that of a single-socket system. In addition, the maximum performance saturation point is reached later at larger problem sizes.

Takeaway: As your intuition may have already told you, having more threads available for your linear algebra computation becomes more important with bigger problem sizes.

Reference oneMKL Code Samples for LAPACK:

• Linear Equations
• Linear Least Square Problems
• Symmetric Eigenproblems
• Nonsymmetric Eigenproblems
• Singular Value Decomposition

Learn More about LAPACK:

• LAPACK Function Finding Advisor for Intel® oneAPI Math Kernel Library (oneMKL)

Sparse Matrix-Vector (SpMV)

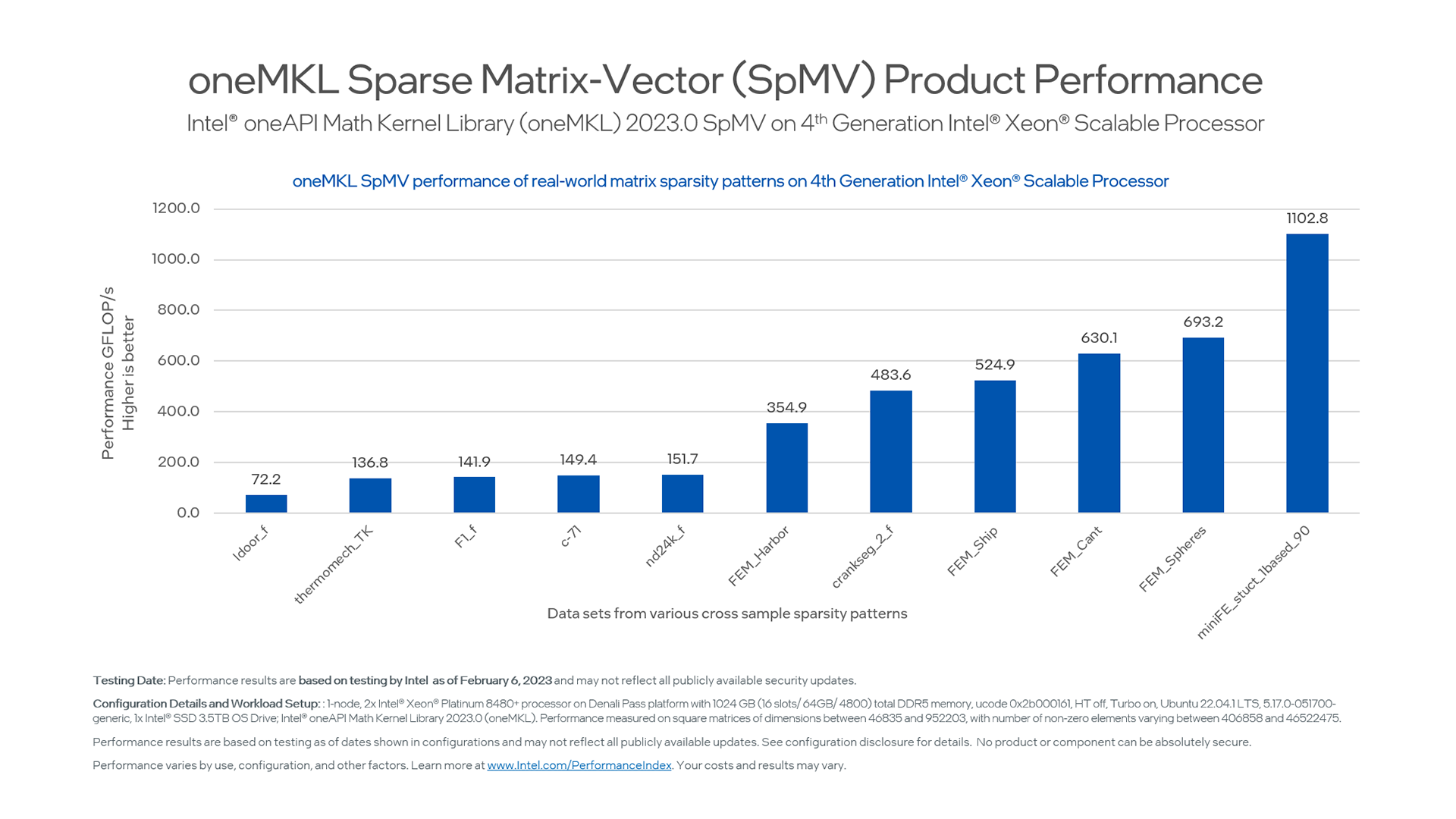
Figure 3. Sparse Matrix-Vector Performance

Figure 3 highlights the Sparse Matrix-Vector (SPMV) math performance for different routines on the latest Intel Xeon Scalable Processor generation.

Takeaway: Using the latest generation of oneMKL together with the latest generation of hardware allows you to benefit directly from hardware and software advances without modifying your code basis.

Reference oneMKL Syntax Sample for SPMV on GitHub.

Learn more about Sparse Matrix-Vector Functions:

• Sparse Matrix-Vector Functions Developer Reference

Vector Math (VM)

Figure 4. Vector Math Performance Impact of High Precision

As you probably expect, there is a performance impact of choosing high-precision, high-accuracy operations in vector math. For single-precision, the increase in clock cycles needed per vector element for higher result accuracy is on the order of 25% and thus acceptable in many cases.

However, when using vector math on double-precision data, verifying what level of accuracy you require for your results becomes way more important. There are two general rules here:

1. Always use the minimum level of accuracy required for your use case.
2. If your workload performance is not what you desire, use a performance-analysis tool like Intel® VTune Profiler to check for hotspots in code regions using high-precision data.

Takeaway: If the analysis tool pinpoints hotspots in a code region, you will want to consider whether you really need high-accuracy results for that operation. Additionally, if your workload uses task parallelism, this may indicate an opportunity to rebalance your parallel workload distribution. Locks and Waits analysis as well as CPU core utilization should help you identify those opportunities.

Reference VM Code Samples:

• Unzip the examples_core_c.tgz archive file in the examples folder of the Intel® oneAPI Math Kernel Library installation directory. The default location for the example archive files on a Linux system is /opt/intel/oneapi/mkl/latest/examples/. Reference oneMKL Code Samples for Vector Math function usage can then be found at ${MKL}/examples/c/vml/source.

Learn more about Vector Math:

• Vector Math Functions Developer Reference

Fast Fourier Transform (FFT)

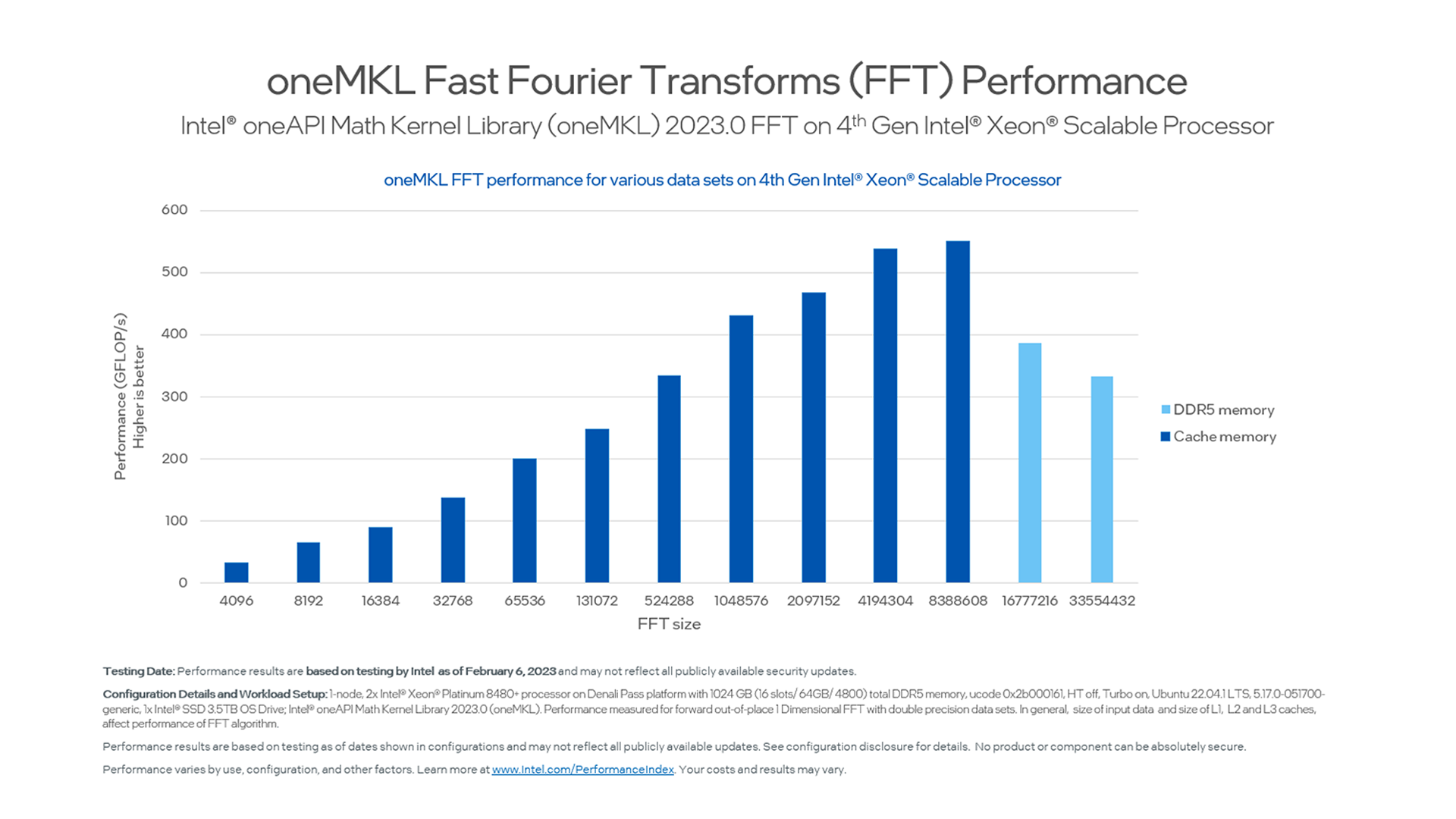
Figure 5. Fast Fourier Transform Performance with Increasing FFT Size

The performance curve of FFTs highlights the benefit of having large, directly addressable memory available on a server platform for memory-bound workloads. In addition, it demonstrates how having support for the latest low-latency DDR5 memory technology with Intel Xeon Scalable Processors helps to drive better performance for FFTs and other memory-bound operations.

Takeaway: From a software architecture and code-design perspective, you get the best performance by tailoring the FFT size to the available platform memory. The performance increases significantly until you reach the memory saturation point for your workload. Once you cross that point, there will be a penalty for cache usage. For the best performance of these kinds of workloads, best possible memory utilization is the key.

Reference oneMKL Code Sample for FFT on GitHub:

• Implement the Fourier correlation algorithm using SYCL, oneMKL, and oneDPL functions.

Learn more about FFT Functions:

• Efficiently Implementing Fourier Correlation Using oneAPI Math Kernel Library (oneMKL)
• Accelerating the 2D Fourier Correlation Algorithm with ArrayFire and oneAPI

Parallel Direct Solver (PARDISO)

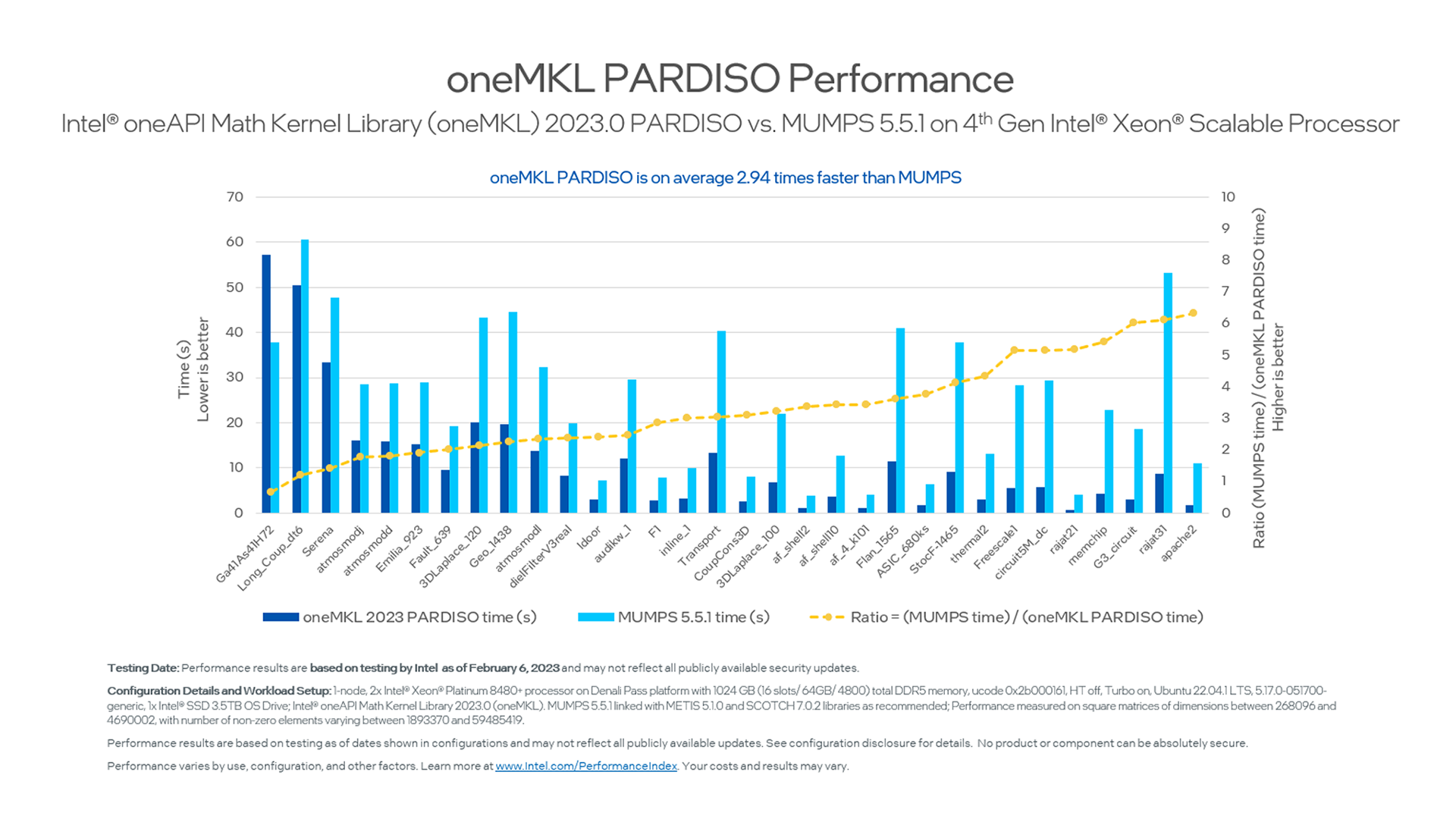
Figure 6. oneMKL 2023.0 Performance compared with MUMPS* 5.5.1

Across the spectrum, oneMKL’s Parallel Direct Sparse Solver (PARDISO) interface consistently outperforms and computes significantly faster than MUMPS 5.5.1 (Multifrontal Massively Parallel sparse direct Solver) on our latest server processor-based platforms. The oneAPI Math Kernel Library PARDISO solver helps with analysis and symbolic factorization, numerical factorization, and forward and backward substitution including iterative refinement and termination to release all internal solver memory.

Takeaway: If your workload’s performance relies heavily on sparse solvers, we recommend you have a closer look at oneMKL PARDISO.

Reference oneMKL Code Samples for PARDISO:

• Unzip the examples_core_c.tgz archive file in the examples folder of the Intel® oneAPI Math Kernel Library installation directory. Reference oneMKL Code Samples for PARDISO function usage can then be found at ${MKL}/examples/c/pdepoisson/source.

Learn more about oneMKL PARDISO:

• oneMKL PARDISO - Parallel Direct Sparse Solver Interface

Random Number Generator (RNG)

Figure 7. oneMKL Random Number Generator Performance compared to Standard C rand()

If you do not just use a random number at the very beginning of your workload as a computational seed, but instead your workload relies heavily on RNG, relying on standard library function calls will simply not do the trick.

For instance, Monte-Carlo simulation is used in risk management across a multitude of applications such as finance, computational physics, engineering, high-end gaming for path tracing or Monte-Carlo tree search, and modeling of complex systems. In all these cases, a highly optimized random number generation library is a must.

RNG performance also scales directly with the ability for parallel execution and thus the availability of threads.

Takeaway: On a 4^th Gen Intel Xeon Scalable Processor based platform, not only is RNG 45 times faster in single-threaded execution versus the stock STL function, but execution speed also increases another 18-fold if you take advantage of all the available 112 hardware threads/dual socket.

Reference oneMKL Code Samples for RNG on GitHub:

• Monte Carlo European Options: See how to use the oneMKL random number generator (RNG) functionality to compute European option prices.
• Black-Scholes: Learn how to use vector math and the RNG available in oneMKL to calculate the prices of options using the Black-Scholes formula.

Learn more about oneMKL RNG:

• oneMKL RNG Device Usage Model

Summary

The Intel oneAPI Math Kernel Library 2023.0 comes with the latest optimizations for the 4^th Gen Intel Xeon Scalable Processor.

Additionally, it fully enables major performance gains stemming from the architectural advances in the 4^th Gen Intel Xeon Scalable Processor. Whether is Intel® Advanced Matrix Extensions (Intel® AMX), Intel® Advanced vector Extensions 512 (Intel® AVX-512) or BF16 data types, oneMKL is the ticket to leverage Intel’s latest technology for computational math.

Additional Resources

Be sure to check out details about software support for the latest Intel Xeon Scalable Processor including the Intel® oneAPI based software development use cases. Here are more resources you may be interested in:

• Intel® oneAPI Math Kernel Library Getting Started Guide
• Intel® oneAPI Math Kernel Library (oneMKL) - Data Parallel C++ Developer Reference
• Intel® oneAPI Math Kernel Library Link Line Advisor
• Developer Reference for Intel® oneAPI Math Kernel Library for Fortran
• Developer Reference for Intel® oneAPI Math Kernel Library for C
• Software for 4^th Gen Intel® Xeon® and Intel® Max Series Processors

Get the Software

Download the Intel® oneAPI Math Kernel Library (oneMKL) stand-alone or as part of the Intel® oneAPI Base Toolkit, a core set of tools and libraries for developing high-performance, data-centric applications across diverse architectures.

Configuration and Setup Details

• Hardware Configuration:
  • 1-node, 2x Intel® Xeon® Platinum 8480+ processor on Intel® Server System D50TNP Family platform
  • 1024 GB (16 slots/ 64GB/ 4800) total DDR5 memory,
  • ucode 0x2b000161, HT off, Turbo on
  • 1x Intel® SSD 3.5TB OS Drive
• Operating System: Ubuntu 22.04.1 LTS, 5.17.0-051700-generic
• Intel® oneAPI Math Kernel Library 2023.0 (oneMKL)

Performance results are based on testing as of dates shown in configurations and may not reflect all publicly available updates. See configuration disclosure for details.  No product or component can be absolutely secure.

Performance varies by use, configuration, and other factors. Learn more at www.Intel.com/PerformanceIndex. Your costs and results may vary.