Intel is pleased to announce the release of the Intel® Homomorphic Encryption Acceleration Library (Intel® HE Acceleration Library) for FPGA, an open-source code library, under the Apache 2.0 license, as our contribution to the developer community.
The Intel® HE Acceleration Library has been designed with developers in mind and is intended to bridge the gap between register-transfer level (RTL) designers and cryptography experts. This release comprises baseline implementation of FPGA processing elements (FPGA kernels), source code that allows developers to experiment with and evaluate the functionality of number-theoretic transform, and dyadic multiplication functions.
Kernel developers will find OpenCL kernel examples with a host code in C++ to evaluate homomorphic encryption primitives. The Intel HE Acceleration FPGA library also provides example benchmarks, documentation, a list of reference articles, and links to tools and resources.
Library developers will find an example of how to integrate kernels with their libraries, and an example on how the host dispatches library requests to the FPGA.
Application developers will find an example of API and kernels integration with application code.
The FPGA library implements the following primitives:
- The forward negacyclic number-theoretic transform (NTT).
- The inverse negacyclic number-theoretic transform (INTT).
- Dyadic multiplication.
Each primitive is implemented in Intel® OpenCL 2.0. This distribution contains an experimental integrated kernel implementing the NTT/INTT and the dyadic multiplication in one file, as well as separate standalone kernels each implementing one of the primitive functions. All the FPGA kernels work independently of each other. The standalone kernels allow testing and experimentation of a single primitive. Note that this distribution in its current version does not fully address the inherent I/O bottlenecks typically associated with an external accelerator card; thus, it allows experimentation with basic building blocks and the study of bottlenecks mitigation.
Overview
Homomorphic Encryption (HE) belongs to a class of advanced cryptographic techniques for privacy-preserving computation. HE enables computation on encrypted data without ever having to decrypt it. HE is considered the holy grail of cryptography because the data remains encrypted throughout its lifecycle, at rest, in transit and when it is computed on. Arbitrary computation on encrypted data has been an open problem since the late 1970's, until Craig Gentry in 20091 described the first construction of a Fully Homomorphic Encryption (FHE) scheme that made it possible to construct circuits to perform arbitrary computation on encrypted data.
FHE is built on the hardness of the mathematics of lattice problems2,3. Lattice-based cryptographic constructions that rely on the worst-case hardness of lattice problems offer strong provable post-quantum computing security guarantees4,5 and are instrumental in the creation of secure cryptosystems. Since 2009, many types of FHE mathematical schemes and FHE software libraries implementing these schemes have been proposed. Thanks to these libraries, application developers now have the APIs needed to build privacy-preserving solutions. HELib6, MS SEAL7, and PALISADE8 are among the most popular open source FHE software libraries. They differ in implementation, performance, and support different FHE schemes. However, they share common algorithms using modular polynomial arithmetic operations on large integers.
The complexity of modular polynomial arithmetic operations on large integers and the size of the encrypted data (ciphertexts) incur computational and I/O bottlenecks. Computing on encrypted data is orders of magnitude slower than computing on regular, non-encrypted data. Accelerating the computation and I/O involved in FHE is one of the key requirements for broad commercial adoption of HE technology. The open-source FPGA library has been designed so practitioners can address acceleration requirements, devise optimizations and simplifications at a low algorithmic level, and also implement system-level optimizations to integrate primitives in applications.
Intel® HE Acceleration Library provides baseline implementations of FPGA kernels to support the basic number-theoretic polynomial operations commonly used in homomorphic encryption arithmetic based on lattice-based cryptography2,4,11. Operations of lattice-based cryptosystems involve modular polynomial arithmetic, including element-wise polynomial additions, element-wise polynomial subtractions, elementwise polynomial multiplications, and polynomial-polynomial multiplications. These building blocks are intended to improve system-level throughput performance of privacy-preserving applications based on homomorphic encryption.
Modular Polynomial Arithmetic in a Nutshell
To understand the mathematics of modular polynomial arithmetic used in lattice cryptography implemented in the Intel HE Acceleration Library, let’s review linear algebra products and explain their implementations in FPGA kernels.
In lattice cryptography, the common building blocks typically operate on the domain of polynomial quotient rings \(R = Z/qZ[X]/(X^N + 1)\). Those polynomials of at most N-1 degree have their coefficients as integers in the finite field \(Z/qZ = {0, 1, ..., q - 1},\) where q denotes a multi-precision prime number, N is conventionally a power of 2, and the q ≡ 1 mod 2N equation is satisfied. The parameters N and q form the basis of the security level strength. Finally, the encrypted data consists of a pair of polynomials \(c = (a, b) \in R \frac {2}{q}\) where c is referred to as a ciphertext. Therefore, the common algorithmic building blocks of lattice cryptography involve polynomial ring arithmetic, including modular polynomial additions and multiplications.
Polynomials are typically represented as a vector of coefficients \(a={a_0,a_1,…,a_(N-1) }\). First, let’s recall the definitions of Kronecker product ⊗ (tensor product) and Hadamard product ⊙ (element-wise product):
\(a= \begin {matrix} a_x \\ a_y \\ a_z \end {matrix}\) \(b= \begin {matrix} b_x \\ b_y \\ b_z \end {matrix}\)
\(a⊙b= \begin {matrix} a_x b_x \\ a_y b_y \\ a_z b_z\end {matrix}\)
\(a⊗b= \begin {matrix} a_x b_x & a_y b_y & a_z b_z \\ a_x b_x & a_y b_y & a_z b_z \\ a_x b_x & a_y b_y & a_z b_z \\ \end {matrix}\)
A ciphertext-ciphertext addition consists of element-wise vector additions and a ciphertext-ciphertext multiplication turns into a tensor product.
\(c⊗c'=(a,b)⊗(a',b' )→(a⊙a',a⊙b'+b⊙a',b⊙b' ) \in R_q^3\)
Each matrix coefficient is computed modulo q. The tensor product ⊗ creates three vectors from the two initials, resulting in a ciphertext in \(R_q^3\). An additional operation, named relinearization, will restore a ciphertext in \(R_q^2\) with only two vectors. The support for the relinearization operation will be included in a later release. A detailed explanation of these operations can be found here9.
The naive implementation of the tensor product ⊗ operation has O(N2) computational complexity. To perform ciphertext-ciphertext multiplication more efficiently in O(N log N) asymptotic complexity, we use the number-theoretic transform (NTT). NTT is a Fast Fourier Transform (FFT) over a finite field of integers, such that additions and multiplications are performed modulo q. NTT is a performance bottleneck for lattice-based encryption schemes and many algorithms and solutions have been proposed to speed up its performance10, 11, including with accelerators such as GPUs12 and FPGAs13,14. The NTT/INTT that we have implemented is an in-place radix 2 transform for real inputs which benefits from symmetries between real and imaginary parts.
Which Primitives are Implemented as FPGA Kernels
The list of operations used in homomorphic encryption that are provided in the Intel® Homomorphic Encryption Acceleration Library for FPGA open-source release include:
- Forward and Inverse NTT. Both the forward (NTT) and inverse (INTT) implementations of the number theoretic transform algorithm are included. NTT is equivalent to a Discrete Fourier Transform (DFT) over a finite field of integers12, 13. In our implementation, twiddle factors are kept constant and loaded just once. NTT API calls can be synchronous (blocking and slow), as well as asynchronous for a specific code block where calls are made to offload NTT (or INTT) work only. Asynchronous calls are possible provided that the same set of twiddle factors is reutilized in all the calls. The ciphertexts subject to NTT processing are internally buffered and batched for processing in the FPGA.
- Dyadic Multiplication. To multiply two ciphertexts, we assume that they have been transformed into their NTT form to perform an NTT-based polynomial multiplication.
- For example: the tensor product â ⊗ b̂, where â = NTT (cta) = (NTT (a0), NTT (a1)) and b̂ = NTT (ctb) = (NTT (b0), NTT (b1)). The dyadic multiplication API calls can be either synchronous or asynchronous. In the asynchronous case, the same rules as for NTT apply. As previously mentioned, the resulting ciphertext has three components and needs to be relinearized on the host side by the programmer.
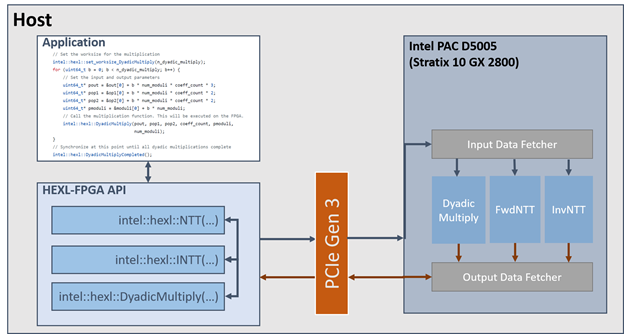
Figure 1 gives an overview of the content of this release and the software stack. The figure mentions HEXL-FPGA API which is the name given in the source code for Intel® Homomorphic Encryption Acceleration Library for FPGA API. A host application makes asynchronous Intel® Homomorphic Encryption Acceleration Library for FPGA API calls inside a code block defined by a for loop. Multiple asynchronous calls to the dyadic multiplication operation are issued. Input data for each dyadic multiplication resides in a contiguous memory space. In the inner body of the for loop, intel::hexl::DyadicMultiply(...) work requests are enqueued in a buffer and sent to the FPGA in smaller chunks of data called batches. At the end of the for loop code block, the program waits until all the work for the set of calls has been completed, where intel::hexl::DyadicMultiplyCompleted(...) works as an explicit barrier. On the device side, a batch of data is pulled and delivered for processing to the target kernel. The output data fetcher waits for the batch processing completion before sending the results back to host through the PCIe. Since this mechanism is asynchronous, data movement overlaps as much as possible with FPGA compute work.
How We Optimized the Code
As only basic HE primitives are provided in this release, only a limited number of optimizations are shown in this code. A greater deal of optimizations will be needed at the system level in a commercial application. This release provides the foundations and the flexibility for developers to implement such optimizations based on the requirements of their applications. To understand the low-level optimizations implemented in each kernel, refer to the Intel FPGA SDK for OpenCL Best Practice Guide. A careful examination of Intel® Homomorphic Encryption Acceleration Library for FPGA source code will show how these principles were applied to get the most of the kernel's performance on batched execution.
At the system level, the FPGA library API is driven by the accelerator demand for data. System level throughput is achieved through non-blocking API calls where preprocessing and post-processing asynchronously overlap I/O data transfer and kernel computation. To optimize the kernels, we analyzed the reports generated by the aocl compiler and HLS tool. Based on this analysis, we inferred which changes were required in the code. This is an iterative process where an issue is detected in the compiler report, a code adjustment is developed, and the change is validated before adoption.
The main optimization techniques involve loop fusion, double buffering, vectoring, and burst memory access. In addition, we introduce loop-unrolling (data parallelization) and functional concurrency with deep pipelining (loop pipelining). Better latency and data locality were achieved with data prefetching, memory coalescing, BRAM banking, bank conflicts resolution through data reordering and replication, data packing, and data reuse.
After having experimented with our open-source code and kernels, the practitioner will find that system-level optimization is critical to improve performance throughput, especially for I/O bound compute building blocks. Deciding when a variable like twiddle factors or normalization factors need to be read from memory or computed on the fly is also an important design choice.
Pipeline profiling is instrumental to improve FPGA computational performance while minimizing resource usage. For that matter we used extensively the aocl compiler reports, Intel tools such as the VTune™ analyzer and OpenCL Intercept Layer to measure host-FPGA interactions. The art of the FPGA designer is to leverage the strengths of the FPGA, namely architecture flexibility, the ability to stream data and to optimize pipeline execution while avoiding excessive complexity. Intel® OpenCL provides an effective solution for fast prototyping of the FPGA application design. It’s a tradeoff between performance and development time.
The library kernels were validated on a system hosting an Intel® PAC D5005 (Stratix 10 GX 2800, such as in reference 12) PCIe card. Additionally, host side support is provided through a C/C++ FPGA Runtime API that can be used to launch the kernels and execute them in the FPGA.
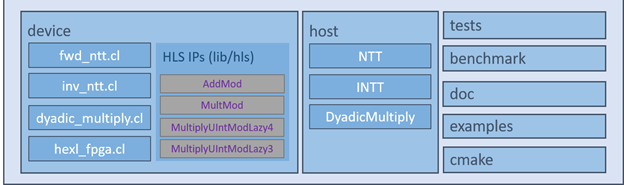
Figure 2 shows an overview of the components that make up the Intel® Homomorphic Encryption Acceleration Library for FPGA package.
Call to Action
This distribution is the beginning of a journey that Intel hopes to travel with the cryptographic community. We have many ideas for upcoming releases, and we encourage you to contribute with your own designs. In the future, we plan to port the library to Intel® oneAPI, a unified programming paradigm for heterogeneous computing. We will also add new functionalities to support more homomorphic encryption operations, such as relinearization and rotation. As a member of the community of HE practitioners, you are invited and welcomed to contribute to this effort with new optimizations, additional FPGA kernels, as well as by extending the C/C++ Intel® Homomorphic Encryption Acceleration Library for FPGA Runtime API.
References
- Craig Gentry. Fully homomorphic encryption using ideal lattices. In Proceedings of the forty-first annual ACM symposium on Theory of computing, pages 169–178, 2009.
- Dong Pyo Chi, Jeong Woon Choi, Jeong San Kim, and Taewan Kim. Lattice based cryptography for beginners. IACR Cryptol. ePrint Arch., 2015:938, 2015.
- Craig Gentry. Toward basing fully homomorphic encryption on worst-case hardness. In Annual Cryptology Conference, pages 116–137. Springer, 2010.
- Daniele Micciancio and Oded Regev. Lattice-based cryptography. In Post-quantum cryptography, pages 147–191. Springer, 2009.
- Hamid Nejatollahi, Nikil Dutt, Sandip Ray, Francesco Regazzoni, Indranil Banerjee, and Rosario Cammarota. Post-quantum lattice-based cryptography implementations: A survey. ACM Computing Surveys (CSUR), 51(6):1–41, 2019.
- Shai Halevi and Victor Shoup. Design and implementation of helib: a homomorphic encryption library. Cryptology ePrint Archive, Report 2020/1481, 2020. https://ia.cr/2020/1481.
- Microsoft* SEAL (release 3.7). https://github.com/Microsoft/SEAL, September 2021. Microsoft Research, Redmond, WA.
- PALISADE Lattice Cryptography Library (release 1.11.2). https://palisade-crypto.org/, May 2021.
- Daniel Huynh, Privacy-Preserving Data Science Explained series, CKKS explained part-4 multiplication and relinearization, (2020) https://blog.openmined.org/ckks-explained-part-4-multiplication-and-relinearization/
- Fabian Boemer, Sejun Kim, Gelila Seifu, Fillipe DM de Souza, Vinodh Gopal, et al. Intel HEXL (release 1.2). https://github.com/intel/hexl, 2021.
- David Harvey. Faster arithmetic for number-theoretic transforms. Journal of Symbolic Computation, 60:113–119, 2014.
- Sangpyo Kim, Wonkyung Jung, Jaiyoung Park, and Jung Ho Ahn. Accelerating number theoretic transformations for bootstrappable homomorphic encryption on GPUs. In 2020 IEEE International Symposium on Workload Characterization (IISWC), pages 264–275. IEEE, 2020.
- Donald Donglong Chen, Nele Mentens, Frederik Vercauteren, Sujoy Sinha Roy, Ray C. C. Cheung, Derek Pao, and Ingrid Verbauwhede. High-speed polynomial multiplication architecture for ring-lwe and she cryptosystems. IEEE Transactions on Circuits and Systems I: Regular Papers, 62(1):157–166, 2015.
- M Sadegh Riazi, Kim Laine, Blake Pelton, and Wei Dai. Heax: An architecture for computing on encrypted data. In Proceedings of the Twenty-Fifth International Conference on Architectural Support for Programming Languages and Operating Systems, pages 1295–
1309, 2020. - Rivest, R.L., Adleman, L. and Deaouzos, M.L. (1978) On Data Banks and Privacy Homomorphism. In: DeMillo, R.A.. Ed., Foundations of Secure Computation, Academic Press, New York, 169-179.