DPEcho: General Relativity with SYCL* for the 2020s and beyond

Numerical sciences are experiencing a renaissance thanks to heterogeneous computing, which opens for simulations a quantitatively and qualitatively larger class of problems, albeit at the cost of code complexity. The SYCL* programming language offers a standard approach to heterogeneity that is scalable, portable, and open. It unlocks the capabilities of accelerators via an intuitive C++ API for work-sharing and scheduling, and for directly mapping simulation domains to the execution space. The latter is especially convenient in numerical general relativity (GR), a compute- and memory-intensive field where the properties of space and time are strictly coupled with the equations of motion.

The ECHO code¹ for general relativistic magneto hydrodynamics (GR-MHD) already features a recent HPC-optimized version (ECHO-3DHPC²) that is written in Fortran with hybrid parallelism via MPI+OpenMP. However, a SYCL rewrite was preferred over further work on the legacy code. In this paper, we introduce DPEcho, the MPI+SYCL version of GR-MHD. It is used to model instabilities, turbulence, propagation of waves, stellar winds and magnetospheres, and astrophysical processes around Black Holes. It supports classic and relativistic MHD, both in Minkowski or any coded GR metric. Our goals are to introduce the public version of DPEcho, to illustrate how SYCL is used to express the algorithm of a complex real-life application, and to quantify the performance achieved through this approach.

 CMAKE_BUILD_TYPE        Release
 SYCL                    oneAPI
 GPU                     ON  
 ENABLE_MPI              OFF
 SINGLE_PRECISION        OFF
 FILE_IO                 VISIT_BOV
 PHYSICS                 GRMHD
 METRIC                  CARTESIAN 
 FD                      4
 NRK                     2
 REC_ORDER               5
  
SYCL: Select the SYCL target architecture        
Keys: [enter] Edit an entry [d] Delete an entry   
      [l] Show log output   [c] Configure
      [h] Help              [q] Quit without generating
      [t] Toggle advanced mode (currently off)

Figure 1. Interactive ccmake terminal user interface of DPEcho

Getting Started with DPEcho

The public version of DPEcho is available on GitHub under an Apache II license. The code supports CMake and was designed with the interactive terminal user interface of ccmake in mind (Figure 1). DPEcho supports several SYCL compilers through this interface. The ccmake screen shows the code’s content: GPU support via SYCL queue selectors and MPI, single-precision, and I/O toggles. Next come the physics and numerical options: the solver can be switched between classical MHD and GR-MHD, one can cycle through the supported GR metrics according to the problem of interest (only Cartesian or Minkowski in the public version). The numerical options include different orders for numerical derivation (FD), variable grid reconstruction (REC), and Runge-Kutta solver steps (NRK: 1-3), similar to the original ECHO code.

The Intel® oneAPI Base Toolkit, a free implementation of the oneAPI specification, and the Intel® oneAPI HPC Toolkit were used to build, analyze, and run DPEcho on Intel CPUs and GPUs. The user can specify the mapping of MPI ranks to GPU resources (e.g., tiles) akin to the pinning of MPI ranks to CPU cores³. This is done at run time through environment variables. Performance analysis was done using the Intel VTune Profiler. Finally, the Intel® MPI Library can operate directly on memory segments located in the unified shared memory (USM), for example.

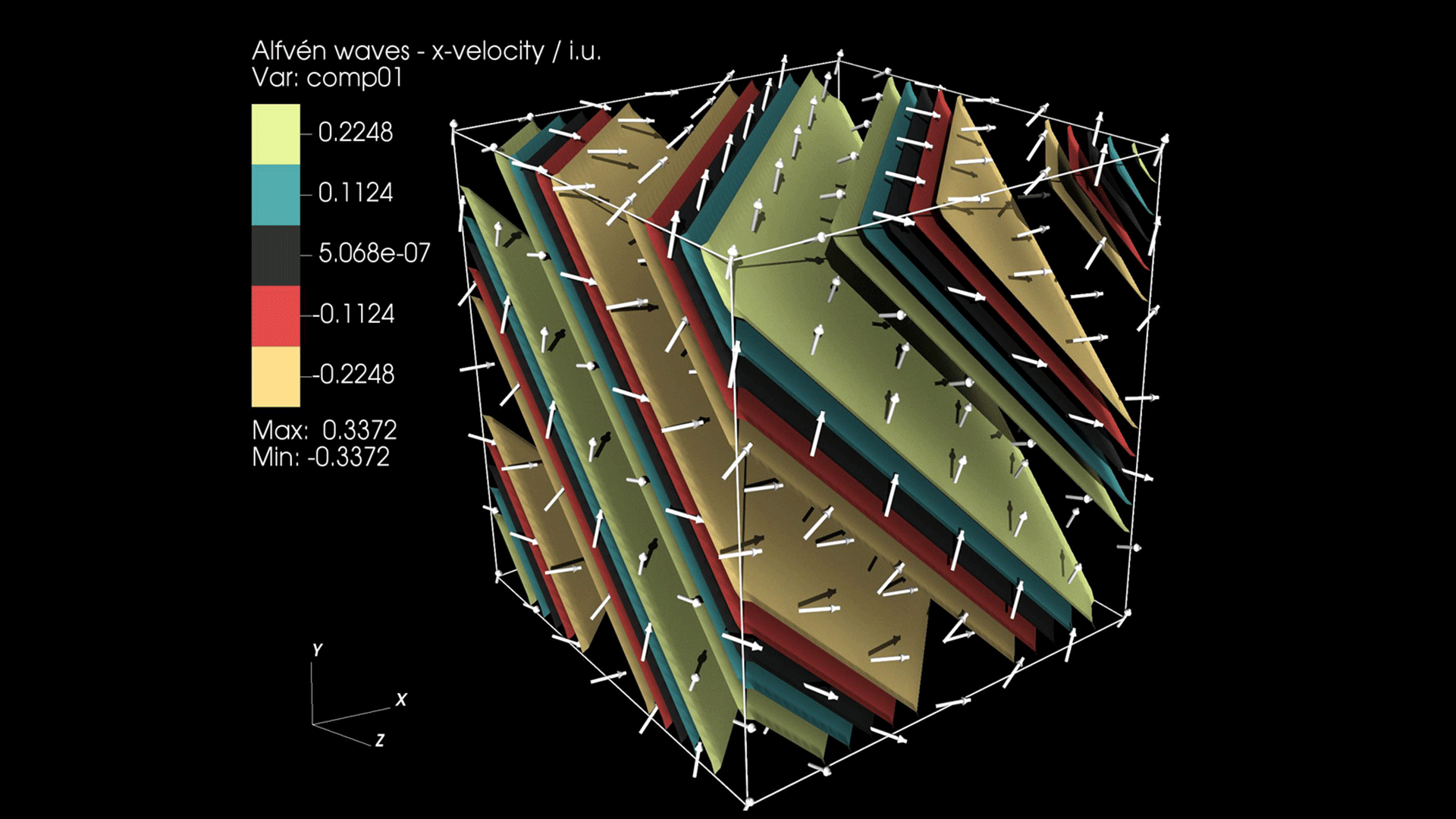
Figure 2. Rendering of planar Alfvén wave propagation in GR (x-velocity component) modeled with the public version of DPEcho. The arrows trace the magnetic field (uniform in magnitude)

The physics and numerical methods present in the public version of DPEcho allow for modeling of relativistic magnetized waves, such as the planar Alfvén waves, illustrated in Figure 2. Interfaces for modeling different problems (e.g., GR-MHD blast-waves) are present, but require user-defined implementations. A development version of DPEcho will include different GR metrics aimed at modeling the surroundings of rotating astrophysical black holes, as well as the general infrastructure for handling non-flat space-times. These features will not be released publicly. The authors will instead evaluate individual collaboration requests. Otherwise, the two versions have similar and compatible interfaces.

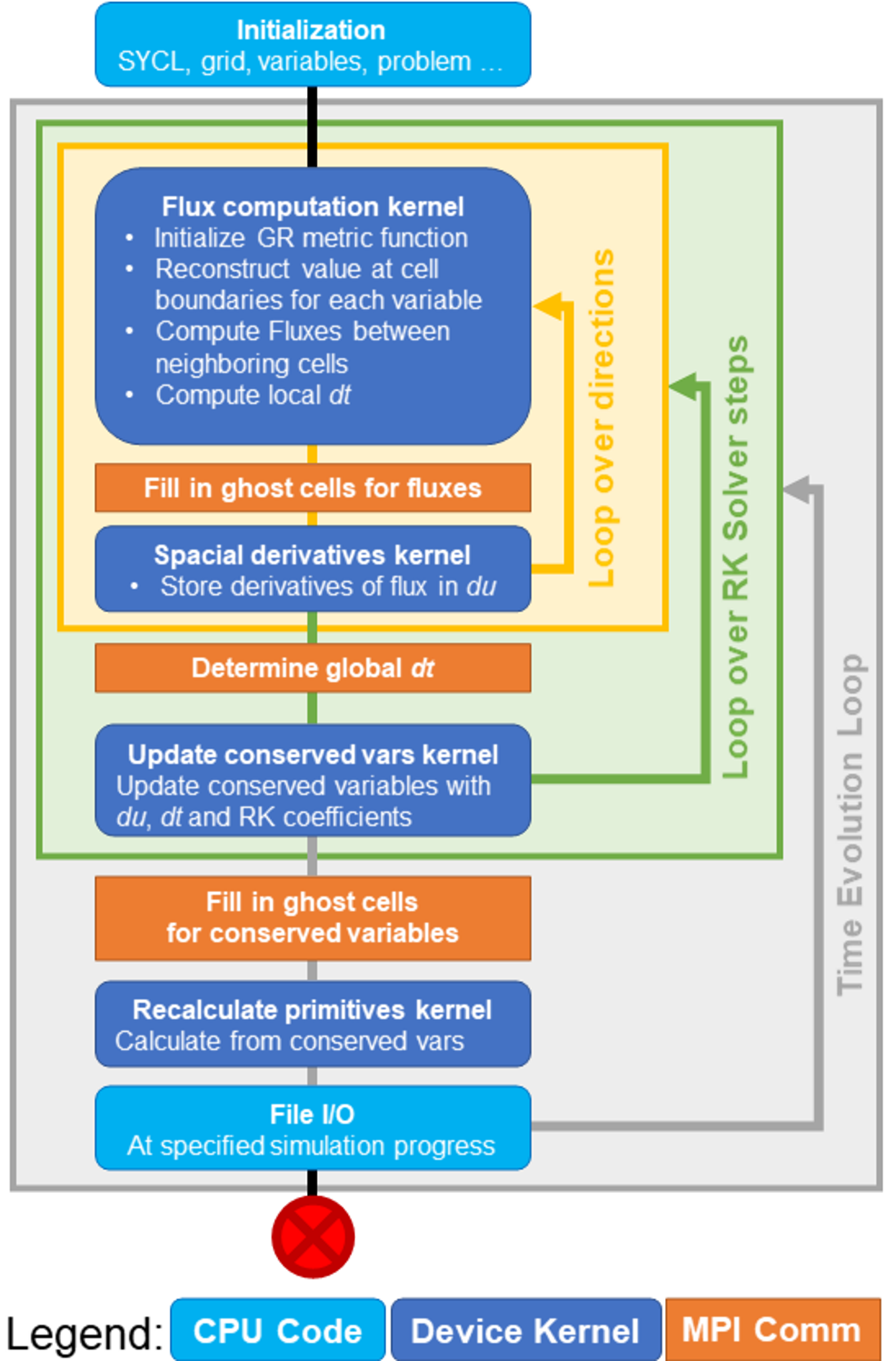
Figure 3. Logical overview of DPEcho

Main Structure of DPEcho

The main complication during DPEcho development was the redesign of the physical and numerical algorithms to support SYCL device-centric constructs. Figure 3 shows the host and device code, communication, and flow control of DPEcho. With careful planning and the adoption of USM, we were able to keep the main variable in the device memory for the entire run time. Data transfer is thus significantly reduced because the ghost layers around each MPI task’s domain (following a decomposition in an MPI cartesian grid) are copied through buffers of minimal size. Output dumping follows similar principles, in order not to lock the data on the device for further processing. Even using only simple SYCL control constructs (e.g., leaving out workgroups, shared local memory, queue dependencies), we can bypass data-transfer locks and achieve high performance with easily readable source code. Should more control be needed in future, these advanced features will be incorporated onto an already efficient basis without major foreseeable complications. This exemplifies the major advantages of SYCL.

Our USM usage is illustrated in Figure 4. First, we select the target device to offload computation, in this case the default GPU selected by the SYCL runtime. We allocate data directly in the device memory as a structure-of-arrays for the vector of unknowns. Allocating each vector component in its own array ensures that the runtime is able to partition the data correctly on tiled GPU architectures.

// Initialize the SYCL device and queue
sycl::gpu_selector sDev;  sycl::queue qDev(sDev);

// Allocate main variables with USM
double *v[VAR_NUM], *f[VAR_NUM], [...];
for (int i=0; i < VAR_NUM; ++i) {
  // Primitives and fluxes for each variable
  v[i] = malloc_device<double>(grid.numCells, qDev);
  f[i] = malloc_device<double>(grid.numCells, qDev);
  [...]
}

Figure 4. Allocation of the main variables in DPEcho by SYCL USM for direct device access

The bulk of the application’s computations are performed in the flux computation kernel (Figure 5). Aside from the fluxes, later steps of the iteration also require the computation of the maximum wave propagation speed, in order to determine a safe timestep increment. SYCL supports this through reduction kernels. For this, the parallel_for receives the shape of the computation plus a shared reduction object. In the device execution context, each work item then submits its local wave speed. Finally, the SYCL runtime determines the global maximum.

//-- SYCL ranges: grid size and local workgroup size
range<3> r = range(grid.nx, grid.ny, grid.nz),  rLoc = range(8, 8, 8);
 
[..] //-- Main code loops
  auto maxReduction = sycl::reduction(aMax+directionIndex, sycl::maximum<field>());
  qDev.parallel_for(nd_range<3>(r, rLoc), maxReduction, [=](nd_item<3> it, auto &amp;max) { 
  
   id<3> id    = it.get_global_id();              // SYCL indexes and offsets
   int myId    = globLinId(id, grid.nh, dOffset); // Custom index for ghost layer
   int dStride = stride(id, myDir, grid.nh);      
            
   // Declaring local variables on GPU registers
   double vRecR[VAR_NUM], vRecL[VAR_NUM] , ...; 
   Metric g(xCenter, yCenter, zCenter);    // Heart of GR: metric at each grid point
 
   // Space-aware function to interpolate each variable. -> THINK PARALLEL!
   holibRec(myId, v, dStride, vRecL,  vRecR);
   physicalFlux(directionIndex, g, vRecL, vRecR, ...); 
  
   [ ... ] // Compute characteristics from fluxes
   max.combine(localMax); // for time-stepping

Figure 5. Device code sample in DPEcho: parallel_for construct for flux calculation (partially abridged for clarity)

In the kernel, each work item computes the fluxes for a single grid cell. We use Grid, a custom “calculator class,” to map the work item global ID to grid cells, offsetting for the ghost layer. The first step is the creation of the Metric object, whose components are defined locally in each cell and are computed analytically, which helps avoid storing multiple additional variables. Next, for the computation of the fluxes, the kernel first needs to interpolate the values of the unknowns at the cell boundaries. We support different orders of reconstruction, to be configured at compile-time. This interpolation is performed in holibRec. The function uses the work item ID to determine its position in the simulation grid. Although it is not currently implemented, this function offers opportunities for work-sharing between neighboring work items. For example, the values at the center of the cell might be broadcast between cells to avoid redundant loads from global memory. After the interpolation, the computation of the fluxes is purely local, and hence embarrassingly parallel.

Performance Comparison

We present a scaling comparison of DPEcho versus the baseline ECHO, running the same problem setup (Figure 6). We first conduct a weak scaling test on the Intel Xeon 8174 nodes of SuperMUC-NG at the Leibniz-Rechenzentrum (Figure 6, left). We observe essentially flawless scaling up to 16 nodes, and performance (measured in millions of cell updates per timestep per wall clock second) up to 4x higher than the hybrid MPI+OpenMP baseline version. The reduced memory footprint of DPEcho allowed the placement of 384³ cells per MPI task, instead of 192³.

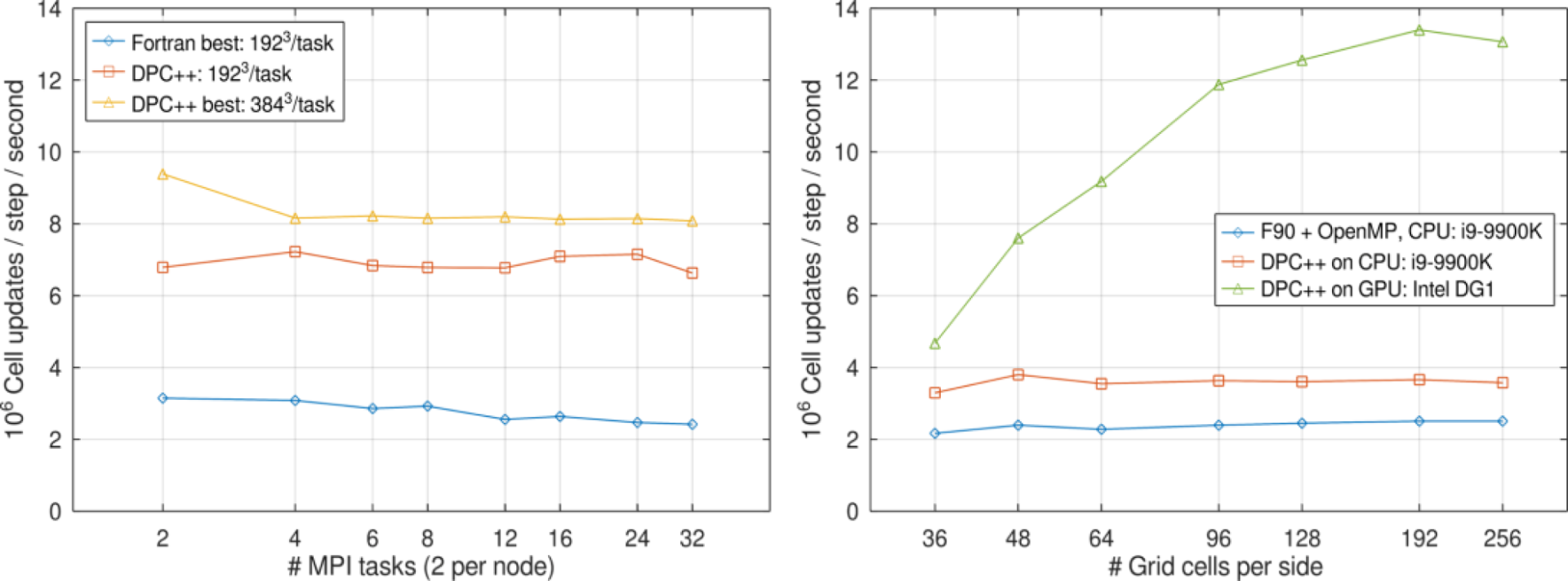
Figure 6. Performance comparison of ECHO (Fortran version) and DPEcho. Left: double-precision, CPU-only weak scaling test on HPC hardware (SKX node of SuperMUC-NG at LRZ). Besides a speedup of order 4, the decreased memory consumption allows for simulation boxes up to 8x larger. Right: single-precision test runs, increasing the grid size on consumer hardware (9th Generation Intel® Core™ i9 Processors with Intel® Iris® Xe MAX Graphics). The discrete graphics need large enough workloads, but rewards with performance comparable to non-accelerated HPC hardware.

Besides the HPC hardware, we also test consumer-grade hardware (Intel® Core™ i9-9900K Processor CPU with Intel® Iris® Xe MAX Graphics). This time we perform a grid-size scaling (Figure 6, right), always using the full node or device (switching to single-precision because of hardware limitations). The baseline performance on the CPU is in line with the HPC results. The inclusion of the Intel® Iris® Xe MAX Graphics increases performance up to 7x, surpassing even non-accelerated HPC hardware. This is a testament to the superior portability and efficiency of SYCL code, making the most efficient use of all classes of hardware.

Outlook and Discussion

DPEcho does not yet include a method to maintain the solenoidal condition of the magnetic field. In the original ECHO code, a strategy based on staggering of field components and multi-dimensional approximate Riemann solver for magnetic fluxes is adopted¹. However, this is rather involved, and we prefer to provide the community with a simple, extensible code where SYCL plays a fundamental role. The same is true for more complex physics, like the inclusion of non-ideal effects (e.g., physical viscosity, resistivity, dynamo terms in the induction equation). The development version will soon include curved spacetimes, with a test for the simulation of accretion from a disk onto a black hole in Kerr metric.

The potential of DPEcho, once all minimal upgrades are implemented, will certainly be high. 3D high-resolution simulations of the accretion inflow and the collimated jet launching from both supermassive and stellar-sized black hole systems could be studied in detail, with the potential to resolve in such global simulations both the ideal magneto-rotational instability and non-ideal plasmoid instabilities in tiny reconnection sites, minimizing the effects of numerical diffusion, which is always present in shock-capturing codes. For the time being, users are welcome to experiment with what is included the public version. Anyone interested in development collaborations is encouraged to contact the authors.

Get the Software