C++ API with SYCL* Support for Data Fitting

Story At-a-Glance

• oneMKL is a library of optimized math routines for science, engineering, and financial applications that has been around since May 2003. Its rich feature set made it the industry choice for core math functions since 2015.¹

• It covers BLAS, LAPACK, ScaLAPACK, sparse solvers, fast Fourier transforms, data fitting, random number generators, and vector math.

• In a first step, we enabled spline and cubic Hermite-based data fitting and interpolation to be directly accessible via a SYCL-compliant C++ API.

• It can be accessed directly by C++ code without the need for wrapper functions.

• Those computations can thus be seamlessly done on Intel® GPUs in addition to CPUs.

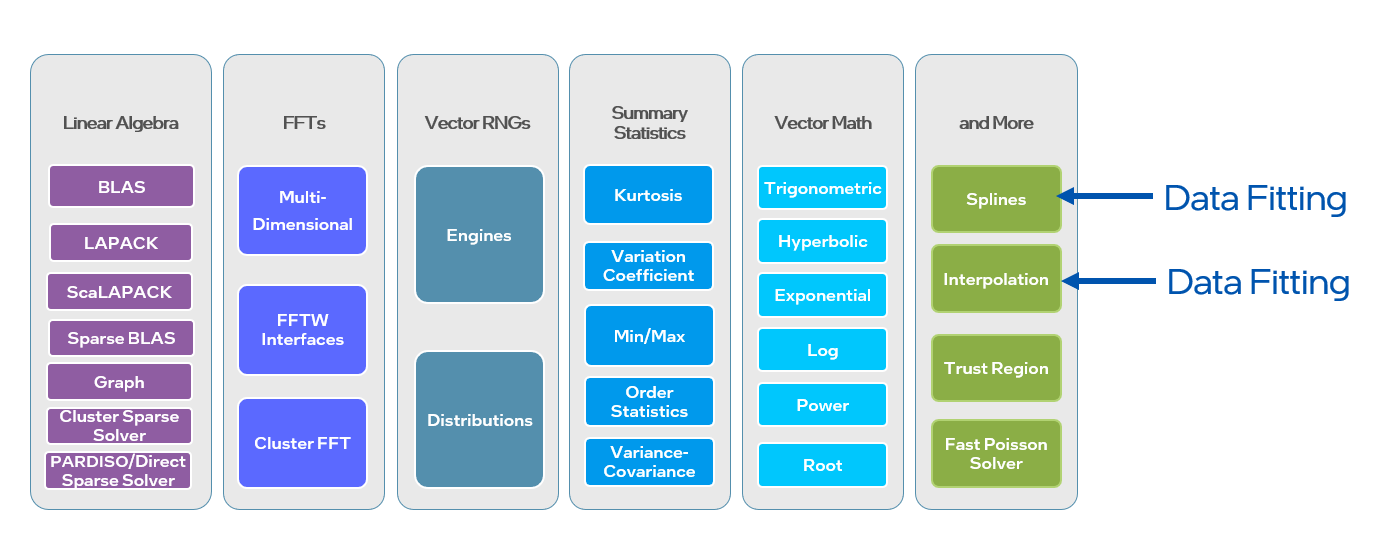
Figure 1. oneMKL Function Domains

Data Fitting with Interpolation Using Splines

Data fitting uses interpolation techniques constructing new data points based on the range of a discrete set of known data points.

Using spline curve functions defined piecewise as polynomials is frequently the preferred method. Applications cover a wide range of uses including science, healthcare, data science, neural networks, computer aided design, computer graphics, and gaming physics engines.

Traditionally the splining and interpolation routines used for this purpose are implemented using C or Fortran APIs, making it necessary to create a wrapper when integrating them into C++ code.

However, with the advent of heterogeneous parallel processing of data, C++ is becoming ever more popular as a language to implement data fitting.

One way to look at data fitting is as a set of functions to perform spline interpolation (function values and/or derivatives calculation) and integration.  Interpolation based on data fitting follows the following mathematical concepts:

Assume we need to interpolate a function \(f(x)\) on the \([a, b]\) interval using splines.

• Let us break \([a, b]\) into sub-intervals by n points \(x_i\) called partition points or simply partition.
• Function values at these points \((y_i=f(x_i ),ix_i),…,n\) are also given.
• Then we can call interpolation of \(f(x)\) at points of \([a, b]\). Such points are called interpolation sites or simply sites. Sites might or might not equal to partition points.
• After calling, users will have interpolation results.

Processing of multiple functions for one partition is also possible. Function values are stored in a one-dimensional array with \(nx * ny\) elements. Two different layouts are possible: row major and column major.

This one-dimensional array approach in both layouts is what is supported with our early implementation.

Nonetheless, it may also be desirable if each function for all partitions is stored in a separate memory location. That way, it can be implemented on request.

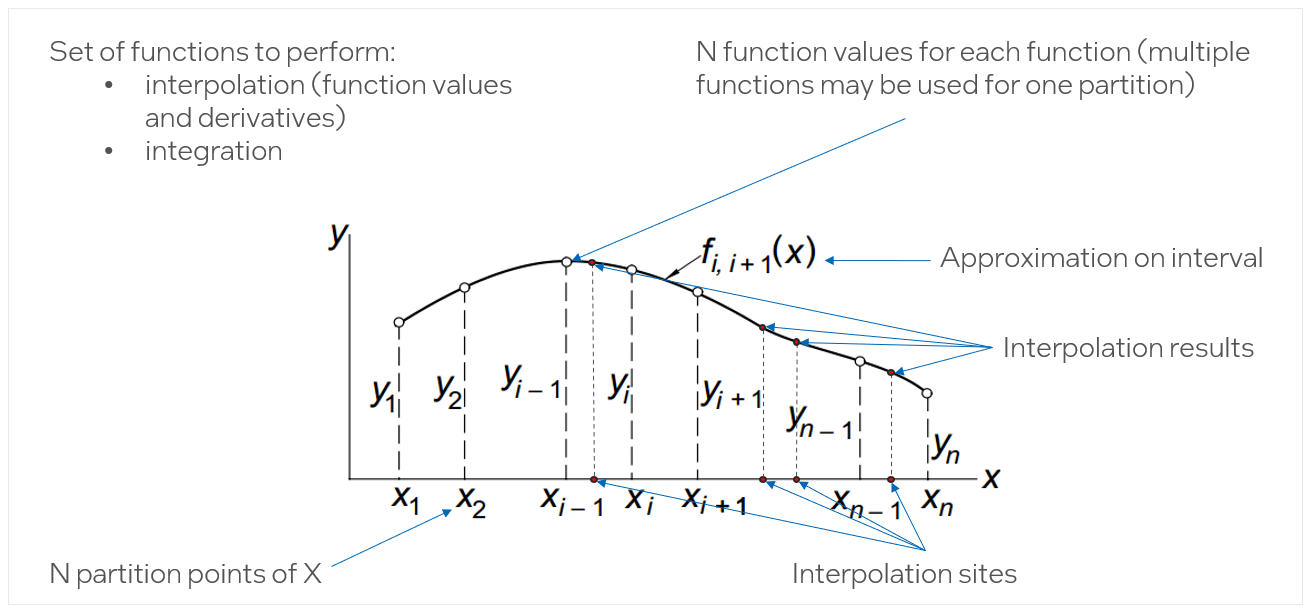
Figure 2. Interpolation using Spline Functions

With oneMKL 2022.1, a pre-release of SYCL (based on C++) support for interpolation using linear and cubic Hermite splines has been made available. This includes the construction of splines (produce spline coefficients) and interpolation, including function values and derivatives computation. We also provide handlers to store your input data.

The intent of all this work is to establish future-proof, standard C++ API support using SYCL. Once fully implemented, we will add it to our proposed API as part of the oneMKL specificiation. It will become part of the oneAPI industry-standards-based, unified, multiarchitecture, multi-vendor programming model.

Note: You can provide feedback and suggest changes or improvements to the interface now already on our community forum. We are looking forward to your input. This will ensure we best meet your software development requirements and integrate them in future releases.

Usage Overview

An overview of data fitting with oneMKL and detailed reference documentation are available as part of the oneMKL online documentation.  Let us, however, have a look at the SYCL-compliant C++ API usage of data fitting with oneMKL as a reference for how it may apply to your use case.

The standard usage flow is as follows:

1. Initialize spline parameters (e.g. quantity of points on the X axis, quantity of functions to process, coefficient memory allocation, etc.).  
2. Create date set handlers. You may want to change partition layout. This can be done using partition handlers. Using handlers simplifies spline customization versus the use of raw format template parameters inside a spline constructor.
3. Compute spline coefficients by calling the “construct” method of spline. Doing this outside of the spline constructor itself allows processing return data outside of the constructor. Additionally it allows you to control the exact point in time when the computation is performed during the execution flow.
4. The computed coefficients are now ready to use for interpolation.

#include "oneapi/mkl/experimental/data_fitting.hpp"

namespace  mkl_df = oneapi::mkl::experimental::data_fitiing;

int main() {
    std::int64_t nx = 100000; // quantity of x points
    std::int64_t ny = 5; // quantity of functions
    sycl::usm_allocator<float, sycl::usm::alloc::shared> alloc(q);

    std::vector<float, decltype(alloc)> partitions(nx, alloc);
    std::vector<float, decltype(alloc)> coeffs(ny * (nx - 1) * 2, alloc);
    std::vector<float, decltype(alloc)> functions(ny * nx, alloc);
…
    // memory allocation for sites, results, partitions 
    // and initialization of partitions, functions

    // Data Fitting usage
    // create spline object to accumulate all data
    mkl_df::spline<float, mkl_df::linear_spline::default_type> spl(q, ny);

    // handle partitions, coefficients and function values
    spl.set_partitions(partitions.data(), nx);
    spl.set_coefficients(coeffs.data());
    spl.set_function_value(functions.data());

    // compute spline coefficients
    auto event = spl.construct(); 

    // interpolate data basing on computed spline coefficients (async call in general)
    mkl_df::interpolate(spl, sites.data(), nsites, results.data()).wait(); 
…
}

Figure 3.  Data Initialization, Spline Creation, and Interpolation Usage Flow

Full and actual examples can be found on GutHub as part of the oneMKL examples, as well as the oneMKL Data Parallel C++ Developer Reference.

Interfaces

Let’s consider interfaces.

Note: Current interfaces are experimental and can be changed in future based on feedback from users.

The spline interface is defined as follows. We have two different constructors: one that accepts SYCL queue and one that accepts device and context.

An additional parameter is named “were_coeffs_computed” in case we want to use already precomputed coefficients.

• Copy/move constructors and copy/move assignment operators are deleted since the spline class is just a wrapper over memory that is managed by the user.
• The “construct” function performs coefficient calculation running on SYCL devices using queue from the constructor. Alternatively, it creates a new one from device and context if the corresponding constructor was called.

template <typename FpType, typename SplineType, int Dimensions = 1>
class spline {
public:
    using value_type = FpType;
    using spline_type = SplineType;

    spline(const sycl::queue& q, std::int64_t ny = 1, bool were_coeffs_computed = false);
    spline(const sycl::device& dev, const sycl::context& ctx, std::int64_t ny = 1, bool were_coeffs_computed = false);
    ~spline();
    spline(const spline<FpType, SplineType, Dimensions>& other) = delete;
    spline(spline<FpType, SplineType, Dimensions>&& other) = delete;
    spline<FpType, SplineType, Dimensions>& operator=(const spline<FpType, SplineType, Dimensions>& other) = delete;
    spline<FpType, SplineType, Dimensions>& operator=(spline<FpType, SplineType, Dimensions>&& other) = delete;

    spline& set_partitions( FpType* input_data, std::int64_t nx, partition_hint PartitionHint = partition_hint::non_uniform);
    spline& set_function_values(FpType* input_data, function_hint FunctionHint = storage_hint::row_major);
    spline& set_coefficients(FpType* data, coefficient_hint CoeffHint = storage_hint::row_major);
    bool is_initialized() const;
    std::int64_t get_required_coeffs_size() const;

    sycl::event construct(const std::vector<sycl::event>& dependencies = {});
    // for those types of splines where it's applicable
    spline& set_internal_conditions(FpType* input_data);
    spline& set_boundary_conditions(bc_type BCType = bc_type::free_end, FpType input_value = {});
};

Figure 4.  Spline Template Class
 

• There are two set functions that are only used for specific for types of splines: “set_internal_condition” and “set_boundary_condition.” If the spline doesn’t need to have internal and boundary conditions, then these functions are not needed.

Interpolate Function

Let us consider APIs for the “interpolate” function.

• Interpolant is a spline in most cases.
• If you need to calculate interpolation in a different SYCL queue, you can provide a queue as a 1^st parameter.
• Then we have memory and size for sites, memory for interpolation results.
• “der_indicator” is a bitset containing the number 1, if corresponding derivative order needs to be calculated. Only values are calculated if that parameter is not provided (no derivatives will be calculated).

template <typename Interpolant>
sycl::event interpolate(
    [sycl::queue& q,]
    Interpolant& interpolant,
    typename Interpolant::fp_type* sites,
    std::int64_t n_sites,
    typename Interpolant::fp_type* results,
    [std::bitset<32> der_indicator,]
    const std::vector<sycl::event>& dependencies = {},
    interpolate_hint ResultHint = interpolate_hint::funcs_sites_ders,
    site_hint SiteHint = site_hint::non_uniform);

Figure 5. Interpolation Function

• The last two parameters show the layout in which results should be placed, and uniformity of sites.

Next Steps and Your Feedback

Give it a try and let us know whether this approach to data fitting with cross-architecture supports using C++ interfaces meets your needs. This is a chance for you to help and shape the future of your favorite math kernel library.

Please also let us know any feature requests or suggestions you may have on our community forum. 

Get the Software

Test it for yourself today by downloading and installing the Intel® oneAPI  Base Toolkit

or just the Intel® onAPI Math Kernel Library. In addition to these download locations, they are also available through partner repositories. Detailed documentation is also available online.

Get Beta Access to New Intel® Technologies in the Cloud

If you would like to explore these tools in the cloud, sign up for an Intel® Developer Cloud account—a free development sandbox with access to the latest Intel® hardware and oneAPI software.

Starting right now, approved developers and customers can get early access to Intel technologies—from a few months to a full year ahead of product availability—and try out, test, and evaluate them on Intel’s enhanced, cloud-based service platform.

The beta trial includes new and upcoming Intel compute and accelerator platforms such as:

• 4th Gen Intel® Xeon® Scalable Processors (Sapphire Rapids)
• Intel® Xeon 4th Gen® processor with high bandwidth memory (HBM)
• Intel® Data Center GPU codenamed Ponte Vecchio
• Intel® Data Center GPU Flex Series
• Intel® Xeon® D processors (Ice Lake D),
• Habana® Gaudi®2 Deep Learning accelerators

Registration and prequalification is required.

Visit cloud.intel.com to get started.

See Related Content

Technical Articles

• Implement the Fourier Correlation Algorithm using DPC++ and oneMKL
• Accelerate R Code with Intel® oneAPI Math Kernel Library 
• Speed up Monte Carlo Simulations with Intel® oneAPI Math Kernel Library
• A Vendor-Neutral Path to Math Acceleration
• Migrating the HSOpticalFlow Estimation from CUDA* to SYCL* 

On-Demand Webinars

• Use oneMKL to Run Workloads in a Heterogeneous Environment
• Implement the Fourier Correlation Algorithm in a Few Lines of Code 
• Solve Enhanced Math Problems on GPUs with oneMKL