BASIC, Pascal, and C were the first programming languages that I learned, but I did my first serious coding (i.e., outside of a classroom) in Fortran. I used it almost exclusively for 12 years before switching to C and C++ when I joined Intel. I’ve lamented in some of my writings that I haven’t written a line of Fortran in 20 years. I was even starting to wonder if it was still relevant until my old pal Jim Cownie asked, “Is Fortran ‘A Dead Language?’”, and then answered convincingly that it isn’t. So, when a colleague asked me to try out the OpenMP* accelerator offload support in our latest Fortran compiler, I jumped at the chance.
You see, I like OpenMP as much as I like Fortran. It has always been an easy way to parallelize code, and the OpenMP specification has come a long way since it exploded onto the parallel computing scene in 1997. Today, it even supports accelerator offload. So instead of using SYCL, my usual language for accelerator offload, I’m going to return to my parallel programming roots to demonstrate how to offload computations to an accelerator using Fortran, OpenMP, and Intel® oneAPI Math Kernel Library (oneMKL).
The Experiment: Offloading LU Factorization to an Accelerator
If you’ve read some of my previous articles, you know that I like the Fourier correlation algorithm (article, webinar, code samples). I’ve used it in my biomolecular docking research and more recently for 2D and 3D image alignment. Since I’ve done this algorithm to death, I decided to do something different. Let’s see how easy it is to offload linear algebra computations (specifically, LU factorization) to an accelerator. An in-depth explanation of LU factorization is not the goal here. Suffice to say that it’s used to solve linear systems. If you want more details, the Intel® Math Kernel Library Cookbook has some good examples: Solving a System of Linear Equations with an LU-Factored Block Tridiagonal Coefficient Matrix and Factoring General Block Tridiagonal Matrices. I’m going to walk through a Fortran, oneMKL, and OpenMP implementation to illustrate the offload syntax and to highlight host-device data transfer in heterogeneous parallelism. I’ll start with the dgetri_oop_batch_strided.f90 example that’s included with oneMKL (see Using Code Examples), then modify it to improve efficiency.
The program begins by including the Fortran interfaces for OpenMP offload support, then it decides whether to use 32- or 64-bit integer type (see Using the ILP64 Interface vs. LP64 Interface for more information) (Figure 1). I’ll make this decision at compile-time, as shown in the compiler commands at the end of this article. To complete the setup, I set the number of matrices to factor and their sizes, set the dimension and stride parameters required by the oneMKL subroutines, and allocate the work arrays. We’re now ready to begin the calculation.
Figure 1. Setting up the example program. The oneMKL headers and modules that provide OpenMP target offload support are highlighted in blue. Note that the hardcoded matrix dimension and batch size parameters are fine for testing, but too small to merit acceleration.
The GPU that I have handy as I write this article only supports single-precision computations, so I’ll be using the Fortran REAL type and the appropriate LAPACK subroutines to compute the LU factorization (sgetrf_batch_strided) and out-of-place inversions of the LU-factored matrices (sgetri_oop_batch_strided). (Converting back to double-precision is a simple matter of switching to Fortran DOUBLE PRECISION type and using the LAPACK dgetrf_batch_strided and dgetri_oop_batch_strided subroutines.) The original example uses two OpenMP target data regions (Figure 2). The target construct transfers control to the device. The first region transfers the input matrices [map(tofrom:a)] to the device memory; dispatches the in-place LU factorization (sgetrf_batch_strided) to the device; and retrieves the LU-factored matrices (now stored in a), pivot indices [map(from:ipiv)], and status [map(from:info)] from device memory. If factorization succeeded, the program proceeds to the next OpenMP region. The LU-factored matrices and pivot indices are transferred back to the device memory [map(to:a) and map(to:ipiv)], the out-of-place inverses are computed on the device (sgetri_oop_batch_strided), and the inverses [map(from:ainv)] and status [map(from:info)] are retrieved from the device memory.
Figure 2 Offloading the LAPACK calculations to an accelerator using two OpenMP target regions, one for each LAPACK subroutine. OpenMP directives are highlighted in blue. LAPACK calls are highlighted in green.
The author of this example program may have used two OpenMP target regions to check the results of factorization before proceeding to inversion. The programmer’s caution is admirable, but it causes extra host-device data transfer, which is something we really want to avoid in heterogeneous parallel programming. Every arrowhead in Figure 3 represents data movement between disjoint memories. For example, the input matrices are transferred to the device, then the factors are transferred back to the host [map(tofrom:a)]. The same factors are then transferred back to the device [map(to:a)] in the next OpenMP target data region. Similarly, the pivot indices are retrieved from the device [map(from:ipiv)] after sgetrf_batch_strided returns, then transferred back to the device [map(to:ipiv)] for input to sgetri_oop_batch_strided. These matrices are presumably large if you’re going through the hassle of heterogeneous computing, so transferring them from host to device and vice versa could get expensive in terms of compute and power overhead. The one-dimensional status array is not that large, so I’m not as bothered by the map(from:info) transfer.
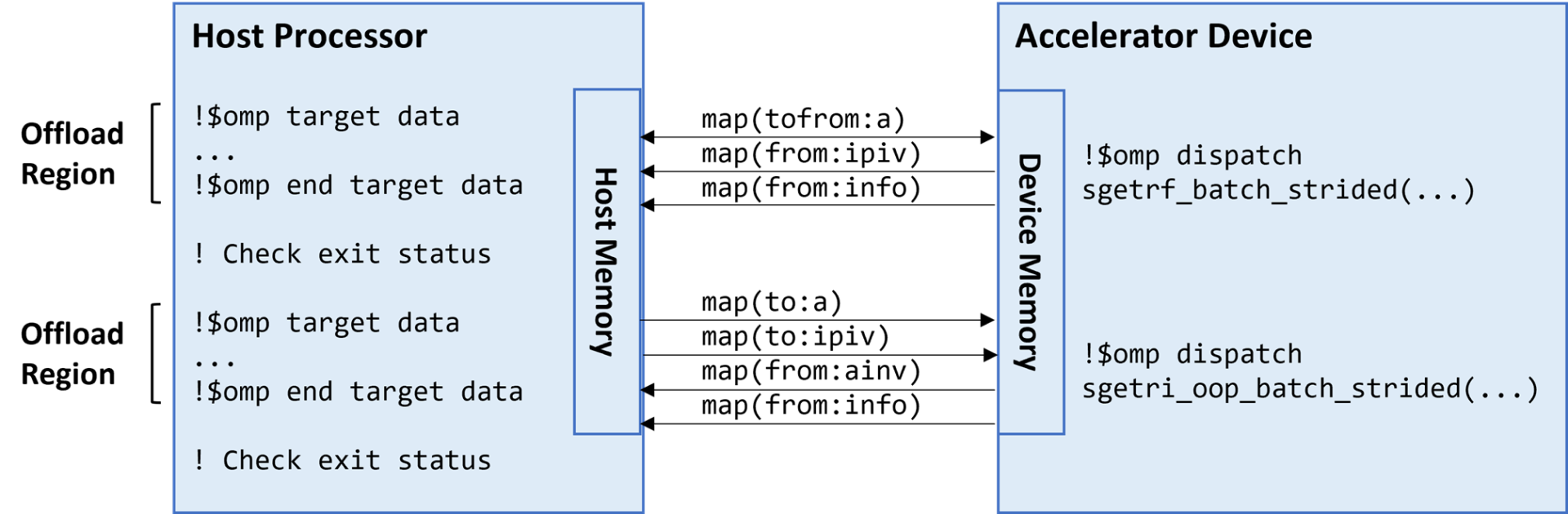
Figure 3 Host-device data transfer for the two OpenMP target offload regions shown in Figure 2. Each arrowhead indicates data movement between the host and device memories.
Ideally, the OpenMP runtime will check if the necessary data is already available in the device memory. However, there’s no guarantee that it won’t be flushed or overwritten between the OpenMP target regions. We also need to consider the overhead of creating two OpenMP offload regions. It’s better to do the entire computation in one offload region (Figure 4).
Figure 4 Offloading the LAPACK calculations to an accelerator using a single OpenMP target region. OpenMP directives are highlighted in blue. LAPACK calls are highlighted in green.
We can see that there’s less host-device data transfer when we fuse the two OpenMP target regions into one (Figure 5). The input matrices (a) are transferred to the device and factored in place. The LU factors and pivots (a, ipiv) computed by sgetrf_batch_strided on the device so they’re already in the device memory when sgetri_oop_batch_strided is called. We don’t need to transfer them back to the host unless we plan to use them later to solve a linear system. If that’s the case, however, we could just call sgetrs_batch_strided in the same OpenMP target data region while the necessary input data is already in device memory. I’ll leave that as an exercise for the reader.

Figure 5 Host-device data transfer for the OpenMP target offload region shown in Figure 4. Each arrowhead (except the one inside the accelerator device) indicates data movement between the host and device memories.
Try it Yourself
The example programs described in this article are available at this repository. They contain the code to initialize the input matrices and display the output from each step of the computation, which I did not include in this article. The commands to build the example programs using the Intel® Fortran Compiler and oneMKL, with and without OpenMP, are as follows:
The code is the same in either case, which highlights one of OpenMP’s main advantages. Namely, that it is non-invasive. The underlying serial code is still intact if the OpenMP directives are ignored by the compiler.
The oneMKL functions use SYCL methods to perform accelerator offload, so you have to install and configure device drivers and our Data Parallel C++ compiler along with the Intel Fortran Compiler and oneMKL. The easiest way to do this is to install both the Intel® oneAPI Base Toolkit and the Intel oneAPI HPC Toolkit. If you’re new to oneAPI or looking for updates, visit Intel® oneAPI Toolkits.
Note that the array dimensions and batch sizes shown in Figure 1 are fine for testing, but too small to benefit from acceleration. Computations should be large enough to amortize the overhead of transferring the control flow to the target device and transferring data between disjoint memories. I’ll cover the performance characteristics of the example code in a future article, but feel free to experiment with the array dimensions and batch sizes to get some idea of when it’s better to leave the computation on the host processor rather than offloading it to an accelerator.
I’ve only scratched the surface of OpenMP’s accelerator offload capability. There are many more offload constructs described in the OpenMP specification, but Intro to GPU Programming with the OpenMP API gives a gentle tutorial. You can experiment with OpenMP accelerator offload on the free Intel® Developer Cloud, which has the latest Intel® hardware and software.