This article was also published on oneAPI.io.
Story at Glance
- Old Dominion University and Fermi National Laboratory migrated the CUDA* code for the Parallel Adaptive GPU Algorithm for Numerical Integration (PAGANI) and m-Cubes algorithms to SYCL using the Intel® DPC++ Compatibility Tool.
- The SYCL code provided 90%-95% of the performance as a CUDA-optimized code on an NVIDIA* V100 Tensor Core GPU.
What are PAGANI and m-Cubes?
Numerical integration is necessary for many applications across various fields, especially physics. Important examples include beam dynamics simulation and parameter estimation in cosmological models. Even ill-behaving integrands (such as oscillatory and sharply peaked) can be efficiently integrated with modest computational resources as long the integration space is low dimensional (one or two variables). On the contrary, solving medium- to high-dimensional integrands is often infeasible on standard computing platforms. In such cases, we must execute on highly parallel architectures to achieve performance at scale.
PAGANI is a deterministic quadrature-based algorithm designed for massively parallel architectures. The algorithm computes an integral by evaluating the quadrature rules, a series of weighted summations. The computation involves an integrand function 𝑓,◻ which we invoke at the d-dimensional points 𝑥𝑖. Each point 𝑥𝑖. has a corresponding weight 𝑊𝑖 and there are \(f_{eval}\). such points in the summation. PAGANI computes an initial integral and error estimate, progressively improving its accuracy until it reaches a user-specified threshold. The accuracy improvement is achieved by applying the quadrature rules in small regions of the integration space and accumulating those values to get the integral estimate.
m-Cubes is a probabilistic Monte Carlo algorithm based on the VEGAS integrator. It operates by randomizing the sample generation across the integration space to solve integrands. It relies on the standard deviation of the Monte Carlo estimate to produce error estimates for the computation. Like VEGAS, m-Cubes uses importance and stratified sampling to accelerate the Monte Carlo convergence rate. The algorithm partitions the integration space into m subcubes that are sampled separately. A user-specified number of samples per iteration dictates the subdivision resolution.
Challenge of Vendor Lock-In
Without universally adopted standards, a viable solution for general portability relies on platform-agnostic programming models targeting multiple architectures via a unifying interface. This enables running a single code base across various architectures. Portability could only be achieved through the maintenance of multiple code bases.
Traditionally, the proprietary CUDA programming model has been the most popular but is exclusively targeted to NVIDIA GPUs. Parallel computing platforms such as GPUs are greatly suited for parallelizing numerical integration.
Unfortunately, exploration of execution-platform portability has been limited until recently in the context of parallel numerical integration libraries. To target both maximum performance and portability, we developed two SYCL implementations for the PAGANI and m-Cubes parallel algorithms, which we migrated from CUDA to enable performant and high-accuracy multidimensional integration across multiple architectures, including GPUs or multi-CPU configurations.
CUDA to SYCL Implementation for PAGNI and m-Cubes
The Intel® toolkits ecosystem provides a suite of compilers, libraries, and software tools (including the Intel DPC++ Compatibility Tool) that automate most of the porting process. SYCL, an organic extension of C++ standards, and the migration tools' capability to quickly port large CUDA implementations place the oneAPI programming model at the forefront of the portability initiative.
PAGANI and m-Cubes are iterative algorithms that offload most operations to an accelerator, as shown in the flowcharts of figures 1 and 2. This is done through library calls and custom implementations of parallel methods. Intel DPC++ Compatibility Tool automatically converts almost all Thrust library calls from the original CUDA implementation to SYCL equivalents.
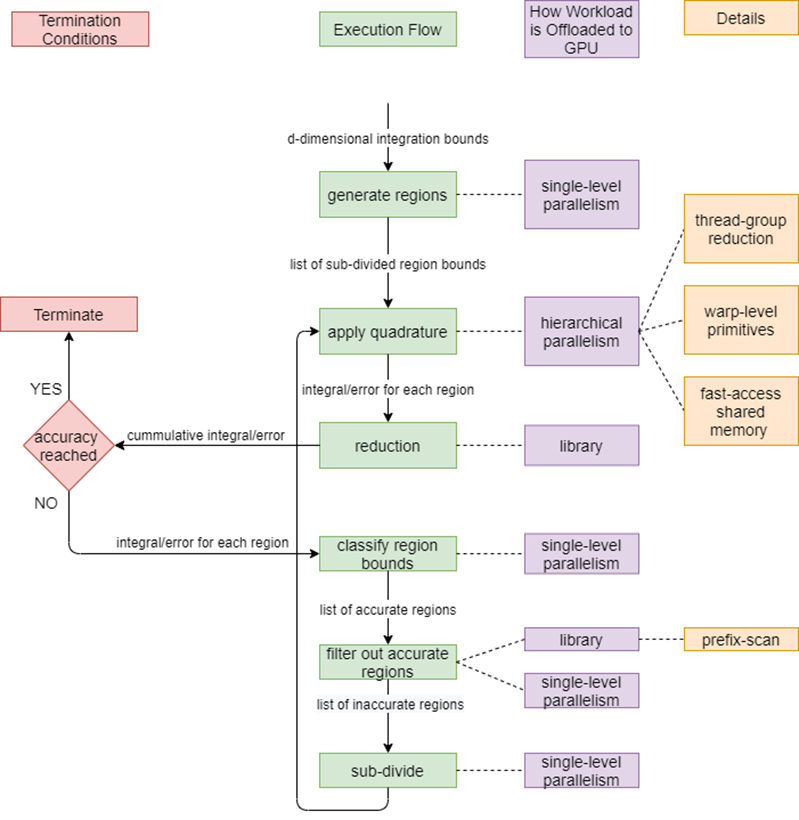
Figure 1. PAGANI flowchart
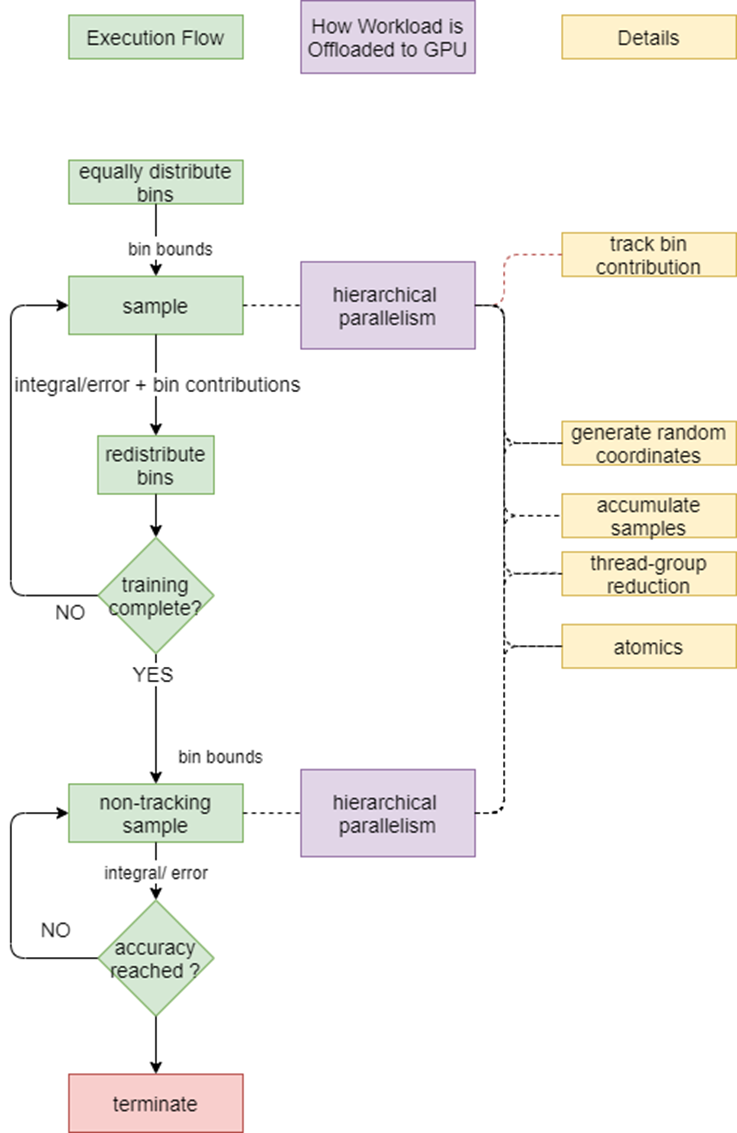
Figure 2. m-Cubes flowchart
The one exception was the minimax method where Intel DPC++ Compatibility Tool placed a warning indicating an incompatibility, as shown in figure 3. The library call conversion is a particularly useful feature since it allows the user to identify the appropriate library to use easily.
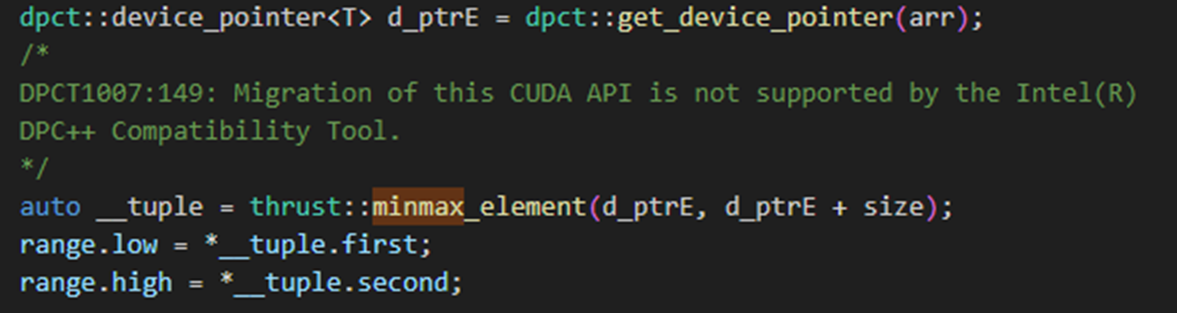
Figure 3. The case where Intel DPC++ Compatibility Tool did not successfully migrate a library call.
There were very few cases where Intel DPC++ Compatibility Tool migrated code needed minimal additional manual efforts to port the code. In one such scenario, the converted code caused a static assertation error. Figure 4 contains a simplified code based on the original CUDA implementation that causes the same error. Intel DPC++ Compatibility Tool replaces the call to the kernel method with a lambda expression that captures the variables in the same scope, which includes the region object. That object is just a collection of memory addresses for data used in the kernel. Since the object is not trivially copyable, it causes a compilation error in SYCL. The code must be adapted to bring individual pointers to those addresses into scope instead of a struct containing them to correct it. The result of figure 5 is more verbose but is fully functional.
Note: regions->leftcoord cannot be used directly in the lambda expression as it would lead to an illegal access runtime error.
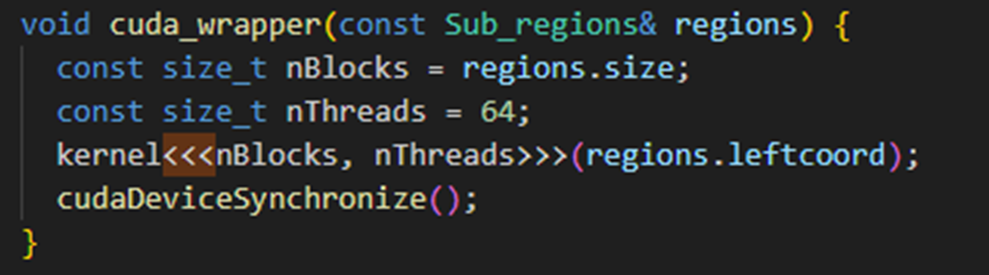
Figure 4. Example of a kernel call that Intel DPC++ Compatibility Tool does not properly convert.
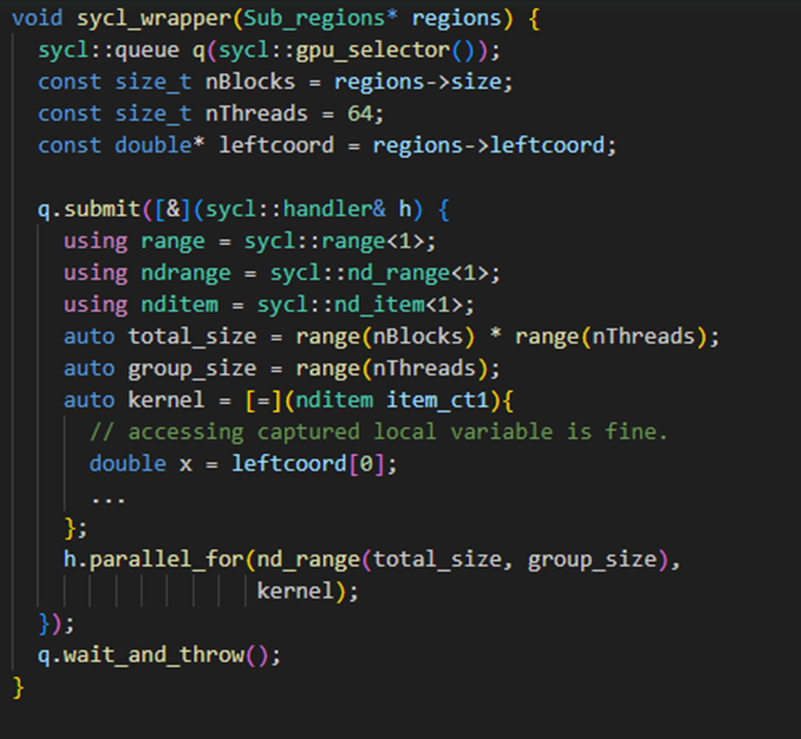
Figure 5. Example of functional SYCL code based on the CUDA code of figure 4.
Performance Evaluation
To properly capture the performance of the integrators, we evaluated the main kernels of PAGANI and m-Cubes with many different input values. We used two types of integrands. First, we ran the following functions, typically used to evaluate numerical integration algorithms.
\(f_{1,d} (x)= cos(\sum_{i=1}^{d}ix_i)\)
\(f_{2,d} (x)= \Pi_{i=1}^{d}(\frac{1}{50^2}+(x_i-0.5))^{-1}\)
\(f_{3,d} (x)= (1+\sum_{i=1}^{d}ix_i)^{-d-1}\)
\(f_{4,d} (x)= exp(-625\sum_{i=1}^{d}(x_i - .5)^2)\)
\(f_{5,d} (x)= exp(-10\sum_{i=1}^{d}|x_i - .5)|)\)
\(f_{6,d} (x)= \begin{cases} (exp\sum_{i=1}^{d}(i+4)x_i) \text{ if } x_i < (3+i)/10\\ \quad \quad \quad \quad \quad0 \text{ otherwise } \end{cases} \)
Each integrand was run 10 times on the PAGANI and m-Cubes kernels for all dimensionalities between five and eight. The number of thread blocks used to launch the kernels varied to address different degrees of computational intensity.
Figures 6 and 7 show relatively small performance penalties of the oneAPI ports for each integrand. Inclusion of an addition function in the form of: f(x,d)=∑di=1xi allows the inspection of the performance of the kernels, providing an opportunity for optimizing the mathematical computations within complicated functions. After increasing the inline threshold to 10,000, we observed a significant performance improvement apart from m-Cubes, which was slower due to not using efficient atomic instructions.
After a few minor optimizations, the SYCL implementation of m-Cubes performance achieves 95% of its CUDA version, and the PAGANI SYCL implementation performance achieves 90%, as shown in figures 6 and 7.
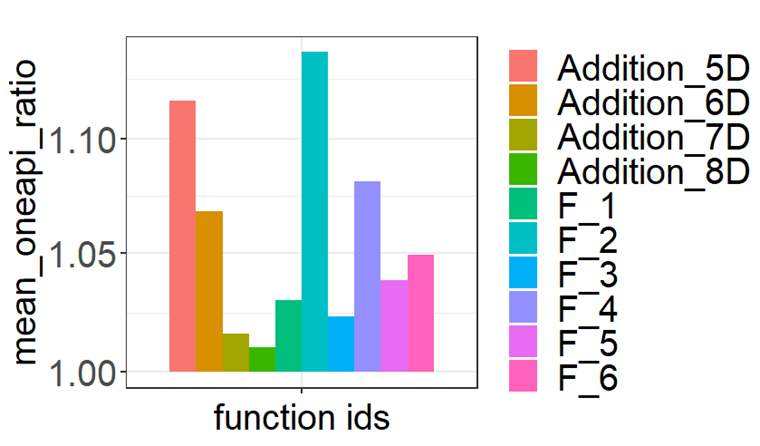
Figure 6. Average performance penalty of the oneAPI implementation of the main PAGANI kernel. Each bar on the x-axis corresponds to a different input function. The y-axis represents the ratio of runtimes \(\frac{sycl}{cuda}\) for each input. Results include functions of dimensionalities in the range of five to eight.
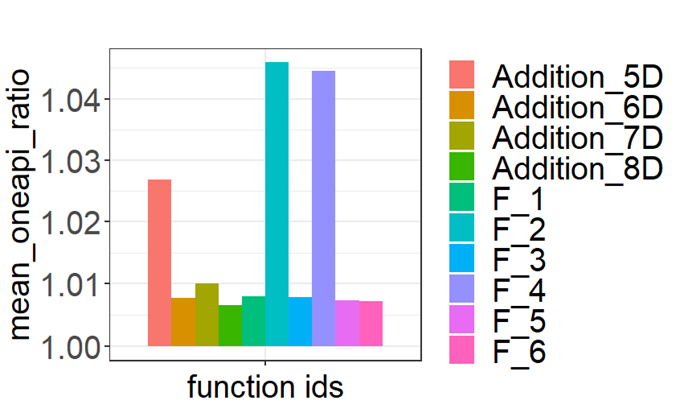
Figure 7. Average performance penalty of the oneAPI implementation of the main m-Cubes kernel. Each bar on the x-axis corresponds to a different input function. The y-axis represents the ratio of execution times \(\frac{sycl}{cuda}\) for each input. Results include functions of dimensionalities in the range of five to eight.
We observed a correlation between the number of extra registers and the performance penalty of the oneAPI implementation for PAGANI. As illustrated in figure 8, the largest performance penalties are observed for the "f2" and "f4" and 5D "Addition" integrands, which all have the most additional registers per thread.
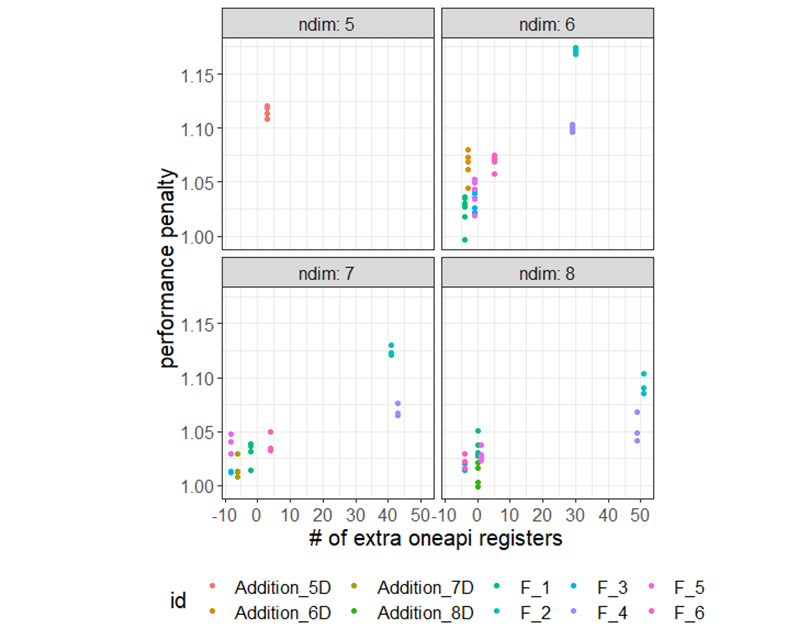
Figure 8. The correlation between allocated registers per thread and performance penalty. The x-axis represents the number of additional registers per thread allocated for the oneAPI implementation of the PAGANI kernel compared to the CUDA version. The y-axis represents the ratio of execution times \(\frac{sycl}{cuda}\) for each input.
For m-Cubes, we also see that the integrands with large register-count differences were slower than the others. The "f2" and "f4" integrands both have the larger register-count difference and the largest performance penalty. However, both integrands are faster when the dimensionality is higher, despite the register-count difference being larger in these cases as well.
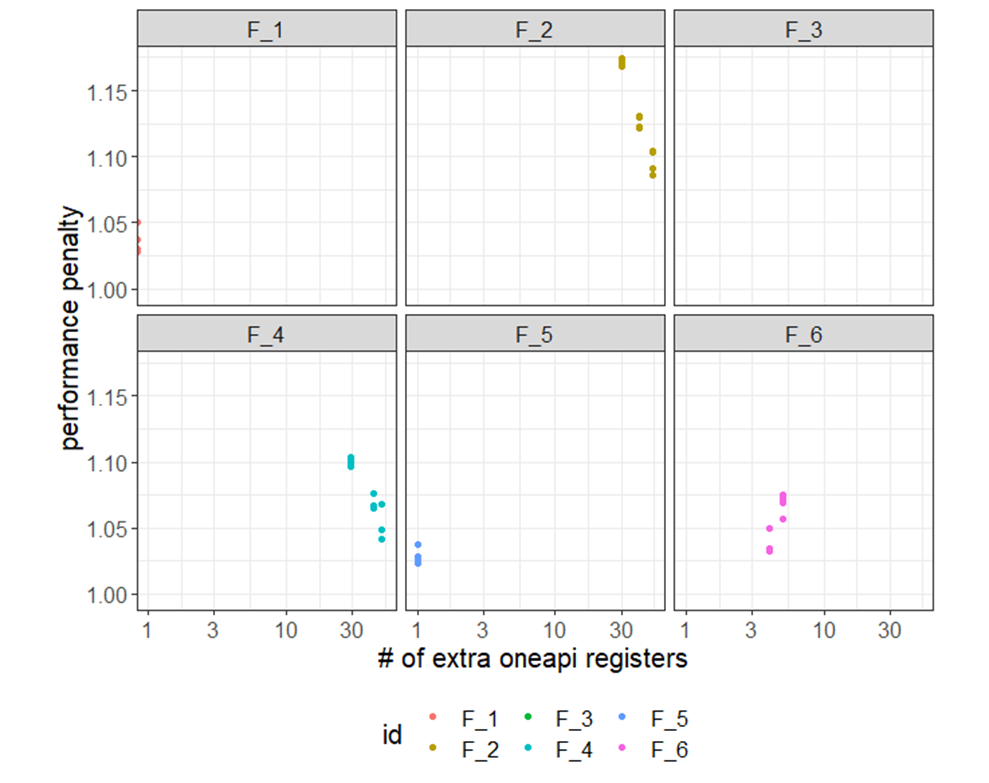
Figure 9. Register count differences (x-axis) and performance penalty (y-axis) for m-Cubes.
This demonstrated that our oneAPI ports perform comparably to the original CUDA implementations. As such, we expect that running on Intel GPUs that are more powerful than the integrated graphics Intel® HD Graphics P630 will yield comparable performance to CUDA on NVIDIA GPUs.
Testing Date: Performance results are recorded from experiments conducted on September 1, 2023. Intel does not control or audit third-party data. You should consult other sources to evaluate accuracy.
Configuration Details and Workload Setup: Intel® Xeon® Gold 6130, 2.10 Ghz CPU, Tesla V100-SXM2 GPU. Comparing compilers: NVCC 11.6.124, Clang 15.0.0. PAGANI and m-Cubes configuration, input-function dimensionality: [3,8]. Number of regions to process for PAGANI: [512, 19487171], number of samples for m-Cubes: [108, 3∙10^9].
- Numerical Integration on GPUs
- Ran performance metrics on NVIDIA v100 GPU
- Ran successfully on a P630 GPU from Intel
Conclusion
By using the Intel DPC++ Compatibility Tool, we accelerated the transition of our numerical integration CUDA implementations to oneAPI. We observed that the assigned registers per thread can deviate between oneAPI and CUDA codes, which may cause performance degradation due to its effect on thread use. Despite any performance deviations, we demonstrated that there is only minimal performance penalty when transitioning from CUDA to oneAPI. The performance of oneAPI is equivalent when the kernel-launch configurations have similar thread use. After extended development efforts, the vast array of libraries, ease of portability, and small margin of performance degradation make oneAPI and Intel toolkits an appropriate software solution for numerical integration use cases.