Visible to Intel only — GUID: GUID-958FB333-18A1-40E2-96C5-8DE7E511FAE0
Visible to Intel only — GUID: GUID-958FB333-18A1-40E2-96C5-8DE7E511FAE0
heevd (USM Version)
Computes all eigenvalues and, optionally, all eigenvectors of a complex Hermitian matrix using divide and conquer algorithm. This routine belongs to the oneapi::mkl::lapack namespace.
Description
The routine computes all the eigenvalues, and optionally all the eigenvectors, of a complex Hermitian matrix A. In other words, it can compute the spectral factorization of A as: A = Z*Λ*ZH.
Here  is a real diagonal matrix whose diagonal elements are the eigenvalues
is a real diagonal matrix whose diagonal elements are the eigenvalues 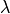 i, and Z is the orthogonal matrix whose columns are the eigenvectors zi. Thus,
i, and Z is the orthogonal matrix whose columns are the eigenvectors zi. Thus,
A*zi = λi*zi for i = 1, 2, ..., n.
If the eigenvectors are requested, then this routine uses a divide and conquer algorithm to compute eigenvalues and eigenvectors. However, if only eigenvalues are required, then it uses the Pal-Walker-Kahan variant of the QL or QR algorithm.
API
Syntax
namespace oneapi::mkl::lapack {
sycl::event heevd(sycl::queue &queue,
mkl::job jobz,
mkl::uplo uplo,
std::int64_t n,
T *a,
std::int64_t lda,
T *w,
T *scratchpad,
std::int64_t scratchpad_size,
const std::vector<sycl::event> &events = {})
}
heevd (USM version) supports the following precision and devices.
T |
Devices Supported |
|---|---|
std::complex<float> |
CPU and GPU |
std::complex<double> |
CPU and GPU |
Input Parameters
- queue
-
Device queue where calculations will be performed.
- jobz
-
Must be job::novec or job::vec.
If jobz = job::novec, then only eigenvalues are computed.
If jobz = job::vec, then eigenvalues and eigenvectors are computed.
- uplo
-
Must be uplo::upper or uplo::lower.
If upper_lower = job::upper, a stores the upper triangular part of A.
If upper_lower = job::lower, a stores the lower triangular part of A.
- n
-
The order of the matrix A (0 ≤ n).
- a
-
The pointer to the array containing A, size (lda,*). The second dimension of a must be at least max(1, n).
- lda
-
The leading dimension of a. Must be at least max(1,n).
- scratchpad
-
Pointer to scratchpad memory to be used by the routine for storing intermediate results.
- scratchpad_size
-
Size of scratchpad memory as a number of floating point elements of type T. Size should not be less than the value returned by the heevd_scratchpad_size function.
- events
-
List of events to wait for before starting computation. Defaults to empty list.
Output Parameters
- a
-
If jobz = job::vec, then on exit this is overwritten by the orthogonal matrix Z which contains the eigenvectors of A.
- w
-
Pointer to array of size at least n. Contains the eigenvalues of the matrix A in ascending order.
Exceptions
Exception |
Description |
|---|---|
mkl::lapack::exception |
This exception is thrown when problems occur during calculations. You can obtain the info code of the problem using the info() method of the exception object: If info = -i, the i-th parameter had an illegal value. If info = i, and jobz = job::novec, then the algorithm failed to converge; i indicates the number of off-diagonal elements of an intermediate tridiagonal form which did not converge to zero. If info = i, and jobz = job::vec, then the algorithm failed to compute an eigenvalue while working on the submatrix lying in rows and columns info/(n+1) through mod(info,n+1). If info is equal to the value passed as scratchpad size, and detail() returns non zero, then the passed scratchpad has an insufficient size, and the required size should not be less than the value returned by the detail() method of the exception object. |
Return Values
Output event to wait on to ensure computation is complete.