3. Fronthaul Compression IP Functional Description
Compression and Decompression
A preprocessing block-based bit shift block generates the optimum bit-shifts for a resource block of 12 resource elements (REs). The block reduces the quantization noise, especially for low-amplitude samples. Hence, it reduces the error vector magnitude (EVM) that compression introduces. The compression algorithm is almost independent of the power value. Assuming the complex input samples is x = x1 + jxQ, the maximum absolute value of the real and imaginary components for the resource block is:
The maximum value of the resource block n is:
Having the maximum absolute value for the resource block, the following equation determines the left shift value assigned to that resource block:
Where bitWidth is the input bit width.
The IP supports compression ratios of 8, 9, 10, 11, 12, 13, 14, 15, 16.
For a compression ratio of 16 (udCompParam field = 0, according to the O-RAN WG specification), the IP does not perform compression or decompression.
Mu-Law Compression and Decompression
The algorithm uses Mu-law companding technique, which speech compression widely uses. This technique passes the input uncompressed signal, x, through a compressor with function, f(x), before rounding and bit-truncation. The technique sends compressed data, y, over the interface. The received data passes through an expanding function (which is the inverse of the compressor, F-1(y). The technique reproduces the uncompressed data with minimal quantization error.
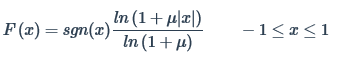
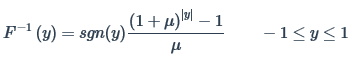
The Mu-law IQ compression algorithm follows the O-RAN specification.
Digital Power Scaling
IQ power level in dB full scale (dBFS) is a logarithmic representation of the power level for an IQ sample carried over the digital interface. IQ power level in dBFS is proportional to logarithm of I²+Q²:
IQ power level [dBFS] = 10·log10( I²+Q² ) - 10·log10(FS)
= 10∙log10 (I²+Q² ) - 10∙log10(FS 0 × 2-FS_Offset )
where:
- I is the in-phase portion of a received constellation point;
- Q is the quadrature portion of a received constellation point;
- FS is the full scale (maximum) permitted value of I or Q based on their digital representations;
- FS_Offset is an M-plane parameter (value 0 if this parameter is not supported by O-RU or not set by O-DU);
- FS 0 = max(I²) = max(Q²) = max(I²+Q²) with max over all IQ values that can be represented by IQ data format in U-plane message.
The actual IQ values that may occur in a U-plane message are restricted by
I²+Q² ≤ FS = FS 0 ×∙ 2(-FS_Offset)
For frequency domain IQ data, 0 dBFS is the maximum power level that one subcarrier can carry over. The smallest non-zero IQ power level is defined by the interface resolution.
O-RU normalizes any received DL value to its internal representation of full scale so that a 0 dBFS can be properly processed.
Example 1:
FS_Offset = 0
I = min I, Q = 0
With 9-bit mantissa 2's complement + 4-bit exponent compression: min I = -256 × 215 = -223
FS 0 = 246, FS = FS 0 2-FS_Offset = 246
0 dBFS is equivalnet to the average(I²+Q²) = 246
Interface resolution is the equivalent to 1/(246), which is the equivalent to -138.47 dBFS
Example 2:
FS_Offset=10
I=min I, Q=0
With 14-bit mantissa 2's complement + 4-bit exponent compression: min I = -213 × 215 = -228, which is the erquivalent to
FS 0 = 256, FS = FS 0 × 2-FS_Offset = 256-10 = 246
0 dBFS is the erquivalent to average(I²+Q²) = 246
Interface resolution is the erquivalent to 1/(246) is the erquivalent to -138.47 dBFS
Digital power scaling is supported for block floating point compression and decompression. You can set the FS Offset values through the IP registers. The FS Offset values can be from 0 to 15. The decompression and compression values are scaled value of square root FS Offset for decompression and compression.
| FS OFFSET | Decompression value | Compression value |
| 0 | 128 | 32,768 |
| 1 | 181 | 23,170 |
| 2 | 256 | 16,384 |
| 3 | 362 | 11,585 |
| 4 | 512 | 8,192 |
| 5 | 724 | 5,792 |
| 6 | 1,024 | 4,096 |
| 7 | 1,448 | 2,896 |
| 8 | 2,048 | 2,048 |
| 9 | 2,896 | 1,448 |
| 10 | 4,096 | 1,024 |
| 11 | ,5793 | 724 |
| 12 | 8,192 | 512 |
| 13 | 11,585 | 362 |
| 14 | 16,384 | 256 |
| 15 | 23,170 | 181 |